基于人工势场法的智能车辆动态避障研究

张 涌，黄林雄，张 煜，吴海啸，姜朋昌

ZHANG Yong, HUANG Linxiong, ZHANG Yu, WU Haixiao, JIANG Pengchang

（南京林业大学 汽车与交通工程学院，江苏 南京210037）

(College of Automobile and Traffic Engineering, Nanjing Forestry University, Nanjing 210037, China)

0 引 言

随着社会经济发展，国内汽车保有量不断增加，汽车安全问题不断涌现出来。面对不断增加的汽车安全问题，国内外人士一致认为发展无人驾驶汽车是解决安全问题的有效途径。作为无人驾驶汽车领域内核心技术之一——避障路径规划得到越来越多的关注。

现阶段，比较常见的局部路径规划算法有遗传算法[1]、模糊逻辑算法[2]、神经网络算法[3]、人工势场法[4]。Khabit 等人提出了应用于机器人避障领域的人工势场法[5]，通过模拟电子在磁场中受到的引力势场和斥力势场的作用，实现机器人行进路线的规划，与其他路径规划算法相比，人工势场法具有结构简单、实时性好、生成的路径圆滑等优点[6—8]，但是在路径规划过程中未考虑车辆动力学和运动学的约束以及道路边界的约束；翼杰等建立了实际道路交通环境下的动态三维危险势场模型[9]，但是该模型只解决了在静态障碍物作用下的避障路径规划；曹昊天等提出了在障碍车辆前方和后方建立引导势场的方法[10]，从而建立了弹性绳模型，实现车辆超车避障，但是该方法并不能实现车辆及时回到原车道的中心。在路径跟踪控制方面，比较常见的有模型预测控制[11]、预瞄控制[12-13]、PID 控制[14]、前馈—反馈控制[15]等方法。其中，预瞄控制和模型预测控制得到广泛的应用。预瞄控制虽然引入车辆动力学特性，并且保留了预瞄控制鲁棒性强的特点，但是车辆动力学对车辆的影响随着速度的改变而改变。当车辆以较低车速行驶时，车辆动力学约束对于车辆影响较小，但是随着车速的提高，车辆动力学约束对车辆的影响越大，预瞄控制无法保证车辆在各种工况下的安全性和稳定性。所以，路径跟踪控制器需要全面地考虑车辆非线性动力学约束和执行机构的极限约束[16]，而模型预测控制面对多约束系统具有明显的优势。

因此，本文借鉴传统人工势场法的思想，构造基于道路环境的人工势场模型，为了解决无人驾驶车辆动态避障的要求，将避障过程分成若干时间片段T，在每个时间片段T内对避障路径不断地进行优化，同时，本文基于模型预测控制理论设计所需的路径跟踪控制器，跟踪由上述改进人工势场法得出的避障路径，CarSim/Simulink 联合仿真结果证明本文改进的人工势场法能够安全有效地躲避障碍物，并且本文设计的路径跟踪控制器具有良好的跟踪效果。

1 改进的人工势场模型

图1 大地坐标系

为了方便建立人工势场法的数学模型，建立如图1 所示的大地坐标系，规定纵向道路的长度方向为X方向，道路的宽度方向为Y方向。

同时，为了实现车辆的动态避障，本文将避障路径规划的整个过程分成若干个时间片段T，在时间片段T内假设障碍车辆从C匀速直线运动到C'的位置，无人驾驶车辆（以下简称为自车） 从A运动到A'的位置，终点目标从B匀速直线运动到B'的位置，如图2 所示。在下一个时间片段T内，自车从A'点出发，重复上述过程，直到自车完成避障。

图2 时间片段T 内车辆规划的路径

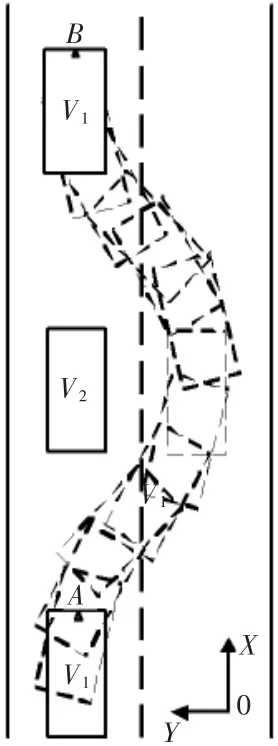
图3 位置关系图

1.1 引力势场模型

根据经验可知，车辆在正常行驶或者在完成转向回到正常行驶状态时，车辆一般位于车道的中间。所以，本文以车辆需要完成避障地区域D内车道中点作为引力势场终点。位置关系如图3 所示，假设图3 中的A点为避障的起点，B点为避障的终点，V1为自车，V2为障碍车辆。

根据前文的假设，自车在区域D中完成避障，因此要求在此区域中引力势能朝着终点方向减小，所以本文建立的引力势场函数如下所示：

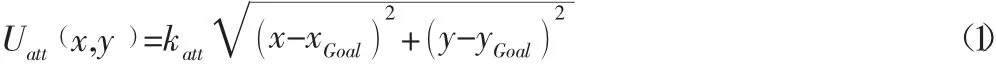
式中：katt为引力势能增益系数；为终点的位置坐标；（x,y）为自车的位置坐标；由式（1） 可得到不同位置下的引力势能分布，如图4 所示。

1.2 障碍物斥力势场模型

在人工势场法中，距离决定了障碍物斥力势场对自车的影响程度，当自车进入障碍物斥力势场作用域内时，两者之间的距离越小，自车受到的斥力越大；反之，自车受到的斥力越小。当自车离开障碍物斥力势场的作用域时，自车受到的斥力为零。所以，本文建立的斥力势场函数如下：

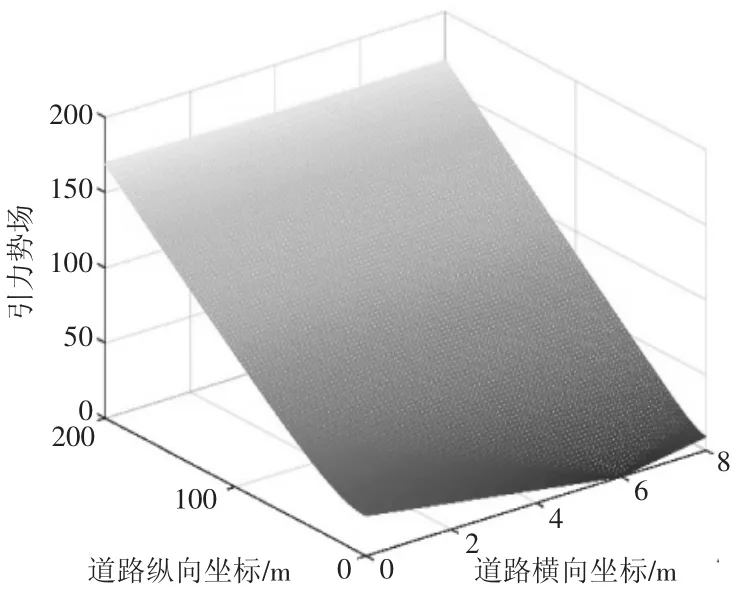
图4 引力势能三维分布图

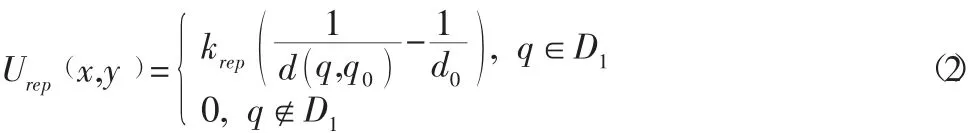
式中：krep为斥力势能增益系数；q=f x,（y）为自车或者障碍物的位置坐标；d q,（q0）为自车与障碍物之间的距离；d0为障碍物斥力势场作用域D1能影响的最大距离。

实际行驶过程中，由于车辆受到自身性能、道路环境的限制以及车辆横向与纵向速度不同，所以障碍物斥力势场作用域D1与传统机器人避障时的圆形作用域不同。因此，本文对斥力势场的作用域D1作了如下改进：将D1的纵向距离增大，使自车能够提前修正方向，进入避障模式；将D1的横向距离减小，保证自车能够安全地进行避障。经过修改后的作用域D1变成了椭圆形，如图5 所示。

本文中斥力势场作用域D1的长轴L1由障碍物的危险程度决定[17]，即：

图5 斥力势场作用域

式中：α 为障碍物的危险程度；Dmin为最小安全距离。

短轴L2为障碍物边缘（靠近避障一侧） 到车道线的距离，假设车辆在车道中间行驶，则：

式中：β 为安全因子；H为避障的目标车道与原车道几何中心线的间距；c为障碍物的宽度。

为了解决传统人工势场法中目标不可达和局部最优的问题，本文引入了斥力势场调节因子ρg，只有当车辆到达避障终点时，斥力和引力同时减小为零。综上所述，经过对斥力势场函数（2） 的修改，得到新的斥力势场函数为：

1.3 道路边界势场模型

车辆不同于机器人，车辆在道路上行驶时，在考虑障碍物的同时需要考虑道路对于车辆的约束。由驾驶经验可知，道路边界区域是危险系数最高的区域，道路中线区域次之，车道中线区域则是危险系数最小的区域。根据上述的道路危险程度分布情况，分段考虑道路边界势场函数。当车辆位于两条车道线之间的区域时，采用变化趋势比较平缓的函数；而在其他区域时，由于危险系数较高，因此采用变化趋势较大的函数。以双车道为例，综合上述因素，建立的道路边界势场函数为：

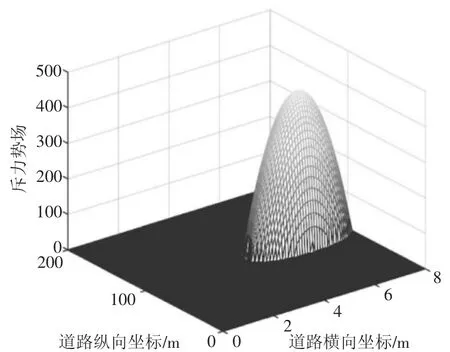
图6 斥力势场三维分布图

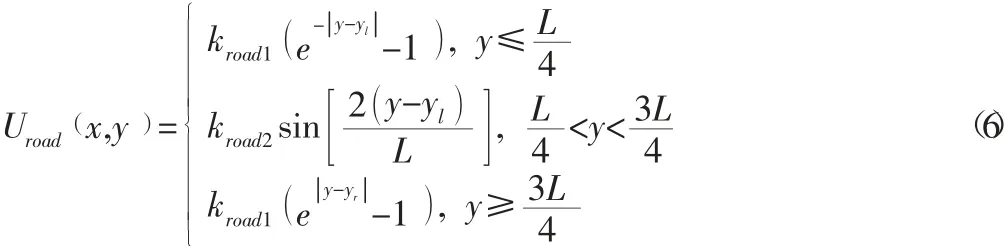
式中：kroad1、kroad2为道路边界势能增益系数；yl、yr为左右车道中心线的横向位置；L为道路宽度。由式（6） 得到不同位置下道路边界势能分布，如图7 所示。

综上所述，车辆在避障区域中行驶时总势场为终点引力势场、障碍物斥力势场和道路边界势场的和，其数学表达式为：

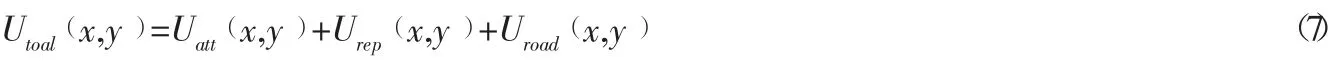
总势场的三维分布如图8 所示。

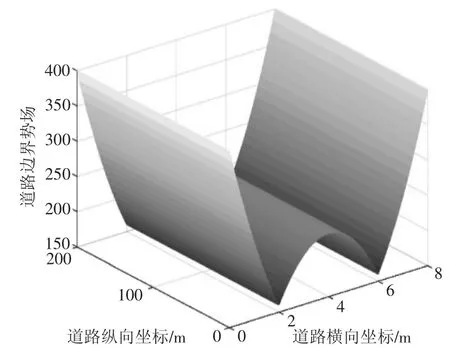
图7 道路边界势场三维分布图

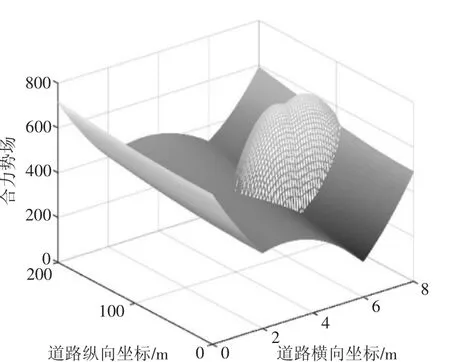
图8 总势场三维分布图

2 基于模型预测控制的路径跟踪控制器设计

2.1 车辆动力学模型

本文设计的路径跟踪控制器是为了能够让车辆较好地跟踪规划的避障路径，同时能够降低模型的复杂程度，因此，选用能够较好描述车辆转向特性的单轨模型来描述车辆运动。建立的车辆模型为三自由度车辆模型即只考虑了车辆的纵向、横向、横摆运动，车辆动力学模型如图9 所示。

结合所搭建的车辆模型和牛顿第二定律，建立车辆模型运动学微分方程，具体表述如下：

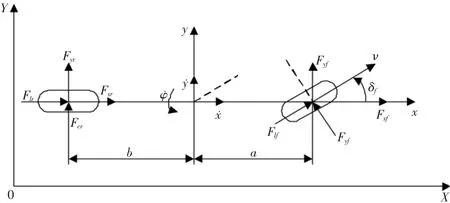
图9 三自由度车辆模型

式中：Flf、Flr分别为车辆前轮轮胎和后轮轮胎受到的纵向力；Fcf、Fcr分别为车辆前轮轮胎和后轮轮胎受到的侧向力；δf为车辆前轮转角；φ 为车辆横摆角；IZ为车辆绕Z轴的转动惯量；a为车辆前轴到质心的距离；b为车辆后轴到质心的距离。

不考虑轮胎非线性特性，根据汽车理论[18]的内容，引入轮胎侧偏刚度、纵向刚度、侧偏角、滑移率，则轮胎的侧偏力可以表示为：

式中：Clf、Clr为车辆前轮和后轮轮胎的纵向刚度；Ccf、Ccr为车辆前轮和后轮轮胎的侧偏刚度；Sf、Sr为车辆前轮和后轮轮胎的滑移率。

为了后续简化计算，假设车辆的轮胎侧偏角和前轮转角的数值较小，则：

综上所述，本文建立的车辆动力学模型为：

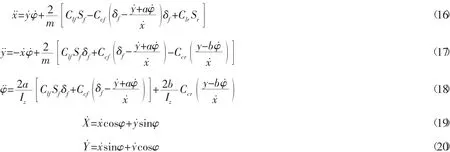
2.2 路径跟踪控制器设计

本文设计的路径跟踪控制器基于模型预测控制理论[19-20]，经过推导，可以得到线性化和离散化后的状态方程：

模型预测控制设计过程中的目标函数为：

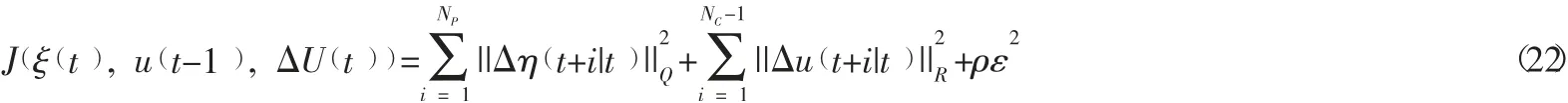
式中：NP为预测时域；NC为控制时域；为实际输出与参考路径之差；为避障路径规划所得；ρ 为权重系数；ε 为松弛因子；Q、R为权重矩阵。

为了求解式（22），将式（21） 转化为：

因此，新的状态空间表达式为：

根据上述目标函数并结合车辆在避障过程中受到的车辆自身性能和道路环境限制，需要满足以下基本约束条件：

控制量约束：

控制增量约束：

软约束：

除了上述的基本约束条件，为了保证在避障过程中车辆的稳定性和舒适性，需要引入车辆动力学的约束，主要为车辆质心侧偏角约束和附着条件约束。根据BOSH 公司的车辆稳定性研究结果[21]，将质心侧偏角和附着条件约束设置为：

式中：ay,min、ay,max为车辆横向加速度最小值和最大值；ε 为松弛因子。

在每个控制周期内，系统根据上述的约束条件，对目标函数（22） 求解，得出的结果为控制时域内的一系列包含控制增量和松弛因子的控制序列[22]，其中的第1 个元素作为实际的控制增量作用于系统。通过不停的循环，在每个控制周期内重复上述过程，最终实现车辆对规划的避障路径进行跟踪。

3 仿真实验分析

本文的仿真实验通过CarSim 软件和Simulink 联合仿真实现。联合仿真模型如图10 所示。

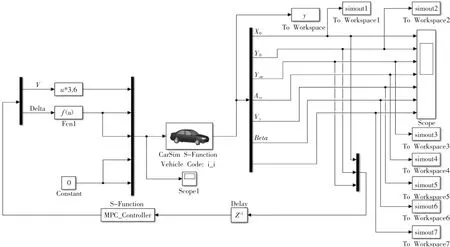
图10 CarSim/Simulink 联合仿真

假设自车在双车道上行驶，路况满足横向避障的要求，自车的车速为80km/h，障碍车辆车速为40km/h，车道宽为4m，自车初始位置为（0,6），障碍车辆位置为（50,6），初始终点位置为（100,6）。根据前文改进的人工势场法，对车辆进行避障路径规划，结果如图11 所示，路径跟踪效果如图12 所示。

图11 避障路径规划结果图

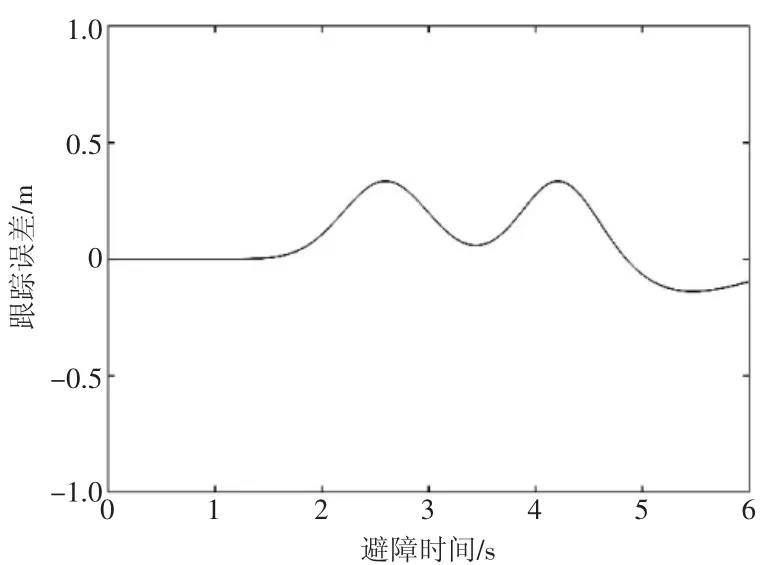
图12 路径跟踪效果图

从图11 和12 中可以得出，自车与障碍车辆的横向距离大于2m，与道路边界的距离接近于3.5m，远大于自车车身宽度的一半，说明本文改进的人工势场法能够安全有效地避开障碍物。并且本文设计的基于模型预测控制理论的路径跟踪控制器能够有效地完成对路径跟踪的任务，其跟踪误差在0.35m 之内。

图13 为车辆避障过程中的横摆角速度变化曲线，从图13 中可以看出车辆的横摆角速度在-0.25rad/s 到0.16rad/s 之间，曲线变化平滑且连续，并不存在突变和震荡的情况，说明自车在避障过程中具有较好的稳定性。

图14 为车辆的质心侧偏角变化曲线。从图14 中可以得出自车的质心侧偏角在-0.24°到0.48°以内，满足前文所述的-12°≤β≤12°约束条件，进一步证明了本文提出的结合模型预测控制的改进人工势场法能够在小误差跟踪期望轨迹的前提下，保持较好的车辆稳定性。

4 总 结

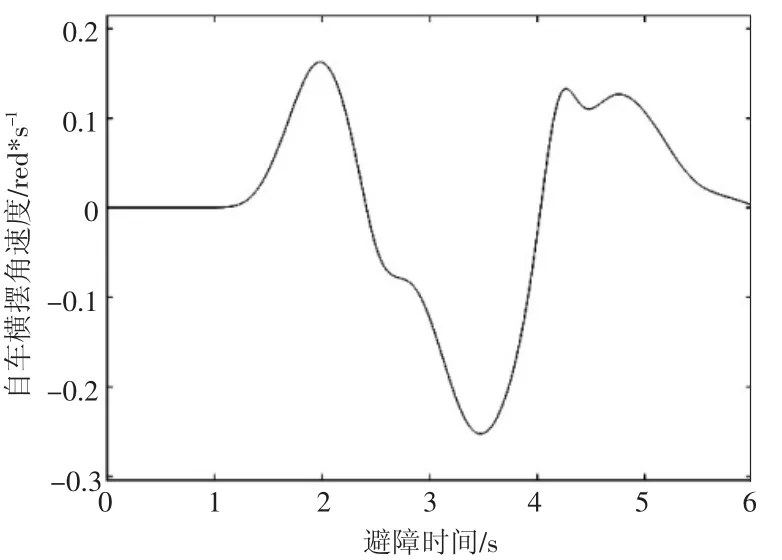
图13 自车横摆角速度曲线

图14 自车质心侧偏角变化曲线

本文基于改进的人工势场法提出了一种适用于无人驾驶车辆的动态避障算法，并且基于模型预测控制理论，设计了所需的路径跟踪控制器，对上述改进人工势场法得出的避障路径进行跟踪。CarSim/Simulink 联合仿真结果表明：经过本文改进的人工势场法得出的避障路径具有实时性良好、且平顺安全的特点。同时，自车的横摆角速度和质心侧偏角在避障过程中都处于规定的范围之中，曲线平滑连续，进一步体现了自车在路径规划与跟踪过程中的稳定性，大大提高了自车行驶的安全性。