车联网仿真实验平台搭建与参数校正研究

林晓辉，徐建闽，魏文钰，梁逸龙，蔡立椿

LIN Xiaohui1, XU Jianmin2, WEI Wenyu1, LIANG Yilong1, CAI Lichun1

（1. 广东交通职业技术学院 轨道交通学院，广东 广州510650；2. 华南理工大学 土木与交通学院，广东 广州510640）

(1. Institute of Rail Traffic, Guangdong Communication Polytechnic, Guangzhou 510650, China; 2. School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510640, China)

0 引 言

近年来，随着WAVE、DSRC、5G 以及WiMAX 等通信技术的不断发展，在不久的将来，城市中的大部分车辆将相互连接，形成“交通实体”与“信息主体”紧密结合的超级网络，即车联网环境[1-2]。车联网将大大地提升城市交通的安全性和通行效率[3]，是各国智能交通发展路线图中的关键环节。目前车联网的研究主要集中在车联网技术体系、车联网信息交互技术、车联网与交通工程交叉领域理论和技术问题、车联网环境下基于虚拟现实技术的交通流演化分析方法等4 个方面[4]，但车联网尚处于实验研究阶段，通过搭建真实车联网环境来验证各种实验研究的难度较大且成本较高。鉴于此，本文选取广州市实际路网作为实验区域，利用Vissim 交通仿真软件，给出了车联网仿真实验平台的具体搭建过程。

另一方面，由于Vissim 软件的模型默认参数是依据德国道路交通条件来设置的，不一定适合我国道路交通运行情况，因此，有必要对车联网仿真实验平台的模型参数进行校正。目前用于仿真模型参数校正的算法有正交试验法[5]、遗传算法（Genetic Algorithm，GA）[6-8]、同步扰动随机逼近算法（Simultaneous Perturbation Stochastic Approximation，SPSA）[9-10]、人工萤火虫算法（Glowworm Swarm Optimization，GSO）[11]、人工蜂群算法（Artificial Bee Colony Algorithm，ABC）[12]等。上述算法均有优缺点，比如正交试验算法简捷、易用，但校正参数过多时，操作起来比较繁琐。简单遗传算法消耗时间长，收敛速度慢，容易陷入局部最优，部分学者利用群体智能算法改善简单遗传算法局部搜索效率低的问题，但这类混合算法局部寻优计算相对复杂，较大限制了参数优化效率[13]。SPSA 算法对大规模数据搜索时具有优势，对于仿真模型参数校正而言，其校正参数个数有限，其优势反而未能充分发挥。GSO 算法需要计算大量个体之间的距离，会影响其运行速度。人工峰算法易陷入“过早”收敛，得到局部最优解。因此，本文结合本平台的实际情况，将采用正交试验法对车联网仿真实验平台的模型参数进行校正。

1 车联网仿真实验平台搭建

1.1 路网基础数据

（1） 路网布局情况

实验区域为广州市天河区核心路网交叉口群，其路网平面布局图通过百度地图放大后，直接截图拼接，形成高清的路网布局图。各路段车道数通过查看百度街景地图后，确定各路段车道数，形成各路段车道数统计表。取城市道路标准车道宽度3.25m 作为仿真平台的单车道宽度。同样通过查看百度街景地图后，统计得到交叉口平面布局。

（2） 路网交通流量数据

以广州SCATS 交通信号控制系统在某个早高峰小时所检测交通数据为主，人工调查的个别交叉口早高峰小时流量为辅，经统计得到各交叉口的流量情况，经整理后得到路网的边界入口流量。

（3） 交叉口信号控制方案

大部分交叉口信号控制方案由广州市智能交通指挥中心提供，个别交叉口信号方案采用实地人工调查所得，最后经数据整理得到路网的各交叉口信号控制方案情况表。

1.2 仿真实验平台搭建流程

依上述路网基础数据，利用Vissim4.3 交通仿真软件搭建车联网仿真实验平台，其具体步骤如下：（1） 导入广州天河区核心路网交叉口群布局图；

（2） 选择某条路段，将其放大至最大，按车道宽度设置比例尺；

（3） 按照车道布局情况、交叉口布局情况，绘制路网拓扑结构；

（4） 在路网边界路段设置驶入交通流量，将全部车辆定义为浮动车，即构建了车联网环境。为了模拟路网从低峰到高峰的整个过程，定义仿真时刻32 400s 为高峰时刻，每隔1 小时，按13.5%递减路网边界驶入交通量，直至3 600s。

（5） 依据所调查的交叉口信号控制方案和交通流量高峰、平峰、低峰的变化，设置各交叉口多时段信号控制方案，无信号交叉口设置减少让行控制。

（6） 在转弯处设置减速度，在各交叉口设置停车排队检测器、旅行时间检测器、在各路段中间设置数据采集检测器。

（7） 为了获取各路段的交通数据，在Evaluation—Files—link Evaluation—Configuration 中设置路段参数，如采集数据时间间隔（Simulation Time）、路段编号（Link Number）、路段速度（Speed）、路段密度（Density）、路段起讫点XY 坐标、路段长度（Length） 等，如图1 所示。

通过设置各路段的检测区域，可获取路段参数。双击每条路段，弹出对话框Link Data，点击按键Other→Evaluation，然后弹出对话框Link Evaluation，将路段实际长度输入到Segment Length（路段评价长度） 中，如图2 所示。

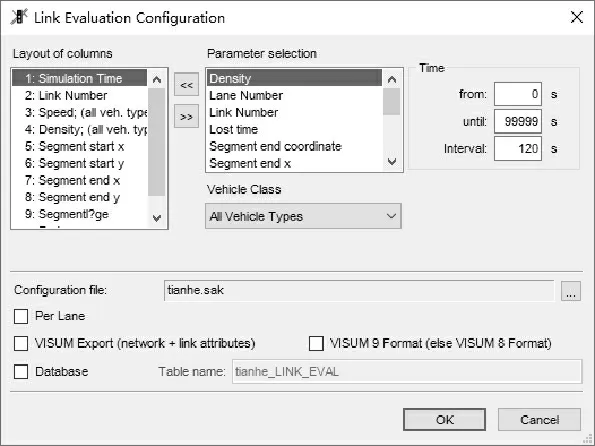
图1 仿真模型中获取路段参数设置

图2 设置各路段评价长度

仿真结束后，在*.str 文件中得到各路段相关交通数据，其各列数据代表意义如表1 所示。

（8） 通过数据采集检测器可获取各路段的交通参数，在Vissim4.3 中选择Evaluation—Files—Data Collection—Configuration功能，在弹出的对话框中，点击Auto（Groups），然后将各数据检测器所属的编号修改为所在的路段编号，如图3 所示。

仿真结束后，在*.mes 文件中可得数据采集器数据， 其各列数据代表意义如表2 所示。

（9） 通过Evaluation—Files—Vehicle Record—Configuration 功能，可模拟车联网环境。每辆联网车状态数据获取间隔时间为15s，状态数据包括Simulation Time（采集时间）、Vehicle Number（车辆编号）、Link Number（所在路段编号）、Speed（速度）、World Coordinate FrontX（车头X坐标位置）、World Coordinate FrontY（车头Y坐标位置），如图4 所示。

仿真结束后，在*.fzp 文件中可得到每辆联网车状态数据，其各列数据代表意义如表3 所示。

最终搭建车联网仿真实验平台，如图5 所示。

表1 *.str 文件的数据格式及意义

表2 *.mes 文件的数据格式及意义

表3 .fzp 文件的数据格式及意义

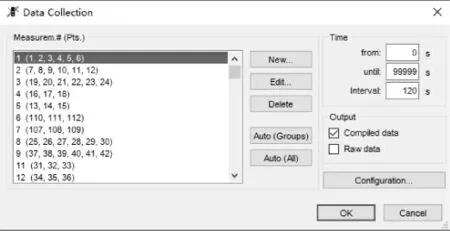
图3 数据检测器所在路段编号设置

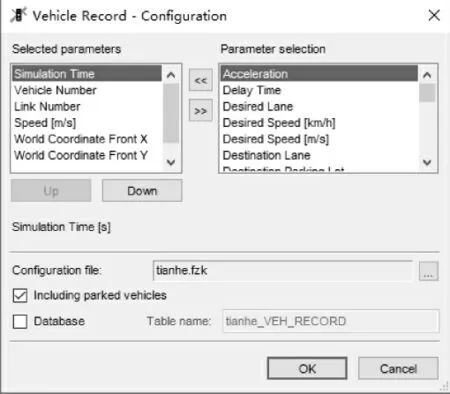
图4 联网车状态数据设置

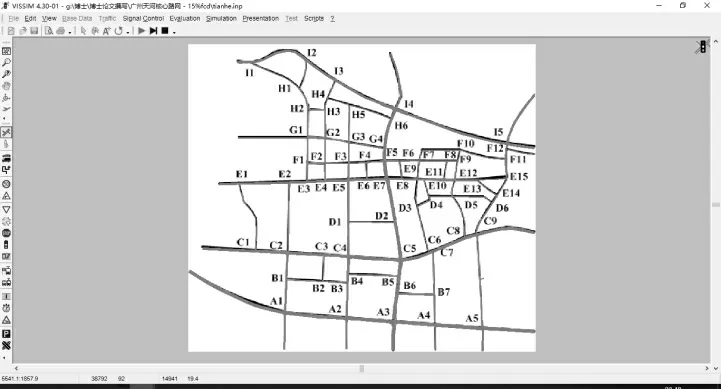
图5 车联网仿真实验平台

2 车联网仿真实验平台参数校正

2.1 参数校正流程

本文将采用基于正交试验法的仿真模型参数标定方法[5]，对车联网仿真实验平台参数进行校正，其具体流程如图6 所示。

（1） 确定参数校正目标

选择路网各边界入口实际流量和仿真流量的平均绝对相对误差（Mean Absolute Percent Error，MAPE） 最小为校正目标，MAPE越小，则仿真模型的效果越好，反之，效果越差，其公式如下：式中：n为路网边界入口总数；i为仿真路网的第i个边界入口；为仿真路网的第i个边界入口实际交通流量，为仿真路网的第i个边界入口仿真流量交通，veh/h。

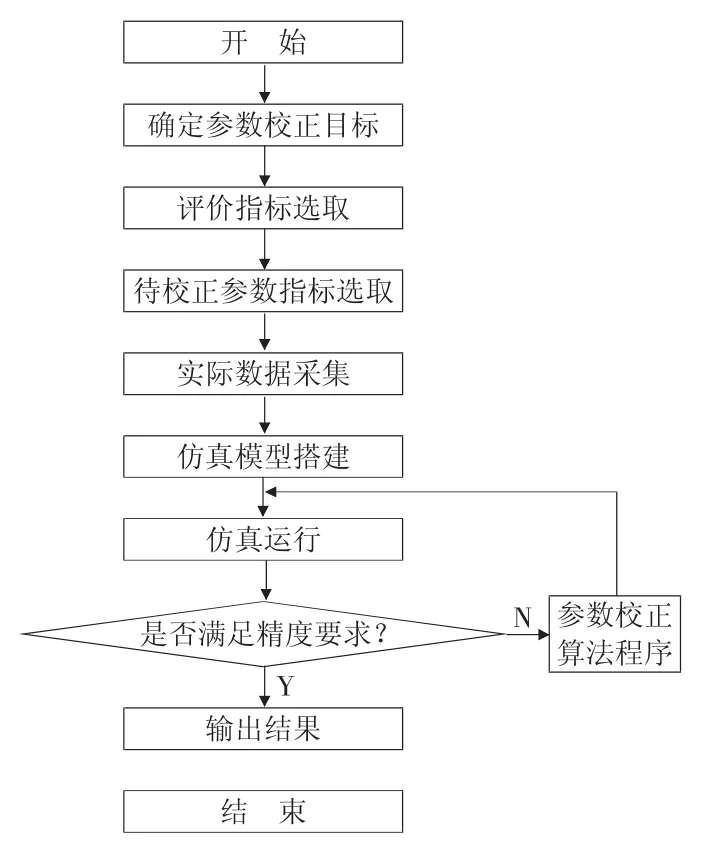
图6 仿真模型参数校正流程

（2） 确定待校正参数及步长

研究表明，前方可观察车辆数、平均停车间距、安全距离附加部分、安全距离倍数部分、最小车头空距和消除前的等待时间等6 个参数是影响仿真模型结果的主要参数[5]。因此，选择此6 个参数作为待校正参数，其默认值及取值范围如表4 所示。

6 个参数依据取值范围和步长，可分别划分为5 个取值，如前方可观察车辆数的取值，可用a1,a2,a3,a4,a5表示。

（3） 设计合适的正交表

依据正交试验法，不考虑各参数之间交互作用，将各参数随机安排在正交表各列上，如表5 所示。

（4） 仿真试验，并记录仿真结果

依据试验方案表，修改仿真模型的参数，分别运行各试验方案，并将每套试验方案的仿真结果（即路网边界入口的MAPE值） 记录在表5 中，如Y2表示采用第2 套试验方案后，仿真路网各边界入口的MAPE值。

编号 参数名称 默认值 取值范围 步长 编号 参数名称 默认值 取值范围 步长a 前方可观察车辆数 2.0 1～5 1.0 d 安全距离倍数部分 3.0 2～4 0.5 b 平均停车间距 2.0 1～3 0.5 e 最小车头空距 0.5 0.5～2.5 0.5 c 安全距离附加部分 2.0 1～3 0.5 f 消除前的等待时间 60.0 30～90 15.0

方案号 a b c d e f Y 方案号 a b c d e f Y 1 a1 b1 c1 d1 e1 f1 Y1 14 a3 b4 c1 d3 e5 f2 Y14 2 a1 b2 c2 d2 e2 f2 Y2 15 a3 b5 c2 d4 e1 f3 Y15 3 a1 b3 c3 d3 e3 f3 Y3 16 a4 b1 c4 d2 e5 f3 Y16 4 a1 b4 c4 d4 e4 f4 Y4 17 a4 b2 c5 d3 e1 f4 Y17 5 a1 b5 c5 d5 e5 f5 Y5 18 a4 b3 c1 d4 e2 f5 Y18 6 a2 b1 c2 d3 e4 f5 Y6 19 a4 b4 c2 d5 e3 f1 Y19 7 a2 b2 c3 d4 e5 f1 Y7 20 a4 b5 c3 d1 e4 f2 Y20 8 a2 b3 c4 d5 e1 f2 Y8 21 a5 b1 c5 d4 e3 f2 Y21 9 a2 b4 c5 d1 e2 f3 Y9 22 a5 b2 c1 d5 e4 f3 Y22 10 a2 b5 c1 d2 e3 f4 Y10 23 a5 b3 c2 d1 e5 f4 Y23 11 a3 b1 c3 d5 e2 f4 Y11 24 a5 b4 c3 d2 e1 f5 Y24 12 a3 b2 c4 d1 e3 f5 Y12 25 a5 b5 c4 d3 e2 f1 Y25 13 a3 b3 c5 d2 e4 f1 Y13

（5） 极差分析

通过极差分析，得到同一模型参数的不同取值对评价指标的影响程度及各参数的影响程度主次顺序，从而确定最优参数组合，如表6 所示。

参数 a b c d e f 参数 a b c d e f K1 ΣYa1 ΣYb1 ΣYc1 ΣYd1 ΣYe1 ΣYf1 K 2 m ΣYa2 1 1 m ΣYb2 1 m ΣYc2 1 m ΣYd2 1 m ΣYe2 1 m ΣYf2 K2 ΣYa2 ΣYb2 ΣYc2 ΣYd2 ΣYe2 ΣYf2 K 3 m ΣYa3 1 1 m ΣYb3 1 m ΣYc3 1 m ΣYd3 1 m ΣYe3 1 m ΣYf3 K3 ΣYa3 ΣYb3 ΣYc3 ΣYd3 ΣYe3 ΣYf3 K 4 m ΣYa4 1 1 m ΣYb4 1 m ΣYc4 1 m ΣYd4 1 m ΣYe4 1 m ΣYf4 1 K4 ΣYa4 ΣYb4 ΣYc4 ΣYd4 ΣYe4 ΣYf4 m ΣYa5 1 m ΣYb5 1 m ΣYc5 1 m ΣYd5 1 m ΣYe5 1 m ΣYf5 K5 ΣYa5 ΣYb5 ΣYc5 ΣYd5 ΣYe5 ΣYf5 R Ra Rb Rc Rd Re Rf K 5 K 1 m ΣYa1 1 1 m ΣYb1 1 m ΣYc1 1 m ΣYd1 1 m ΣYe1 1 m ΣYf1

在表6 中，Ki表各参数的第i个取值对应的评价指标之和。比如c参数的K2表示c参数取值c2时，对应的Y之和，即

R表示某个参数的极差，即某个参数的最大值与最小值之差，其公式如下：

极差反映了评价指标的变化幅度，依据极差，可以判别各参数变化对评价指标的影响程度。极差越大，说明该参数变化对评价指标的影响越大，该参数越重要。

（6） 确定参数主次及最优取值

（7） 校验最优参数组合

依据最优参数组合，设置仿真模型参数，重新进行仿真，验证评价指标是否满足精度要求（≤5%），若满足精度要求，则结束参数校正，否则返回第2 步骤，重新设计参数取值表和正交方案表，继续进行参数校正，直到满足精度要求。

2.2 参数校正结果

依据正交试验算法，对车联网仿真实验平台参数进行校正，其具体流程如下：

（1） 默认参数仿真结果分析

采用默认参数，进行仿真，得到0～3 600s 时仿真路网边界入口的仿真流量，与路网各边界入口的实际流量做对比，得到MAPE值，如表7 所示。默认参数下路网边界入口的MAPE超过5%，不满足精度要求，因此需要对仿真模型的参数进行校正。

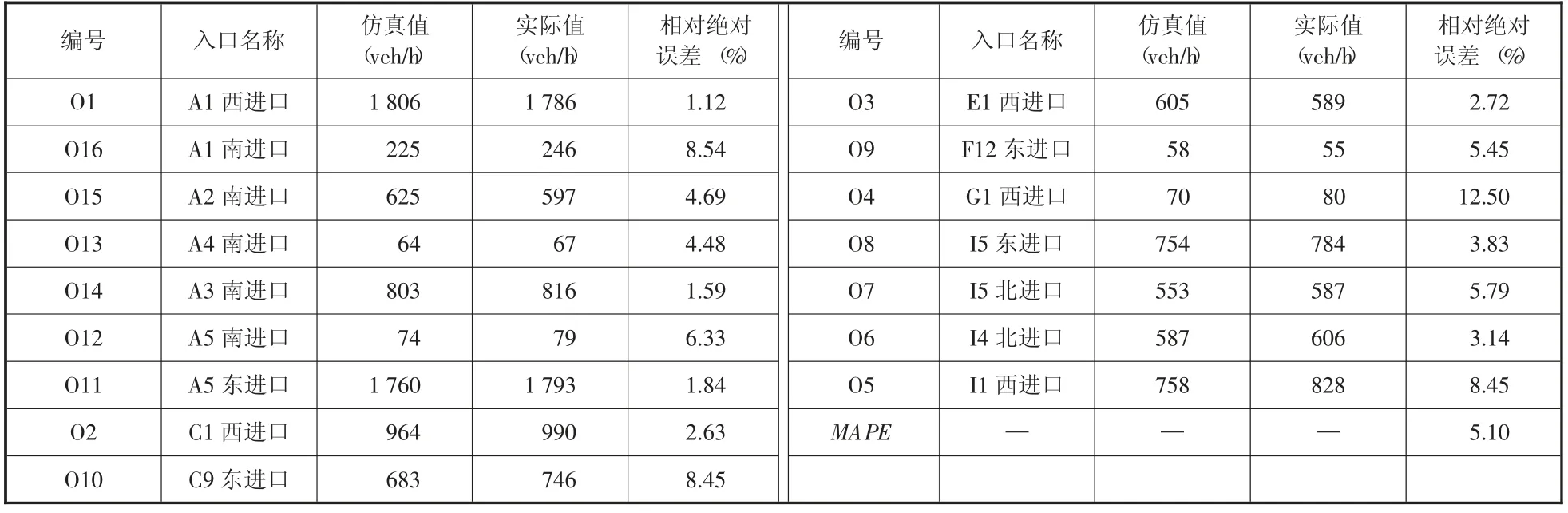
表7 默认参数仿真结果分析（0～3 600s）

（2） 确定参数取值表

依据表4 中各参数的取值范围和步长，将各参数划分为5 个取值，确定参数取值如表8 所示。

表8 车联网仿真实验平台参数取值表

（3） 设计正交试验方案表

依据表5 内容，设计本平台的正交试验方案，如表9 所示。

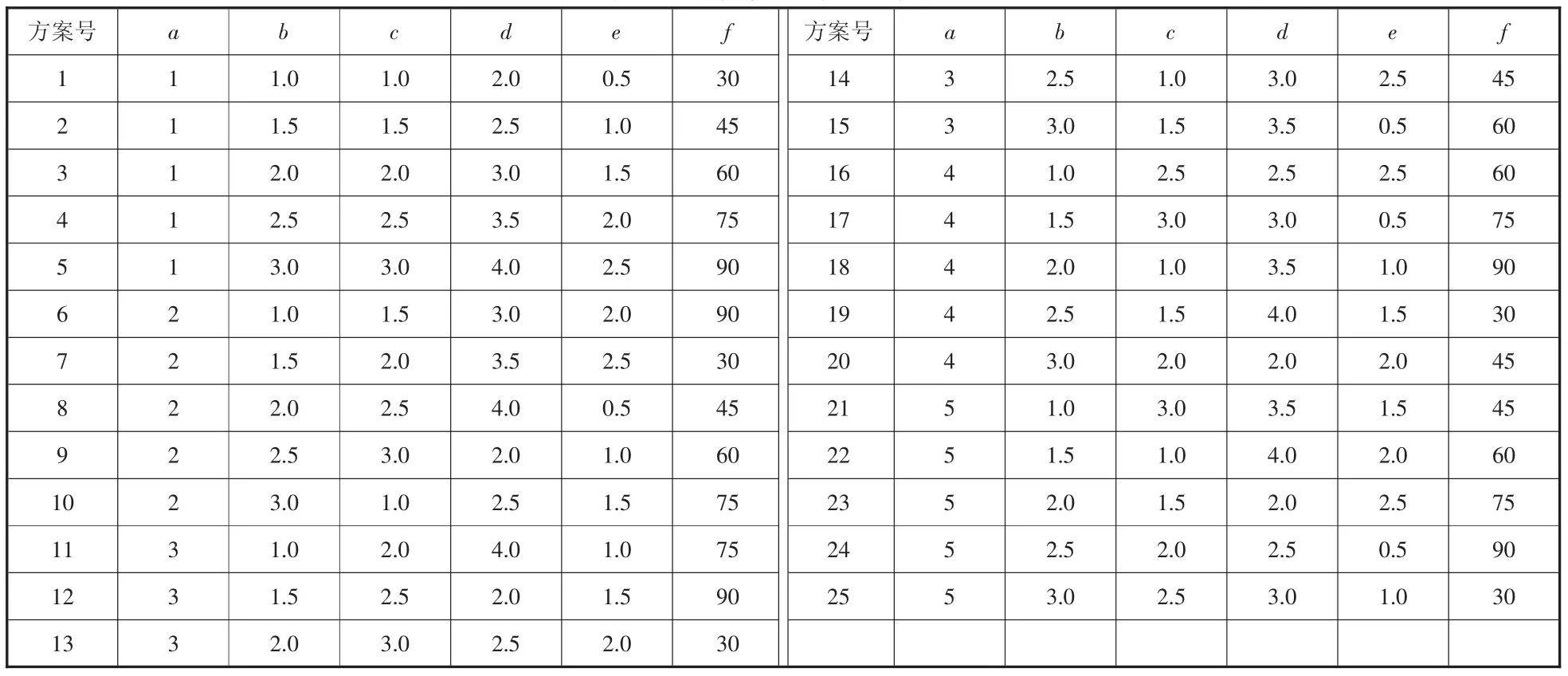
表9 车联网仿真实验平台正交试验方案

（4） 列出试验结果

依据表9 的25 套试验方案，分别设置仿真模型参数，然后运行仿真平台，依据仿真数据可整理得到各试验方案的路网边界入口流量的MAPE，如表10 所示。

（5） 极差分析，确定最优解

依据表6 计算得到车联网仿真实验平台的参数极差分析表，如表11 所示。按照极差值从大到小，确定参数主次排序：febcad。以各参数的取值为X坐标，对应的为Y坐标，绘制各参数与的趋势图，如图7 所示。选择误差最小的对应参数值为最优参数值，得到最优参数组合为f1,e3,b4,c4,a4,d3，即f=30，e=1.5，b=2.5，c=2.5，a=4，d=3。

（6） 验证最优组合

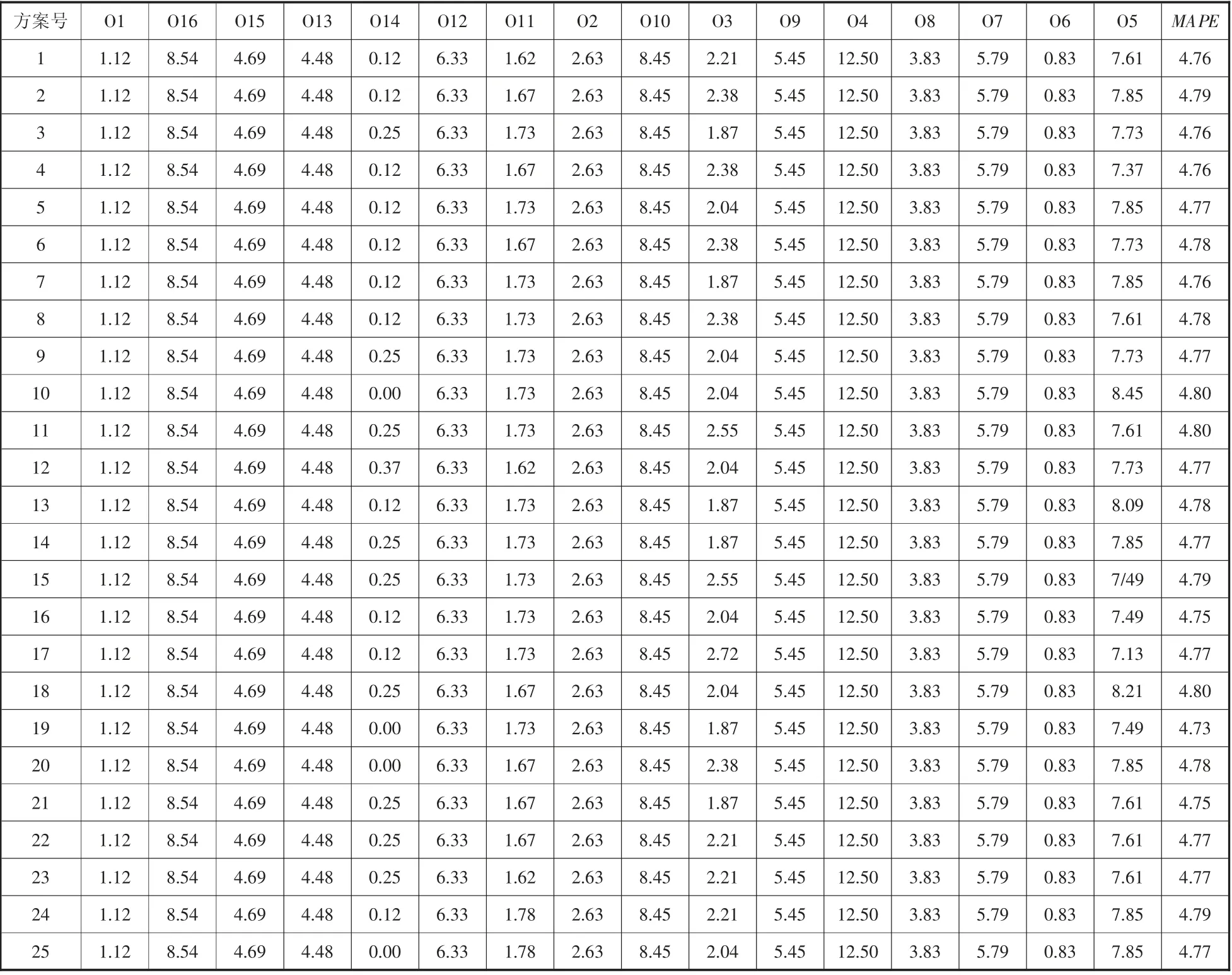
表10 各正交试验方案下路网边界入口流量的MAPE 值 单位：%

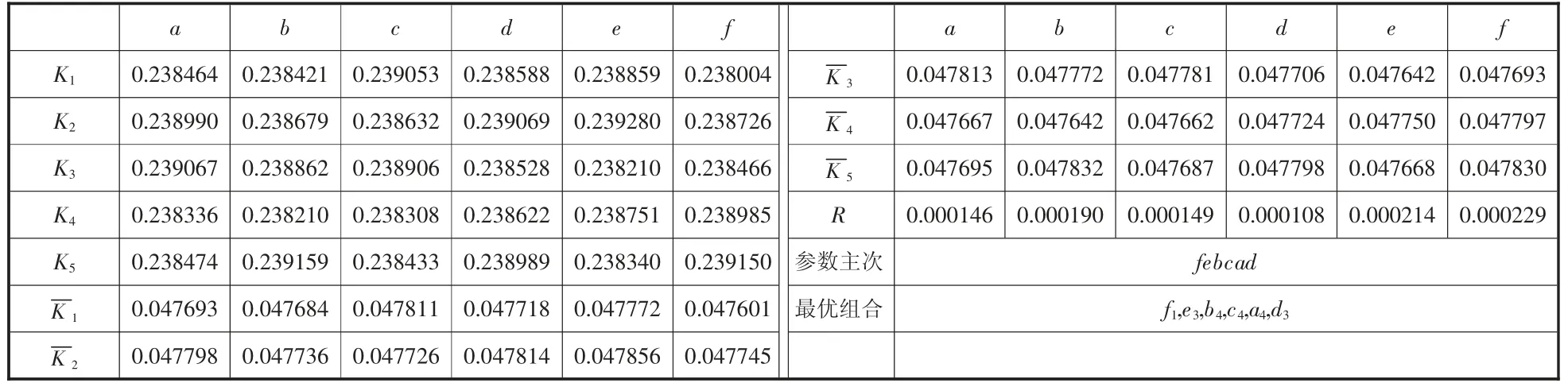
表11 试验数据极差分析结果

依据最优组合，设置仿真平台参数，进行仿真，得到0～3 600s 时仿真路网边界入口的仿真流量，与路网各边界入口的实际流量做对比，得到MAPE值，如表12 所示。最优组合参数下路网边界入口的MAPE小于5%，满足精度要求。说明校正后的仿真结果与实测数据接近，误差在可接受范围之内，由此可见，所采用的最优参数组合是有效的，能真实再现路网的交通运行状况。

3 结束语

针对通过搭建真实车联网环境来验证各种实验研究的难度较大且成本较高问题，本文以广州实际路网为实验区域，利用Vissim 交通仿真软件，给出了车联网仿真实验平台的具体搭建过程，并给出了基于正交试验法的模型参数具体校正过程，校正结果表明所采用的最优参数组合是有效的。但该平台通过读取车辆信息文件，模拟车联网环境，未能实时跟踪车辆状态，要实现真正的车联网环境，需通过Vissim COM 接口进行二次开发，此外，由于正交试验法是在一定范围内穷举了若干套组合方案，不一定是最优方案，因此，后续还需研究自动标定参数的方法。

图7 各参数与的趋势图

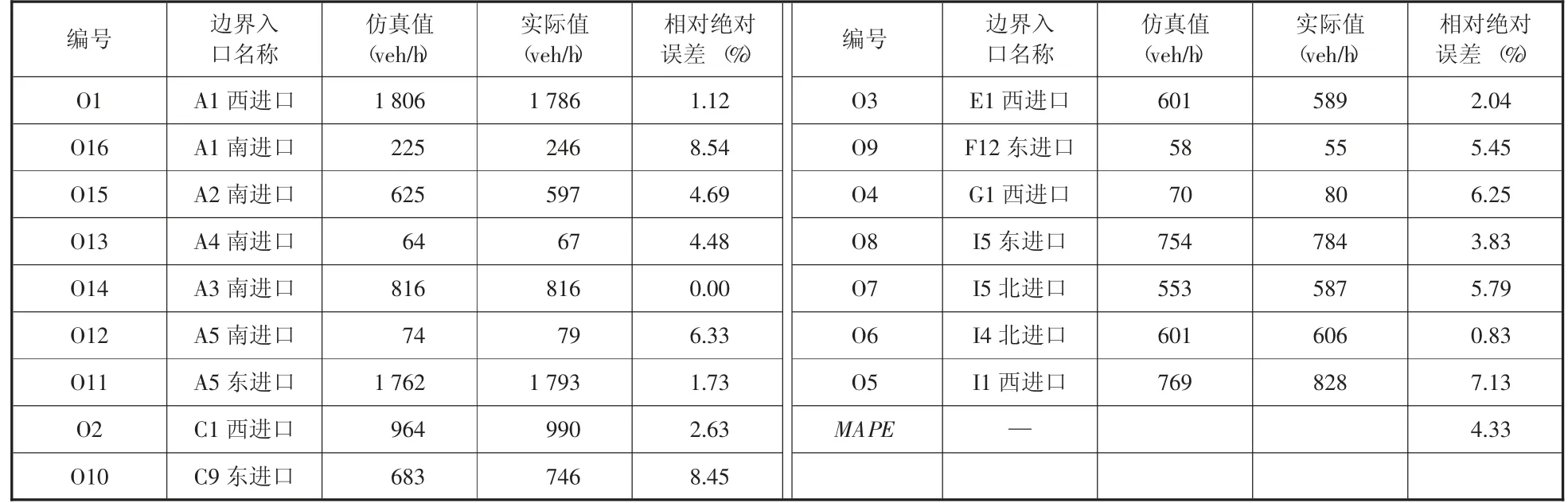
表12 最优组合参数仿真结果分析（0～3 600s）