基于随机函数-谱表示的高阶矩结构动力可靠度分析方法
2020-05-13张龙文卢朝辉
张龙文 卢朝辉
摘要:基于随机函数一谱表示模型,提出了结构响应极值前四阶矩的计算方法,发展了非高斯随机激励下的结构动力可靠度分析的高阶矩方法:(1)修正了随机函数单个基本随机变量的离散点集表达式;(2)根据修正的离散点集生成少量的非高斯加速度时程样本并进行结构时程分析,从而估计得到结构响应极值的前四阶矩(均值、标准差、偏度、峰度);(3)提出了四阶矩可靠指标的完整表达,并应用于计算在非高斯随机激励下的结构动力可靠度。最后,以双自由度系统及八层框架结构的动力可靠度分析为算例,验证了本文方法的精确性与高效性:在样本数量明显减少的情形下,本文方法计算的前四阶矩与Monte Carlo模拟结果相比最大相对误差为5.54%,且动力可靠度分析结果几乎一致。
关键词:随机函数一谱表示;动力可靠度;非高斯随机激励;前四阶矩;四阶矩法
中图分类号:0324;TU311.3;0213.2文献标志码:A 文章编号:1004-4523(2020)02-0265-11
DOI:10.16385/j.cnki.issn.1004-4523.2020.02.006
引言
在工程结构的动力可靠度分析中,为了简化计算,往往将随机激励视为高斯过程。然而,在实际工程中,随机激励如地震、风荷载以及波浪力等均表現为非高斯特性,在非高斯随机激励下结构的响应即使是线性系统也表现为非高斯特性。此时,利用经典的Poisson模型或Markov模型计算首次穿越概率或动力可靠度将可能产生很大的误差。研究者们开始探究工程中非高斯随机过程的动力可靠度问题,但目前只能针对一些特定的非高斯过程,如wiener过程,且计算较为复杂。一般地,计算基于首次穿越破坏机制的结构动力可靠度可以转换为计算结构响应极值分布的问题。在概率统计分析中,随机变量前四阶矩(均值、标准差、偏度与峰度)具有明确物理意义,能够反映分布特性且相对容易求解。因此,本文试图通过求解结构响应极值的前四阶矩,进而利用高阶矩方法实现非高斯随机激励下结构动力可靠度分析。
非高斯随机激励模型的选择直接影响结构响应分析与响应极值前四阶矩的计算。非高斯随机激励研究已取得了一些进展,例如,sakamoto等基于两点相关函数以及Karhunen-Lofve(K-L)展开,发展了非高斯随机过程合成方法,但由于模型较为复杂,利用其进行结构分析时有一定的计算困难。还有一些为某一具体非高斯分布的随机激励类型提出的方法,使得结构响应统计矩的计算方法只能适用于某一特定情况而不具有一般性。例如,Grigoriu等基于Shanon的采样定理和MonteCarlo模拟(MCS)发展的计算矩的方法,在结构分析中,仅考虑了平稳带限非高斯过程激励;waisman等利用摄动法对Duffing振子进行了分析,考虑的非高斯激励类型为滤过Poisson过程多项式。尽管在非高斯随机激励下,MCS方法可用于计算结构响应极值的前四阶矩,然而,MCS方法计算耗时,当结构系统较复杂且失效概率较小时,计算效率更低。为了提高计算效率,陈建兵等提出了随机过程的随机谐和函数表达式,减少了随机变量的数量。同时,陈建兵等进一步对谱表示方法的随机过程中的频率选点进行了优化。近年来,Liu等提出了随机函数一谱表示方法,仅用1到2个基本随机变量较为简单地表示非高斯随机过程,该方法进一步减少了随机过程的随机变量个数,且计算效率明显提高。同时,该方法为进行随机激励下的高效结构反应分析以及统计矩的计算提供了一条新的途径。然而,该方法所产生的加速度时程的均值可能不为0,原因在于离散点集在0点及其附近对应的正交随机变量均值取值会发生突变。
鉴于此,本文基于随机函数一谱表示模型,采用单个基本随机变量,修正了离散点集的表达式,进而提出了结构响应极值前四阶矩的计算方法并结合四阶矩标准化函数应用于非高斯随机激励下的动力可靠度分析。本文以胡聿贤一周锡元功率谱为例,基于修正的离散点集表达式得到了一系列有限少量输入样本时程,并说明了获取结构响应极值前四阶矩的过程;最后,结合双自由度系统及八层框架结构算例说明了本文方法在结构响应极值前四阶矩的计算及动力可靠度分析中的高效性与精确性。
1基于随机函数-谱表示模型的结构响应极值前四阶矩计算
1.1随机函数-谱表示模型
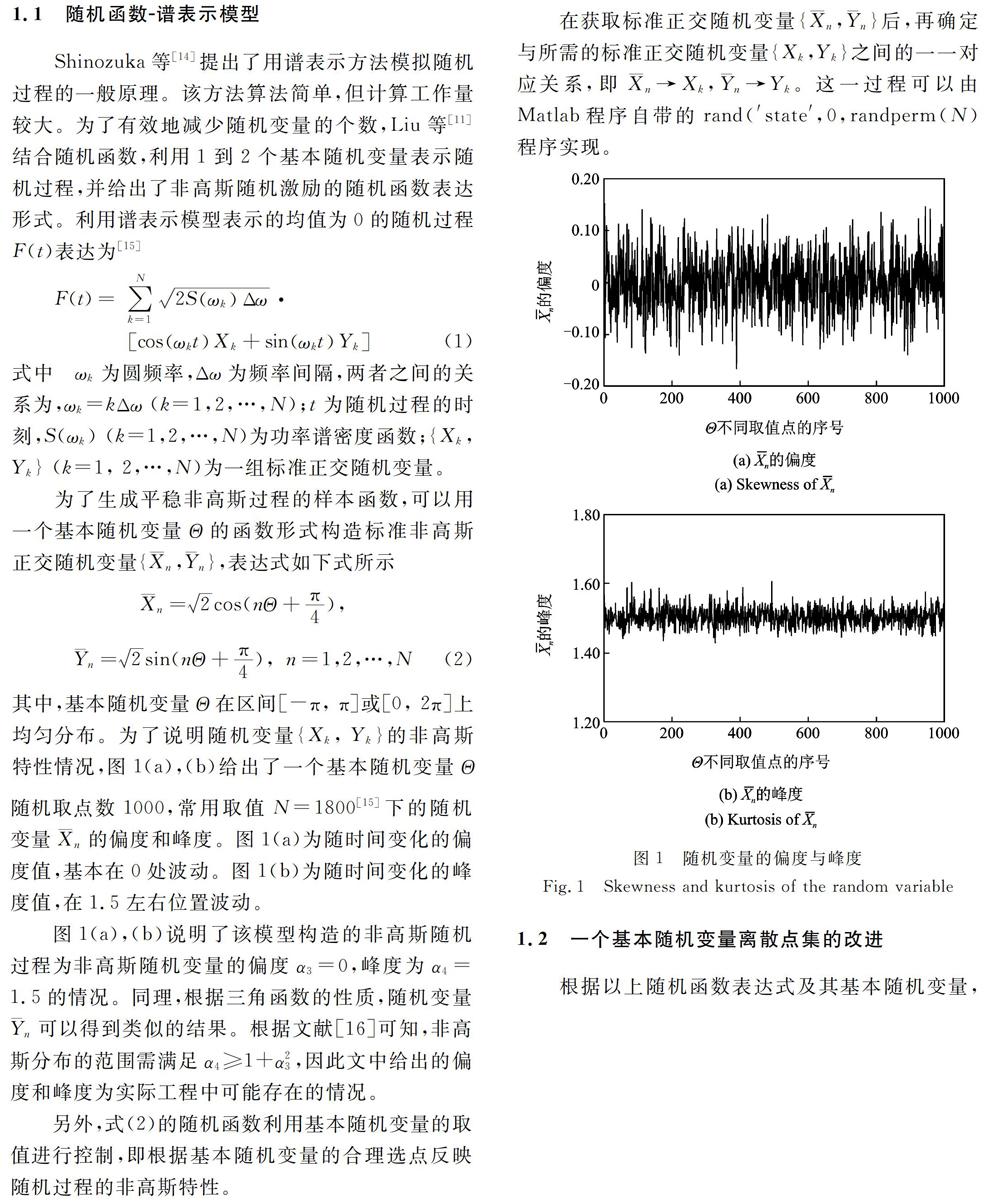
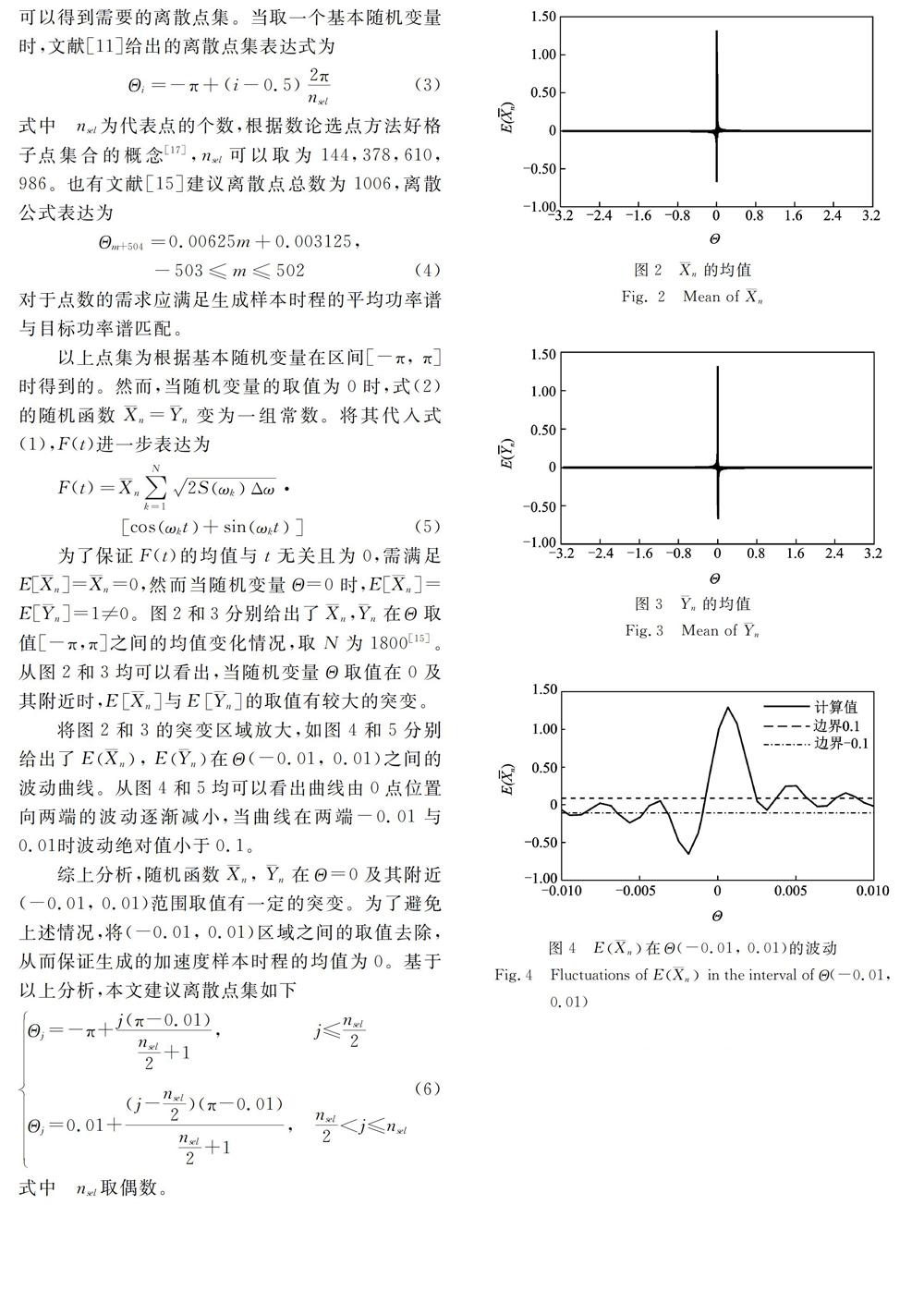
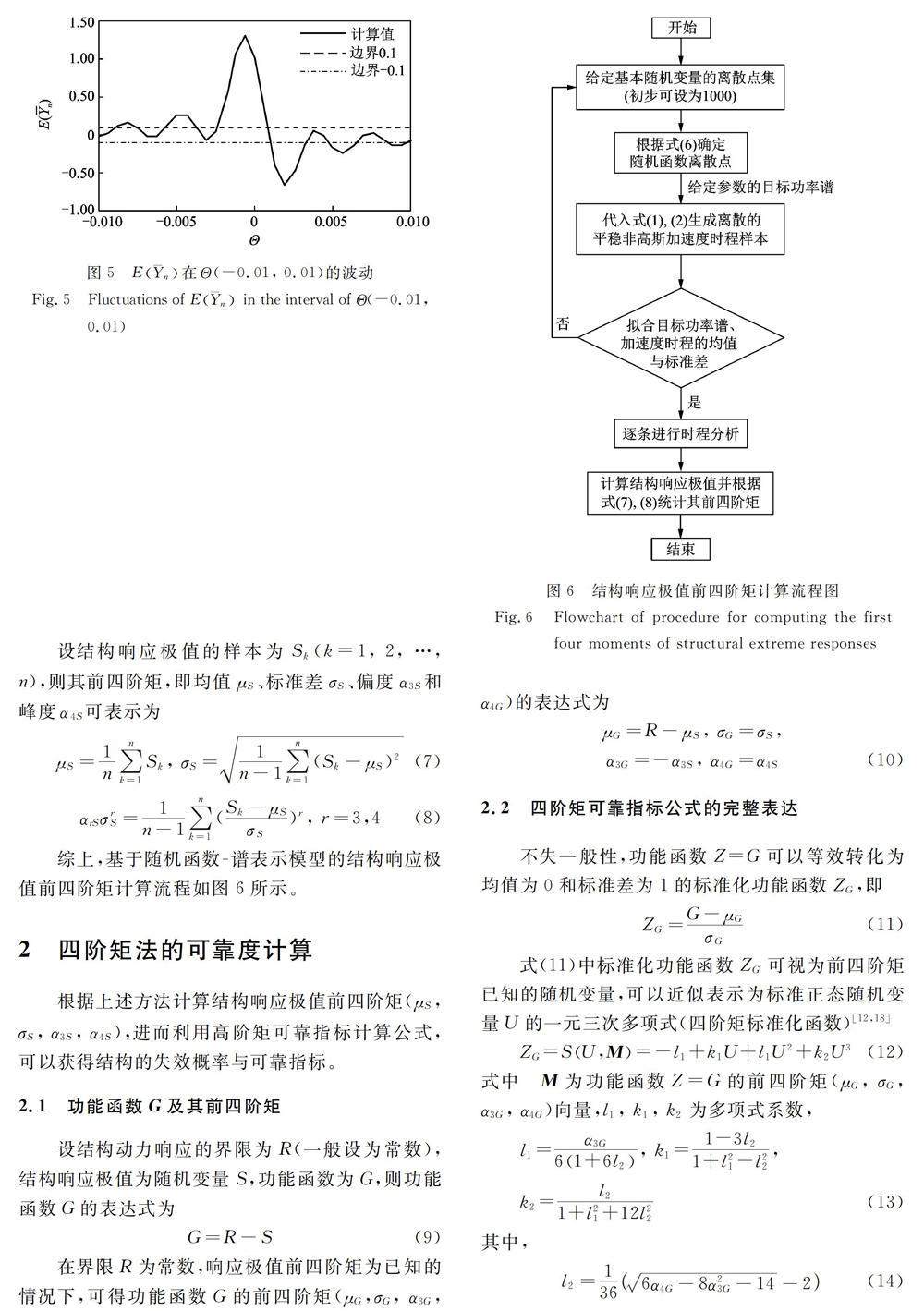
Shinozuka等提出了用谱表示方法模拟随机过程的一般原理。该方法算法简单,但计算工作量较大。为了有效地减少随机变量的个数,Liu等结合随机函数,利用1到2个基本随机变量表示随机过程,并给出了非高斯随机激励的随机函数表达形式。利用谱表示模型表示的均值为0的随机过程F(t)表达为
1.3结构响应极值前四阶矩
当给定目标功率谱密度函数后,根据式(1),(2),(6)可以获得一系列的均值为0的加速度时程样本。将样本时程输入结构进行时程分析,可以获得所需的结构响应极值前四阶矩,具体步骤如下:
(1)根据式(6)初步确定基本正交随机变量的代表点集,初步可设为1000。
(2)模拟非高斯加速度时程样本。根据步骤(1)得到的代表点集代人式(2),可以得到一系列的{Xn,Yn),再根据Matlab自带程序得到{Xk,Yk),进一步根据式(1)可得对应的非高斯加速度时程样本。当计算所得的非高斯加速度时程样本的功率谱均值、加速度时程均值及标准差与其目标值拟合良好,则说明确定的点数满足要求。若不能拟合良好,则回到步骤1重新确定点数。在本文中设置计算的均值与其目标值的允许误差为0.5;标准差、功率谱与其目标值的允许相对误差为5%。
(3)根据生成的非高斯加速度时程样本对结构进行时程分析,进而得到各非高斯加速度时程下的结构响应极值样本。最后,对响应极值样本进行统计分析,得到结构响应极值的前四阶矩。
利用本文建议的离散点集公式(6)以及式(1)计算得到1000条非高斯加速度时程样本,如图7所示。图8给出了1000条加速度时程计算得到的平均功率谱与其目标功率谱的拟合曲线,两者功率谱的相对误差控制在5%以内。从图8可以看出,功率谱密度函数拟合情况良好,曲线基本重合。图9为根据式(1)计算得到的一条典型的加速度时程样本,样本的持续时问为20s。图10(a),(b)分别给出了1000条加速度时程样本计算的总体均值、总体标准差与其相应的目标值的拟合曲线,其中均值与其目标值的最大允许误差为0.5,标准差与其目标值的允许相对误差为5%,从图10(a),(b)分别可以看出,均值、标准差与其目标值均拟合良好。
为了说明生成的非高斯加速度过程的非高斯特性,图11给出了非高斯加速度过程样本分布与正态分布的概率密度函数PDF,从图中可以看出,非高斯随机过程样本分布与正态分布有一定的差异,差异的原因在于非高斯随机过程样本的高阶矩如偏度与峰度(三阶矩与四阶矩)对分布的概率密度函数有一定的影响。
3.2双自由度体系
考虑一个双自由度体系(如图12所示),在上述非高斯随机激励下的动力可靠度问题。设体系的质量m1=1000kg,m2=2000kg,K1=K2=K3=10。N/m分别为三段连接弹簧的刚度。
为了与本文方法计算结果对比,图13给出了m1在不同模拟次数下的位移响应极值前四阶矩(均值、标准差、偏度和峰度)的变化曲线图。从图中可以看出当模拟次数达到10000次时基本稳定,因此本文选取10000个样本下的MCS計算值为标准值如表1所示。根据第1节所述的随机激励,计算得到m1的位移响应极值,如图14给出了m1位移响应极值的概率密度函数(PDF),同时给出了正态分布下的PDF。从图14可以看出,由于响应极值的非高斯特性,m1响应极值的概率分布与正态分布有很大的差异。接着,根据本文方法计算m1的响应极值前四阶矩,结果如表1所示。同理,表1也给出了利用本文方法与MCS计算的m2的位移响应极值前四阶矩。从表1可以看出,利用1000个点计算得到的前四阶矩与10000个样本下的MCS结果基本吻合,最大相对误差为2.45%,最小相对误差为0.08%。
接着,根据计算的前四阶矩以及第2节所述方法计算该体系m1,m2在不同界限下的失效概率及可靠指标,分别如图15及16所示。同时,图15及16均给出了10000个样本下MCS方法的计算结果。图15给出了质点m1从极值位移均值附近开始增大的界限值即R=15至30mm下的失效概率与可靠指标。图16给出了质点m2从位移极值均值附近开始增大的界限值即R=20至40mm下的失效概率与可靠指标。从图15和16均可以看出,本文方法计算结果与MCS结果拟合良好,曲线基本重合。由于本文方法只需1000个点就能得到MCS方法10000个样本下的结果,说明了本文方法的高效性与精确性。
3.38层框架结构
从表2可以看出,本文方法计算得到结果基本与MCS结果吻合:其中,本文方法计算的均值与标准差的大部分数据与MCS计算结果相同(保留4位有效数字),三阶矩a3s的最大相对误差为4.47%,四阶矩a4s的最大相对误差为5.54%。
根据表2各层的前四阶矩,图18给出了各层层问位移角极值的均值曲线,从图中可以看出第二层的层问位移角极值的均值最大。为了计算该框架结构体系的失效概率,本例以层问位移角极值均值最大的第二层可靠度作为该框架结构的整体可靠度。因此,利用第二层层问位移角极值的前四阶矩进行结构的动力可靠度分析。根据表2第2层的前四阶矩,利用本文方法分别计算界限R=0.020%,0.021%,0.022%,0.023%,0.024%,0.025%的结构失效概率与可靠指标。
如图19所示,给出了本文方法计算的在不同界限下的失效概率与可靠指标。同时,图19也给出了10000个样本下MCS的计算结果。从图19(a)的失效概率曲线与图19(b)的可靠指标曲线均可以看出,本文方法计算结果与MCS计算得到的曲线基本重合,进一步说明了本文方法的高效性与精确性。
4结论
(1)改进了随机函数中一个基本随机变量的离散点集表达式,保证了生成的加速度时程样本均值为0。通过1000个离散点集产生的加速度时程样本集合能够很好地拟合目标功率谱、目标均值与目标标准差。
(2)提出了非高斯随机激励下结构响应极值前四阶矩的计算方法与四阶矩可靠指标的完整显式表达,在此基础上发展了基于高阶矩法的动力可靠度分析方法。
(3)通过对双自由度体系以及八层框架结构分析,说明了本文方法在非高斯随机激励下计算结构动力可靠度的运用。计算结果表明本文1000个点的计算结果与MCS结果吻合,说明了本文方法的高效性与精确性。
(4)在实际工程中,由于地震、脉动风等都具有一定的非平稳性,因此,在后续的研究中,考虑非平稳非高斯随机激励下的结构动力可靠度是需要进一步深入的问题。
