大数据背景下学生消费水平分析模型的建立

范媛 蔡敏

摘要：该研究以中国石油大学（北京）的校园卡系统消费数据为数据源，建立数据仓库，通过数据清洗和数据挖掘得到学生在食堂的消费数据。通过使用聚类算法对学生消费数据进行分类，进而将学生的消费水平分为四类。以马氏距离作为判别距离建立学生消费水平判别分析模型，利用该模型判断学生的消费水平，通过对学生消费水平的分析研究，可以在学校有关部门进行决策时提供有效依据。

关键词：校园卡系统;大数据;聚类算法;判别分析;消费模型

中图分类号：TP311 文献标识码：A

文章编号：1009-3044（2020）08-0005-03

开放科学（资源服务）标识码（OSID）：

校园卡系统具有身份识别和电子钱包等功能，实现了校内统一身份认证和消费统一管理，校园卡使用数据完全记录了使用者在校内的消费情况和行为轨迹，通过对校园卡数据的挖掘分析，对高校数据决策具有十分重要的意义。目前各大高校均展开了对校园卡大数据的挖掘分析，来为有关部门进行学生管理提供真实、有效的数据支撑[1]。校园卡系统内积累的大量消费数据，对其进行挖掘分析可以掌握学生在校消费的偏好和规律，将对学校优化资源配置、数据化决策等提供重要参考。该研究通过建立学生消费水平判别模型，将学生消费水平分为4类，可为贫困生认定提供判定依据[2]，为深入研究学生消费水平提供有效方法。

1 数据仓库建立

该研究用于进行分析的数据是以中国石油大学（北京）2018级本科生消費数据作为数据源，抽取学生就餐率较高的2018年11月、12月和2019年3月份的消费数据共计32万多条进行分析，由于数据量庞大，为了不增加数据库的压力并且满足数据分析和数据挖掘的需求，数据分析过程不与校园卡系统数据库直接建立关系，而是通过soL数据库建立数据仓库[3]进行分析。

1.1 数据源确认

通过采集校园卡系统内学生消费数据作为数据源进行分析，进而可以掌握学生的消费习惯，消费水平等情况，在不增加校园卡系统数据库压力的前提下将学生的消费流水数据提取到指定数据库中，把数据处理成可用的数据。

1.2数据预处理

校园卡消费数据中包含了大量信息，包括时间、地点、商户、消费金额、人账信息等，根据分析需求对消费数据进行清洗，去除包含噪声的无意义数据以及无用的字段，并对清洗后的数据进行数据转换[4]。

1.3 建立数据仓库概念模型

对校园卡系统内学生消费数据进行分析，一般按照消费次数、消费金额、消费时间、消费地点等字段进行分析，建立的数据仓库所需要的数据包括：学生基本信息、消费信息、校园卡系统终端数据，数据挖掘的关键性能指标是学生校园卡消费流水信息。

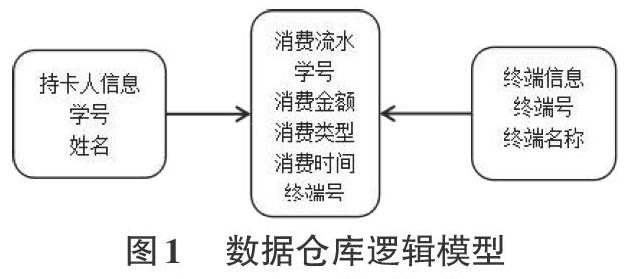
1.4 建立逻辑模型

逻辑模型的建立主要用于划分数据维度，对学生基本信息、消费流水、消费终端信息等数据进行分类储存、数据简化、同属类别归并。逻辑模型如图1所示。

1.5 建立物理模型

建立物理模型的目的是构建合理的数据库物理结构，通过合理规划数据库的结构、字段、索引、存储等，来实现模型的建立，从而可以清楚地对学生消费数据进行分析。物理模型如表1所示。

2 数据挖掘

在此次学生消费水平分析中，通过对校园卡消费数据进行数据清洗，抽取出分析所需的字段，再通过数据清洗与转换将抽取出的数据进行处理转换为用于数据挖掘的形式[5]。

数据来源于校园卡系统学生消费数据，将数据中可压缩的、可合并的、含噪声的以及可删除的字段进行数据清洗与数据合并，通过约减相关性保持数据原貌，达到尽可能地减少数据量的目标[6j。在不同的应用场景中，按照不同的关键词进行数据合并，在分析学生的消费水平时，选取学号作为关键词进行数据合并。该研究利用MATLAB对消费数据进行处理，得到了学生在3个月的月消费数据。

3 建立学生消费水平模型

3.1 聚类分析

K-means聚类算法是聚类分析中应用最广泛的聚类算法之一，是一种发现给定数据集k个簇的算法[7-8]。

针对学生消费水平的研究中，取学生平均单笔消费额和总消费次数为评价指标如表2所示。由于这两项指标的量纲和数量级不同，为了便于决策评价，故对原始数据进行极差规格化变换处理。

极差规格化变换是从数据矩阵的每一个变量中找出其最大值和最小值，这两者之差称为极差，然后从每个变量的每个原始数据中减去该变量中的最小值，再除以极差，就得到规格化数据。即：

经过规格化变换后，数据矩阵中的每列即每个变量的最大数值为1，最小值为0，其余数值取值均在0-1之间;并且变换后的数据都不再具有量纲。根据上述公式变换后的评价指标数据如表3所示。

通过聚类算法对极差规格化变换后评价指标进行聚类。确实聚类数目为4，得到各类的中心结果以及各类的类内元素与中心的距离和（如表4所示）学生消费水平的分类结果（如表5所示），聚类结果示意图如图2所示。

通过聚类分析结果可得类别A的学生消费水平特点为：消费次数低于均值，但平均消费金额高于均值;B类的学生消费水平特点为：消费次数处于均值水平，平均消费金额低于均值;C类的学生消费水平特点为：消费次数高于均值，平均消费金额低于均值水平;D类的学生消费水平特点为：消费次数高于均值，平均消费金额高于均值水平。由此可推断出学生家庭经济状况，A类消费水平的学生很少在食堂吃饭，并且单笔消费金额高，可认定为家庭条件良好，B类消费水平的学生经常在食堂吃饭，但单笔消费金额较低，认定为家庭条件一般贫困，C类消费水平的学生基本在食堂消费，单笔消费金额低于平均水平，认定为家庭条件贫困，D类消费水平的学生在食堂消费次数高于均值，且单笔消费金额较高，认定为家庭条件较好。

3.2 判别分析模型

根据距离判别分析原理，选用马氏距离作为判别距离[9]，针对学生在校食堂消费水平建立了学生消费水平距离判别的分析模型，利用该模型判别学生的消费水平。

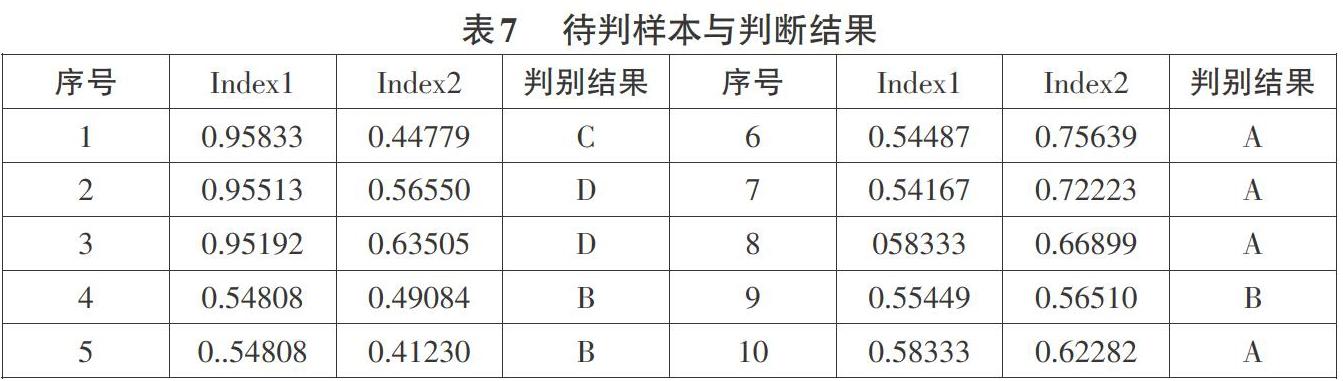
式（8）即是学生消费水平判别分析模型，通过该模型可对学生消费情况进行判别。将学生消费水平数据代入式（8）中，即可判断其所属类别。将训练样本数据回代判断结果如表6中所示。选取10组学生消费数据作为待判样本，以此模型对待判样本进行判别，得到结果如表7所示。

（5）判别准则评价

通过3.2.4中训练样本回代，样本总量为80组，正确判别数为78，误判数为2，计算得到误判概率为2.5%，可见此模型合理，达到了对学生消费水平进行有效分类的效果。

4 结论

该研究通过构建数据仓库，得到有效的学生校园卡消费数据。通过聚类算法将学生的消费水平分为四类，可根据消费水平判定学生家庭经济情况.为贫困生资助提供数据支持;利用以马氏距离作为判别距离的判别算法建立学生学费水平判别模型，用以判别学生消费水平的分类是否有效。

参考文献：

[1]张艳分，卢小清，刘禹等.基于大数据平台的大学生校园行为探析[J].中国教育信息化，2019（1）：39-42，46.

[2]张林.基于差分隐私保护技术的高校贫困生认定系统设计[J].计算机技术与自动化，2017（3）：151-156.

[3]田雨露.基于校园一卡通系统的决策支持和数据分析研究[D].北京化工大学，2018.

[4]万晓燕.基于聚类划分的大数据处理方法研究[J].智库时代，2019（39）：280，283.

[5] Nguyen T V，Zhou L，Loong A Y，et al-Predicting customerdemand for remanufactured products：A data-mining approach[J]. European Journal of Operational Research， 2019（8）： InPress.

[6]潘晓英，赵倩，赵普.时空属性关系标签的频繁轨迹模式挖掘[J].计算机工程与应用，2019，55（10）：83-89.

[7]陆近，郭跃近.一种含噪声处理的K-means聚类算法[J].计算机应用于软件，2015，32（10）：265-268.

[8]邹晨紅，袁满.模糊综合评判的系统聚类算法研究[J].吉林大学学报：信息科学版，2018，36（5）：441-448

[9]张华平.常用判别分析方法的综合比较[J].统计与决策，2015（22）：77-78.

[10] Wang B X，Zou H.A Multicategory Kernel Distance Weight-ed Discrimination Method for Multiclass Classification[J].Technometrics，2019，61（3）.

[11] LIN T，Chen G，Ouyang W L.et al-Hyper-spherical dis-tance discrimination： A novel data description method foraero-engme rolling bearing fault detection[J].Mechanical Sys-tems and Signal Processing，2018，109（9）.

[12]相诗尧，邢会敏，徐东晶.空间点所属空间体的距离判别法分析[J].测绘科学，2016，41（6）：40-43，112.

【通联编辑：王力】

作者简介：范媛（1980-），女，河北南和人，硕士，工程师，主要从事高校一卡通和信息化建设;蔡敏（1995-），女，甘肃庆阳人，硕士在读，化工过程机械专业。