SPC 试验设计在改善铁道车辆缓解速度 过程中的探索

张兴川 刘元森 杨德胜

（成都铁路局集团公司重庆西车辆段， 重庆）

0 引言

随着近几年我国经济的发展和社会主要矛盾的转变，总公司对铁道车辆的运行品质和运行效率也提出了更进一步的要求，图1 为我段

图1 车辆缓解时间均值控制图

检修车辆缓解时间的控制图，从图上可以看出我段检修车辆的缓解性能较低，还有很大的改善空间，并且车辆缓解时间越短一方面能说明车辆的整体性和车辆的运行品质越佳；一方面能缩短整列车辆在各作业场的停留时间和运行过程中制动缓解时间，减少整列车辆整趟运行的时长，提升运输效率。SPC 中的DOE 试验设计是数理统计为根基，将试验科学合理化得一项技术，具有减少成本、缩短产品试验周期、降低产品质量波动的特点[2]。本项目主要通过DOE 试验找出了影响铁道车辆缓解时间的显著因素，为提升铁道车辆整体缓解性能提供了可靠的理论依据。

2 SPC 试验设计

DOE 试验设计是根据最好工艺结果的要求，设计一组试验次数较少的工艺试验，通过对设计试验的结果数据进行统计分析，建立能反应生产工艺结果和工艺输入条件间关系的统计模型，从而确定能实现期望工艺结果的最优工艺条件，DOE试验设计基本可分为DOE 的问题描述和分析、输入变量因子和水平的确定、试验方案的确定和执行、试验数据分析、建立工艺模型优化生产工艺的条件等步骤，其凭借可以减小试验规模、缩短试验周期、降低试验成本、结论科学等优势，在增加工艺生产水平、提升生产过程的成品率、改善工艺性能、工艺开发等诸多方面起着非常重要的作用[2]。

3 车辆缓解时间的DOE 优化设计

3.1 车辆缓解时间影响因素分析

3.1.1、因子查找

本试验将车辆在缓解感度试验时的缓解时间作为车辆的缓解时间进行数据采集，使用鱼骨图从人机料法环等方面分析了影响输出响应的因子，详细情况如图2所示，共找出了16 个影响车辆缓解时间的因子，但所找出的因子并不全都是影响车辆缓解时间的重要因子，因此还需通过因果矩阵进一步的筛选出关键因子。

图2 影响车辆缓解时间因子分析图

3.1.2、因果矩阵筛选

结合车辆检修实际情况和相关的理论依据，对图2 筛选出的因子进行打分筛选， 依据轻微影响（1 分）、一般影响（3 分）、重要影响（9 分）的准则，对上述的因子进行评价，详情如表1 所示。

表格1 车辆缓解时间的因果矩阵筛选评价表

通过上述的评分，可看出传感阀性能、限压阀性能、制动缸尺寸是影响车辆缓解时间的重要因子，而在车辆检修过程中，车辆的制动缸尺寸不能改变，因此可确定传感阀、限压阀的性能是影响车辆缓解时间的关键性因素。

3.2 改善车辆缓解时间的方案

传感阀、限压阀的性能是本试验的因子，现车单车缓解感度试验时的缓解时间是响应，而传感阀、限压阀的性能不同其在试验台上的缓解时间也不同，因此本试验将传感阀、限压阀在试验台上空车位的缓解时间作为因子的水平，因子的高水平和低水平分别取试验台上空车位的最小和最大的缓解时间值。而我段检修的限压阀在试验台上空车位的缓解时间都在2s-4s 之间，限压阀的缓解时间只有2s、3s、4s 三种情况，并且缓解时间都比较靠前，说明限压阀的缓解性能比较优越，因此本试验可以忽略限压阀对车辆缓解时间的影响，只验证传感阀的缓解性能是否对车辆的缓解时间具有显著性的影响，具体的试验设计方案和试验数据如表2、3 所示。

表格2 试验设计方案

表格3 试验采集数据

39.22 33.43 43.00 38.00 37.31 35.87 41.50 38.34 35.98 40.76 38.00 40.90 38.23 39.98 40.37 41.22 35.65 40.22 41.85 35.87 40.96 38.55 36.85 33.84 41.50 36.09 40.06 41.41 38.98 40.95 41.59 34.88 40.65 36.06 36.47 41.11 37.35 36.29 40.82 39.20 35.20 41.02 41.98 36.11 41.23

3.3 试验数据分析

3.3.1 试验数据处理

1、试验数据箱线图分析

对采集到的编组1、2、3 的试验数据使用箱线图检测是否存在异常值，结果如图3 所示，从图中可看出编组3 采集到的数据存在异常值，将异常值剔除，编组3 删除异常值后的箱线图如图4 所示，整组数据无异常，可进行一下步的数据处理。

2、数据的正态性检验

在对数据进行最终方差分析判断因子是否对响应有显著性影响前，需验证实验数据三个条件：①在各水平下的试验数据需服从正态分布②在不同水平下的方差偏差一致性③采集到的试验数据相互独立。而本试验在相同的条件下进行且试验的次序是随机化的，因此方

差一致性和数据的相互独立的条件能得到满足，只需对数据进行正态

图3 编组1、2、3 的箱线图

图4 编组3 删除异常数据后的箱线图

性校验即可。图5 为编组1、2、3 的概率图，从图中可看出3 组试验条件下采集到的数据都符合正态分布（p 值＞0.05），方差分析的三个基本假设得到满足，接下来可以通过方差分析进行影响因子的显著性判断。

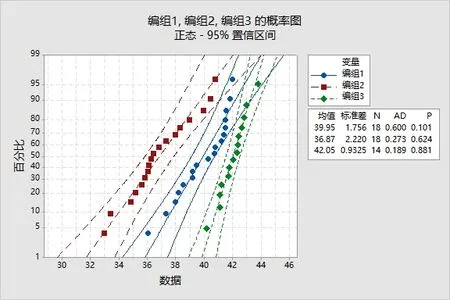
图5 编组1、2、3 的概率图

方差分析的三个基本假设得到满足可以进行通过方差分析进行影响因子的显著性判断。

3.3.2 方差分析

在试验过程中存在系统误差和随机误差等两类波动，而方差分析就是将上述两种波动的影响进行区分[2]。本试验为单因子试验，需采用以下方差分析公式进行计算统计量F 来进行原假设检验，以此判断缓解阀性能对车辆缓解时间是否具有显著性影响。

其中：m-因子选取的水平个数 n-每个水平重复的次数

Q-各组数据之和的平方除以本组数据个数之后在求和

通过上述公式计算得到的各个值如表4 所示。

表格4 传感阀的方差分析表

3.4、方差分析结论

根据上述公式可得统计量FA=34.78＞F（2，47，0.05）=3.195，说明传感阀性能对车辆制动缓解时间具有显著影响。

3.5 结论和下一步建议

1、传感阀性能对车辆缓解时间具有显著性影响，因此可以通过改善传感阀的性能来提高铁道车辆的缓解性能。

2、探讨传感阀缓解性能和车辆缓解性能的函数相关性。

3、在实际生产过程中验证传感阀缓解性能对车辆缓解性能的显著性影响。