非收放式减摇鳍鳍轴校核算法研究

蒋衡捷，曹长水，邓启亮，司黎明

（上海衡拓船舶设备有限公司，上海 200031）

0 引言

依靠装在船舶两舷水下的可动鳍翼上产生的流体动力效应，实施减摇的装置成为减摇鳍装置。主要可分为收放式与非收放式减摇鳍。顾名思义，非收放式减摇鳍即，鳍无法收进船体。

当船在海洋波浪扰动力矩的作用下而产生横摇运动时，置于船两舷舭部水中的鳍跟随船舶横摇而来的转鳍信号转动至指定的角度值，与水流形成攻角。随着船舶航速的提升，由于流体动力学，鳍上会产生升力、阻力和倾覆力矩。倾覆力矩由油缸产生的力矩相抵消，而升力会对船的重心，也就是船的摇摆中心会形成力矩。只要将两舷的鳍上升力控制成大小相等、方向相反，与海浪引起的扰动力矩相抵消便可达到相应的减摇效果。

鳍上所产生的升力、阻力、倾覆力矩都是通过鳍轴传递到舱内的执行机构再传递到船体上，因此鳍轴作为非收放式减摇鳍设备传力链非常重要的一环，对于每一个型号的减摇鳍装置都需要进行相应的校核计算，本文将对新老2种算法进行相应的研究，并以某型减摇鳍参数为例比较 2种算法的优劣。

1 鳍轴建模及受力分析

图1为右鳍轴，从鳍梢端看，鳍顺时针转动时，鳍轴的受力情况。

G为鳍和鳍轴组的总重。

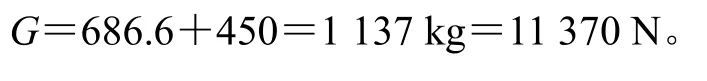
图1 鳍轴受力分析简图（单位：mm）

减摇鳍安装在舭部与水平呈β＝69°，A点为大轴承，B点为小轴承，E处为设备重心，D为流体升阻力作用重心。以某型号减摇鳍数据作为算例，见表1。

表1 流体输入参数表

鳍和鳍轴组总重量G作用与鳍的轴向分量Gx与径向分量Gy为

延鳍轴方向向外为x正方向，垂直于x方向为y方向。

有平衡方程

先计算由升力引起的支反力，由上述平衡方程可得：

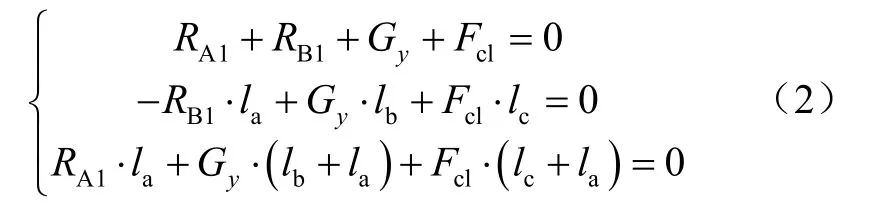
式中：RA1为大轴承处升力引起的支反力，N；RB1为小轴承处升力引起的支反力，N；Gy为鳍轴与鳍总重沿y方向的分力，N；Fcl为鳍所受到的升力，N；la为小轴承到大轴承处的距离，mm；lb为大轴承至鳍轴与鳍重心处的距离，mm；lc为大轴承中心至鳍中心的距离，mm。

其中，已知量为

求解可得：

由阻力引起的支反力为

式中：Fd为鳍所受到的阻力，N。

对式（4）求解后可得式（5）

2 强度理论

强度理论作为推测强度失效原因的假说，是基于一些假设前提的，因此在使用这些强度理论时，应该根据具体的情况、条件选择不同的强度理论。以下简单介绍4种工程上最为常用的强度理论。

最大拉应力理论（第一强度理论）：该理论认为无论什么应力状态，只要最大拉应力达到与材料性质有关的某一极限值，材料就会发生断裂。

最大伸长线应变理论（第二强度理论）：该理论认为最大伸长线应变是引起断裂的主要因素。

前2种强度理论主要应用于铸铁、石料、混凝土等脆性材料，通常以断裂形式失效。而随着20世纪70年代断裂力学的逐渐兴起，也出现了应用于脆性断裂的 K准则，即引入裂纹的概念，通过裂纹是否扩展来判断。

最大切应力理论（第三强度理论）：该理论认为最大切应力是引起屈服的主要因素。而莫尔强度理论在基于实验资料的基础上也可以得出第三强度理论。

畸变能密度理论（第四强度理论）：该理论认为畸变能密度是引起屈服的主要因素，在钢、铜、铝等塑性材料的薄管试验中表明，第四强度理论比第三强度理论更符合试验结果，且在纯剪切的情况下第四强度理论的值会比第三强度理论大15%。而在诸如Ansys、Abaqus等常用有限元分析软件中作为等效应力的Von-Mises应力实际上也是遵循第四强度理论。

3 鳍轴应力校核分析

3.1 旧算法

旧算法是，过去鳍轴的弯扭综合应力校核借鉴舵杆强度校核公式，采用直接计算法校核舵杆强度（CCS《钢制海船入级规范》），但采用第三强度理论作为核算依据。

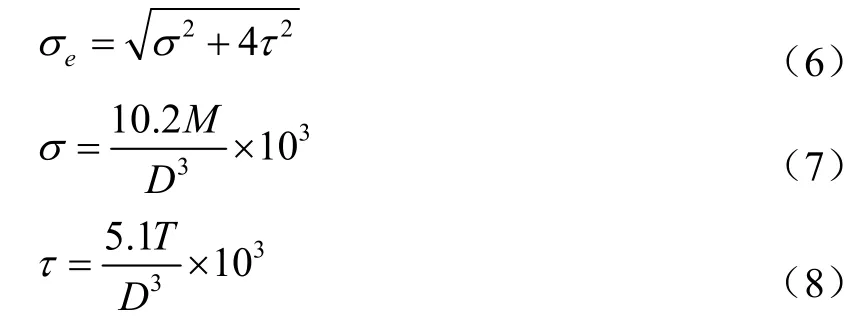
式中：σe为等效应力，N；σ为由弯矩引起的正应力，N；τ为由剪力引起的切应力，N；D为大轴承处直径，D＝200 mm；T为转鳍扭矩，取阻力T＝Mct＝47 835 N·m；M为作用在大轴承处的弯矩，M＝96 756 N·m。

可求解：

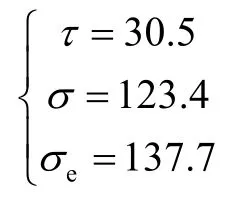
若采用第四强度理论则为：σe＝134.23 MPa。

该算法也常见于机械设计手册，应用于原直杆的弯扭综合应力校核。手册中推荐对于钢材等塑性材料使用第四强度理论，在本算例中，第三强度、四强度理论计算结果相差仅2.3%，可忽略不计。但在该算法中实际上忽略了升阻力引起的支反力，作为剪力对鳍轴零件截面应力所造成的影响，在新算法中将尝试性的弥补该问题。

3.2 新算法

新算法是以鳍轴中心线为x轴，指向舷外为正方向，对于鳍轴上的任一截面可建立如图2坐标系。

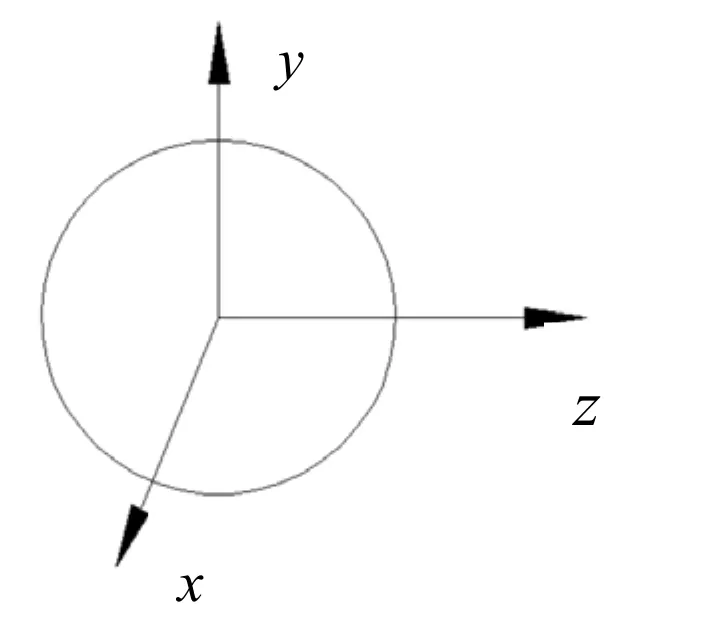
图2 计算截面坐标系

对于截面上的任意一点，有应力：

式中：σx为由升阻力引起的弯矩My、Mz所引起的x方向上的正应力，MPa；τxy为由升力或者升力引起的支反力导致的剪力引起的切应力，MPa；τxz为由阻力或者阻力引起的支反力导致的剪力引起的切应力，MPa；τyz为由转鳍引起的转矩导致的切应力，MPa。

对于任意确定的平面，其计算公式为

由于鳍轴截面都是圆面，为对称图形，则Iyz＝0。

则上式可简化为

式中：Mz为升力与升力引起的支反力引起的弯矩，MPa，其中重力的分力在数量级上，相差了 100倍，可忽略不计。My为阻力与阻力引起的支反力引起的弯矩，MPa。

剪力引起的切应力可通过式（12）进行计算

对于半径为c的截面，如式（13）

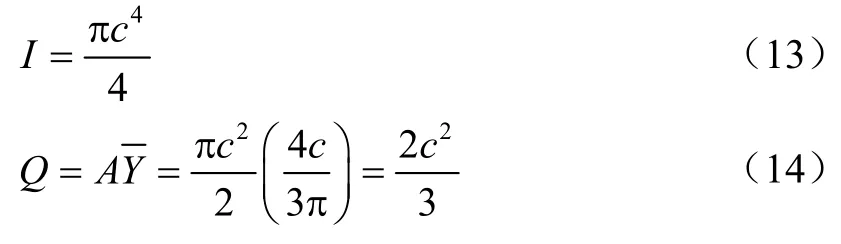
在b＝2c的线上，取得最大切应力为

式中：V为剪力，N；A为圆截面面积，mm2。

同理可得τxzmax

由扭矩引起的切应力可由式（16）求得

其中，对于圆截面

由此，对于任意给定截面，都可求出

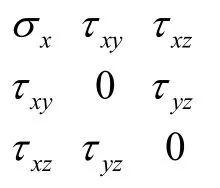
通过求其特征值，可求得其主应力为

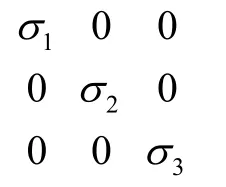
最后根据Von-Mise准则，有

可求得屈服应力yp。

对鳍轴进行分析可知，从小轴承端到锥度起始点，除了2个轴肩以外，截面形状相同，因此仅考虑扭矩与剪力最大处即可。

小轴承到大轴承段：弯矩以小轴承中心点作为x轴0点，可得，在此段上弯矩变化为

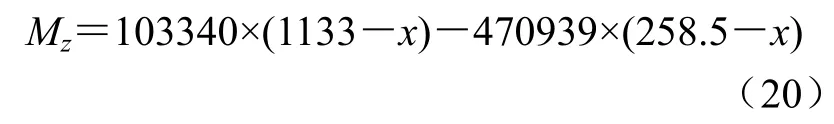
简化后可得

显然，在大轴承截面上弯矩取得最大值。My同理可证。

故在大轴承截面上有

则由弯矩引起的应力为

将z2＋y2＝0.01代入原方程，通过求极值可得在

y＝-0.09处取得最大值，σx＝128.7 MPa。

可得其在该截面上的最大的应力状态为

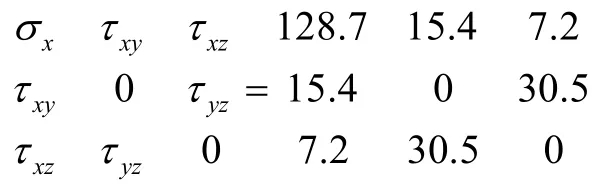
转化到主应力平面即求矩阵的特征向量可得

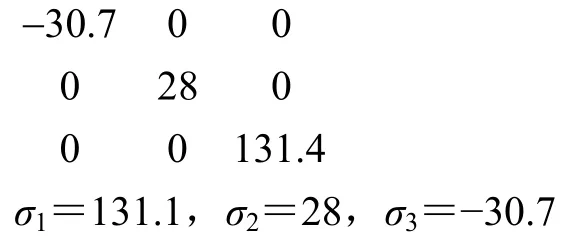
根据VON-MISE准则求得屈服应力为

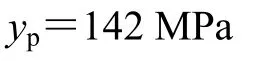
若采用第三强度准则，则

在该受力情况下，第三强度理论的计算结果比第四强度理论大了14%。

4 结论

通过比较发现，在都采用第四强度理论的前提下，新算法考虑了剪力对鳍轴应力造成的影响，其计算值更加接近真实值。新算法值增大约6%。而在第三强度理论下，新算法比旧算法增大了17.7%，比第四强度理论增大了14%，如表2所示。

研究表明，对于较为成熟的产品建议采用旧算法，采用第三或第四强度理论都对结果影响不大；而当应用于新设计的产品时，宜采用第四强度理论下的新算法，更加接近真实值。

表2 新旧算法比较