基于层次蝙蝠算法的应急车辆调度与交通疏散协同决策

段晓红，吴家新，周芷晴

(北方工业大学a.经济管理学院；b.企业管理智能决策研究中心；c.电气与控制工程学院，北京100144)

0 引言

早期应急车辆调度的研究假设救援路径静态已知，以时间最短、成本最低等为目标，从非路径的角度研究调度问题[1].事故和救援环境的动态变化决定了应急车辆调度是一个复杂动态过程.学者将动态问题沿着时间轴划分为多个静态问题，在各静态问题中实时获取参数并更新调度方案.刘亚杰等[2]基于模型预测控制方法建立多周期滚动优化调度模型，在各周期内根据实时信息对调度策略进行调整.一些学者通过构建时间依赖函数描述决策参数的动态变化过程.Ozdamar等[3]将时变资源供给和需求作为关键因素，以总救援延迟时间最短为目标，分阶段求解物资配送策略.Duan等[4]以预测行程车速函数为路段权值，构建应急车辆动态调度与路径选择模型.为求解多目标多变量的调度模型，蚁群算法[5]、粒子群算法[6]等智能优化算法得到广泛应用.

分析文献发现，国内外学者考虑路网的动态特性，基于实时或时变的路况信息规划路径并求解调度策略，引导应急车辆避开拥堵路段.然而，一旦发生交通事故，路网整体通行能力将大幅下降，应急救援时效仍难以保证，此时合理的交通疏散是快速调度应急车辆的有力保障.现有应急交通疏散相关研究集中在应急区域疏散问题，是在一定的时限内，将人员从危险区域转移到安全地点的过程.通常基于网络流或交通分配模型，配合交通控制措施实现疏散效果的优化[7]，鲜有研究应急车辆调度中的交通疏散问题.基于此，本文在应急车辆调度中加入交通疏散因素，针对调度与疏散问题间的层级制约关系，采用双层规划方法构建模型，并设计一种双层蝙蝠算法实现模型的求解.

1 问题描述与建模

1.1 路网模型构建

将路网抽象为一个时变有向网络模型[N,E,T(t)⋅Q,T(l)(t)⋅Q,T(d)(t)⋅Q].I个节点构成集合N={n1,n2,…,nI}，若第i个节点ni与第j个节点nj相连，ni,nj∈N且i≠j，它们之间的连接线构成路段ei,j=(ni,nj)∈E，E为路段集合，路段长度为Li,j，路段交通容量为Q是感兴趣的时间区间，以Δ为间隔将其划分为Φ+1个离散时间段，则Q={[t0,t0+Δ),[t0+Δ,t0+2⋅Δ),…,[t0+t⋅Δ,t0+(t+1) ⋅Δ) ,…,[t0+Φ⋅Δ,Qend] }，其中，t0为初始决策时刻，Qend为时间区间Q的右端点，将t0+t⋅Δ时刻记为t时刻.T(t)、T(l)(t)和T(d)(t)分别为定义在时间区间Q上的行程时间矩阵、交通负荷矩阵和交通需求矩阵.分别表示路段在t(t=0,1,…,Φ)时刻的行程时间、交通负荷和交通需求.H辆应急车辆构成集合S，第h辆应急车辆sh所在节点为，sh∈S.t0时刻发生的D起事故构成集合F，第d起事故fd所在节点为，fd∈F，应急车辆需求为rd，救援时间窗为，事故严重程度为，应急车辆sh到事故fd的最短行程时间为

1.2 应急车辆调度与交通疏散模型构建

应急车辆调度和交通疏散是相互作用的决策过程，表述为一个双层规划问题.上层决策以总救援时间最短为目标选择最优出救车辆；下层决策通过控制车辆行驶路径上的路段流入率，在交通需求和交通容量约束下求取最优路径.

1.2.1 上层应急车辆调度模型构建

式(1)为目标函数，使带事故严重程度加权的应急救援时间最短.式(2)保证派往事故fd的应急车辆数满足其需求rd.式(3)保证应急车辆最晚到达事故fd的时间不超过其救援时效上限.式(4)保证应急车辆sh只能被派往事故fd或为空闲车辆.式(5)保证应急车辆总数为H.式(6)和式(7)为决策变量yh,d和的状态约束.

1.2.2 下层交通疏散模型构建

下层模型包含两个阶段：①以长度为路段权值，构建K最短路径模型，规划出节点到节点的前K条长度最短的路径，将它们作为备选救援路径；②以行程时间最短为目标，对K条备选路径进行交通疏散，并从中选取行程时间最短的一条作为最终救援路径.K最短路径(KSP)模型为

2 基于蝙蝠算法的模型求解

2.1 蝙蝠算法基本原理

蝙蝠算法(Bat Algorithm,BA)是Yang在2010年提出的一种元启发式算法[8]，它模仿蝙蝠回声定位捕食行为，具有结构简单、收敛速度快、自动切换全局和局部寻优等优势.由A只蝙蝠组成种群M，第a只蝙蝠ma的位置xa表示问题的一种可行解，它对应与问题优化目标相关的适应度函数值Pf(xa)，a=1,2,…,A.在适应度函数Pf的引导下，任一蝙蝠个体ma不断更新飞行速度和位置xa以实现种群的全局寻优.随着种群逐渐接近猎物，为当前最优位置添加一个逐渐减小的扰动，由此实现个体的局部寻优.

(1)全局寻优时，φ时刻个体ma的飞行速度和位置xa更新策略为

(2)局部寻优时，从当前种群中选择一个最优位置xold，采用随机游走方案产生新的局部解xnew，即

式中：ε是一个随机数，ε∈[-1,1]；是所有蝙蝠在同一时间段的平均声波响度.

蝙蝠ma的声波响度和脉冲发射速率更新公式为

式中：α为音量衰减系数；γ为脉冲发射速率增加系数；分别为蝙蝠ma的初始声波响度和脉冲发射速率.

(3)基本蝙蝠算法的实现步骤.

Step 1参数初始化.

Step 2对于蝙蝠ma,a=1,2,…,A执行如下操作

Step 2.1根据式(24)～式(26)更新速度和位置xa.

Step 2.2产生随机数，在种群中选择一个最优个体，并根据式(27)在附近产生一个新的局部解

Step 2.3产生随机数，则接受，并根据式(28)和式(29)调整响度和发射速率

Step 3根据适应度从大到小的顺序对种群排序，查找并替换最佳蝙蝠位置x*.

Step 4重复步骤Step 2～Step 3直至最大迭代次数Z，输出全局最优解x*.

2.2 求解双层规划模型的蝙蝠算法

设计一种具有双层架构的蝙蝠算法，上层算法(BA_EVD)求解EVD模型，下层算法集成了两个蝙蝠算法BA_KSP和BA_TE，分别求解KSP模型和TE模型.

(2)下层算法计算最优控制策略ue,k,h,d(t)，uw,i,e,k,h,d(t)和最短行程时间

②BA_TE算法计算路段ek,h,d和wi,e,k,h,d，wi,e,k,h,d∈Wi,e,k,h,d在t∈Q时刻的最佳流入率，获得路径在最佳控制措施下的行程时间，并传递给上层算法.

2.3 求解K条最短路径的蝙蝠算法

为满足路径连通性约束，在基本蝙蝠算法步骤的基础上，重新定义初始编码方案、全局和局部寻优策略.

(1)初始编码方案.

采用整数编码方案进行路径编码，并通过随机邻接搜索策略确保路径的连通性.定义节点ni的邻接节点集合为Ai，当前路径集合为在节点集合N中的补集)中随机选择一个节点ni+1，将当前路径集合更新为一搜索至事故节点，形成蝙蝠的位置编码.

(2)全局寻优策略.

φ时刻蝙蝠ma的位置为路径序列x(a)φ，从中随机选择两个不同的节点位置，构成φ+1时刻ma的速度

2.4 求解交通疏散模型的蝙蝠算法

2.5 求解应急车辆调度模型的蝙蝠算法

应急车辆调度模型的决策变量是0-1变量yh,d，将其转换为整型变量yh，表示应急车辆sh(h=1,2,…,H)的调度方案.sh(sh∈S)可派往事故fd(fd∈F)或为空闲车辆，则yh的可行解集为yh={0,1,2,…,D}.任一蝙蝠的位置编码可表示为

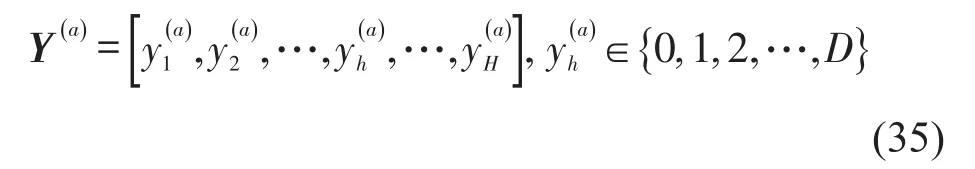
适应度函数与目标函数式(1)，约束条件式(2)和式(3)相关，即

3 算例验证

采用图1所示的路网验证模型和算法的有效性，时间区间Q=[9 : 30,10:30]，时间间隔Δ=60 s，路网内分布有H=10辆应急车辆，具体参数如表1所示.t=9:30时发生D=4起事故，具体参数如表2所示，事故救援时间上限为1 800 s.

图1 路网图Fig.1 Road network

表1 应急车辆参数Table 1 Emergency vehicle parameters

表2 事故参数Table 2 Accident parameters

(1)计算最短路径.

(2)计算疏散方案.

采用BA_TE算法计算任意一条最短路径上各路段及其相连路段的流入率，算法参数设置如表6所示.以路径n13→n24→n25→n26→n27为例，算法寻优过程如图3所示，运行结果如表7和表8所示.

表 3 BA_KSP算法参数设置Table 3 Selection of parameters of BA_KSP algorithm

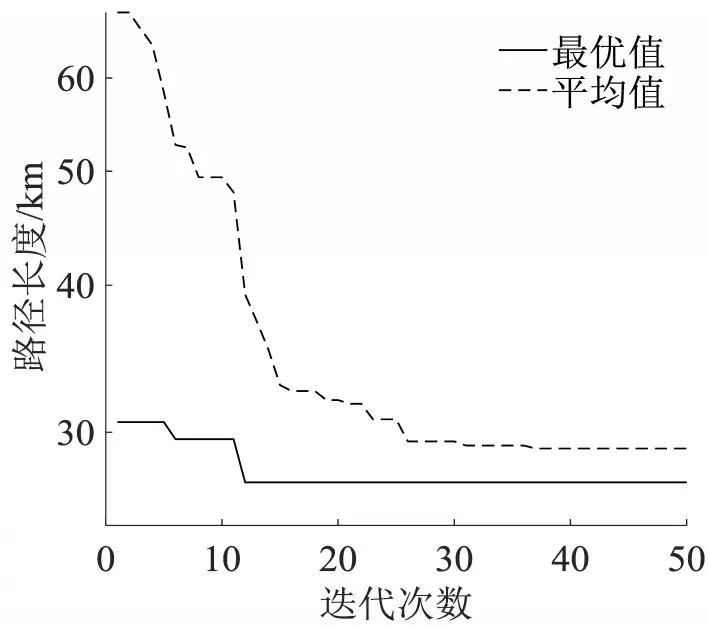
图2 BA_KSP算法寻优过程Fig.2 Evolutionary process of BA_KSP algorithm

表4 的前5条最短路径Table 4 First five shortest paths from

表4 的前5条最短路径Table 4 First five shortest paths from

images/BZ_167_554_468_1971_522.png1 2 3 4 5( n)2 →n8→n9→n10→n11→n12→n13→n14→n27→(n)s f 3( n)s 2→n8→n9→n10→n2→n3→n4→n13→n14→n27→(n)f 3( n)s 2→n8→n7→n1→n2→n3→n4→n13→n14→n27→(n)f 3( n)s 2→n8→n9→n10→n2→n3→n12→n13→n14→n27→(n)f 3 n(s)2 →n8→n7→n1→n2→n3→n12→n13→n14→n27→n(f)3 30.75 31.75 32.05 32.75 33.05

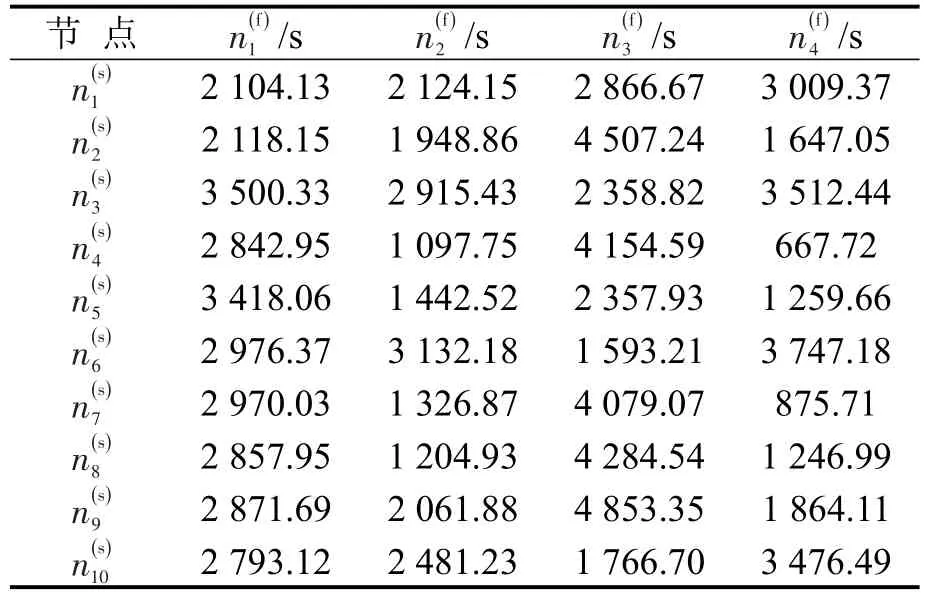
表 5 应急车辆到事故的最短行程时间Table 5 Shortest travel time from emergency vehicles to accidents

表 6 BA_TE算法参数设置Table 6 Selection of parameters of BA_TE algorithm

(3)计算应急车辆调度方案.

采用BA_EVD算法计算最优调度方案，算法参数设置如表9所示.经过图4的寻优过程，获得结果为[1,0,3,2,4,3,4,2,0,3]，解码后获得调度方案如表10所示；与文献[4]中的混合蛙跳算法(Shuffled Frog Leaping Algorithm,SFLA)进行对比，结果如表11所示.

图3 BA_TE算法寻优过程Fig.3 Evolutionary processes of BA_TE algorithm

表 7 疏散后应急车辆到事故的最短时间路径Table 7 Shortest time paths from emergency vehicles to accidents after evacuation

表 8 疏散后应急车辆到事故的最短行程时间Table 8 Shortest travel time from emergency vehicles to accidents after evacuation

表 9 BA_EVD算法参数设置Table 9 Selection of parameters of BA_EVD algorithm

(4)计算结果分析.

①交通疏散效果分析.

对比表5和表8可知，疏散前从应急车辆所在节点到事故所在节点的40条路径中，行程时间超过30 min的达到72.5%，而疏散后该比例下降为42.5%.疏散后行程时间较疏散前缩短139.00～2 070.61 s.表12分析了疏散前后满足事故救援时效的应急车辆数，显然疏散后可用车辆数大幅度增加.

②应急车辆调度结果分析.

BA_EVD算法获得的最优调度方案满足事故的时间窗约束和资源需求约束.由表11可知，对于本文的最小化问题，BA_EVD算法获得的最优解的目标函数值较混合蛙跳算法(SFLA)减小16.85%，运行时间较SFLA算法缩短77.98%.

表10 最优调度方案Table 10 Optimal scheduling scheme

表11 算法性能对比Table 11 Comparison of performances of two algorithms

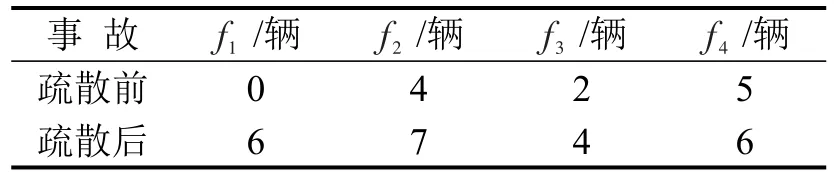
表12 满足事故救援时效的车辆数Table 12 Number of vehicles satisfied rescue timeliness of accidents

4 结论

首先以行程时间、交通负荷和长度等为路段权值，将路网抽象为一个时变有向网络模型；然后，构建双层规划模型描述应急车辆调度和交通疏散间的协同制约关系；接着，设计一种双层蝙蝠算法，通过上下层间的变量传递，实现双层规划模型的求解；最后，采用具有47个节点的路网验证模型和算法的有效性.结果表明：BA_KSP算法能够获得满足路径连通约束的前K条最短路径；交通疏散前后应急车辆节点到事故节点的最短行程时间得到明显降低；BA_EVD算法能够获得满足事故需求约束的优化调度方案，且计算性能明显优于SFLA算法.