考虑前序路段状态的公交到站时间双层BPNN预测模型
2020-05-13王忠宇王艳丽
苗 旭,王忠宇,吴 兵,杨 航,王艳丽*
(1.同济大学道路与交通工程教育部重点实验室,上海201804;2.上海海事大学交通运输学院,上海201306)
0 引言
准确预测公交到站时间不仅可以节约乘客出行时间,提高公共交通吸引力,还有助于运营管理者动态调整运行时刻表和发车间隔,提高运营管理效用.现有预测模型主要包括5种:一是回归模型[1-2],如Chang[1]等开发的临近非参数回归模型,预测公交站点从起点到终点的多区间、多路径的行驶时间;该类模型简单易懂,但精度和适应性较低[3].二是时间序列模型[4-5],如童小龙等[5]考虑站点间行程时间的随机性,利用经验模式把非平稳时序分解为若干平稳时序,并基于二次指数平滑法预测公交到站时间;该类模型预测效果取决于当前交通状态与历史交通状态的偏差,当偏差较大时,预测结果不准确[6].三是支持向量回归模型(Support Vector Regression,SVR)[10-11],如Peng等[10]基于主成分分析法对变量降维,利用遗传算法对SVR参数标定,从而建立改进的SVR模型;该类模型具有很强的学习能力和容错能力,但需对其进行大量训练且耗时较长,难以实时预测.四是神经网络模型[7-9],如罗频捷等[9]将遗传算法和模糊推理系统融入多层前馈神经网络中,建立综合多层前馈神经网络模型;该模型在预测精度上具有绝对优势,但是训练函数、学习函数等参数选择需要经验或试取,也需大量数据训练模型.五是融合模型[12-14],如陈旭梅[12]、于滨[13]等提出的包含卡尔曼滤波及SVR的综合模型,采用SVR模型预测各路段的初始行程时间,将该数据结果作为卡尔曼滤波算法的输入矩阵,实现对公交行程时间的动态预测;该类模型具有较高精度但是也兼顾了所含模型的不足,如卡尔曼滤波模型具有很强的实时性,但仅适用于线性和高斯分布的状态[15],公交到站时间的波动性使得线性状态模型难以描述.因此,有必要合理地设计模型结构,既充分利用机器学习模型(如神经网络及SVR模型)的精度优势,又兼顾模型运行效率.
在模型输入方面,已有研究以星期、天气、路段长度、交叉口数量等静态因素作为到站时间影响因素[16],在复杂交通条件下往往不能取得很好的预测效果.也有学者提出融合道路使用率、车辆平均行驶速度[17]等动态因素.但仅基于公交车辆本身的数据,车速、道路占有率等动态因素难以获得,故充分利用公交车自身数据挖掘运行特征中的有用信息则尤为重要.本文基于大量数据分析,发现目标路段行程时间与前序路段状态有一定关联,考虑前序路段状态可提升目标路段行程时间预测精度.
基于上述考虑,选取预测精度较高的神经网络模型设计考虑前序路段运行状态的双层BPNN(Back Propagation Neural Network)模型进行公交到站时间预测.双层BPNN模型设计将基于静态因素的预测过程提前,简化底层实时预测模型结构,克服以往模型中因考虑多重因素而耗时长的不足.另外,挖掘前序路段行驶状态与目标路段行驶时间的关联性,以期提升模型预测精度.
1 基本设定
1.1 前序路段
以站点作为划分节点,将公交线路划分为若干路段.前序路段指根据公交车辆前进方向,目标路段的上一个路段.如图1所示,A~E代表公交站点,公交车辆行驶方向由A至E,路段Lab为Lbc的前序路段,Lbc为Lcd的前序路段,依次类推.

图1 前序路段示意图Fig.1 Pre-segment diagrammatic sketch
1.2 行驶时间
数据来自公交车进出站GPS数据,车辆抵达及驶离站点时,均会产生包含时刻、站点、车辆编号等信息的数据.可获取车辆在站点的停留时间及站间路段行驶时间.两相邻站点间为一个区间,车辆在区间的运行时间为车辆在站点的停留时间与车辆在路段的行驶时间之和.如图1中区间AB的运行时间为车辆在站点A的停靠时间加路段Lab的行驶时间.
1.3 路段状态相关性
设前序路段状态sa且目标路段状态sb的概率为pab=mabma,其中,ma为前序路段状态a的次数,mab是前序路段状态a且目标路段状态b的次数.pab可表征车辆在前序路段与目标路段行驶状态相关性,在目标路段状态b固定时,如pab不随前序路段状态a的变化而变化,则目标路段行驶状态与前序路段行驶状态无关,否则两者相关.选取部分路段试算pab,计算结果如表1所示.可以看出,车辆在前序路段处于不同行驶状态,在目标路段同一状态出现概率存在差异.如前序路段处于状态0时,约有87%的车辆在龙居路—万德路路段处于状态0;而前序路段处于状态2时,仅有约29%的车辆会在本路段处于状态0.因此,推断前序路段行驶状态与目标路段行驶状态存在相关性.

表 1 前序路段与目标路段行驶状态相关性分析Table 1 State correlation analysis between pre-segment and target segment
2 双层BPNN综合预测模型
2.1 模型总述
提出基于双层BPNN与前序路段运行状态的公交到站时间预测模型.模型计算过程如下.
(1)顶层BPNN模型预测.影响公交行驶时间的静态变量主要包括:起始点编号、时间段(高峰、平峰、低峰)、天气、路段长度、信控交叉口数、节假日、历史均值.本文数据均采集于工作日早晚高峰,故节假日及时间段因素不予考虑,其他因素作为备选变量,如图2所示.采用前向选择法选择最佳变量集,思路为先选一个变量(此处为起始点编号),接着依次向变量集合中添加一个新的备选变量,当新加入的变量使模型性能更优时(此处评价指标为均方根误差减小),则保留该变量,否则不保留.最后基于BPNN模型预测车辆在区间i站点停留时间(ti)与路段行程时间(Ti1),获得车辆到每个站点的初始行程时间.
(2)考虑前序路段状态的目标路段行驶时间预测.利用历史数据基于K-means聚类算法对各路段运行状态划分,利用概率统计法获得前序路段与目标路段间的转移概率矩阵;利用马尔科夫链模型对目标路段行驶时间(Ti2)进行预测.
(3)将顶层BPNN模型的预测值(Ti1),基于前序路段运行状态的预测值(Ti2),同一日之前班次运行时间(Ti3)作为底层BPNN模型的输入,动态预测车辆在目标路段的行程时间(Tip);将Tip代替初始路段行驶时间Ti1,动态调整车辆到达各站点的时间.目标区间的行驶时间为

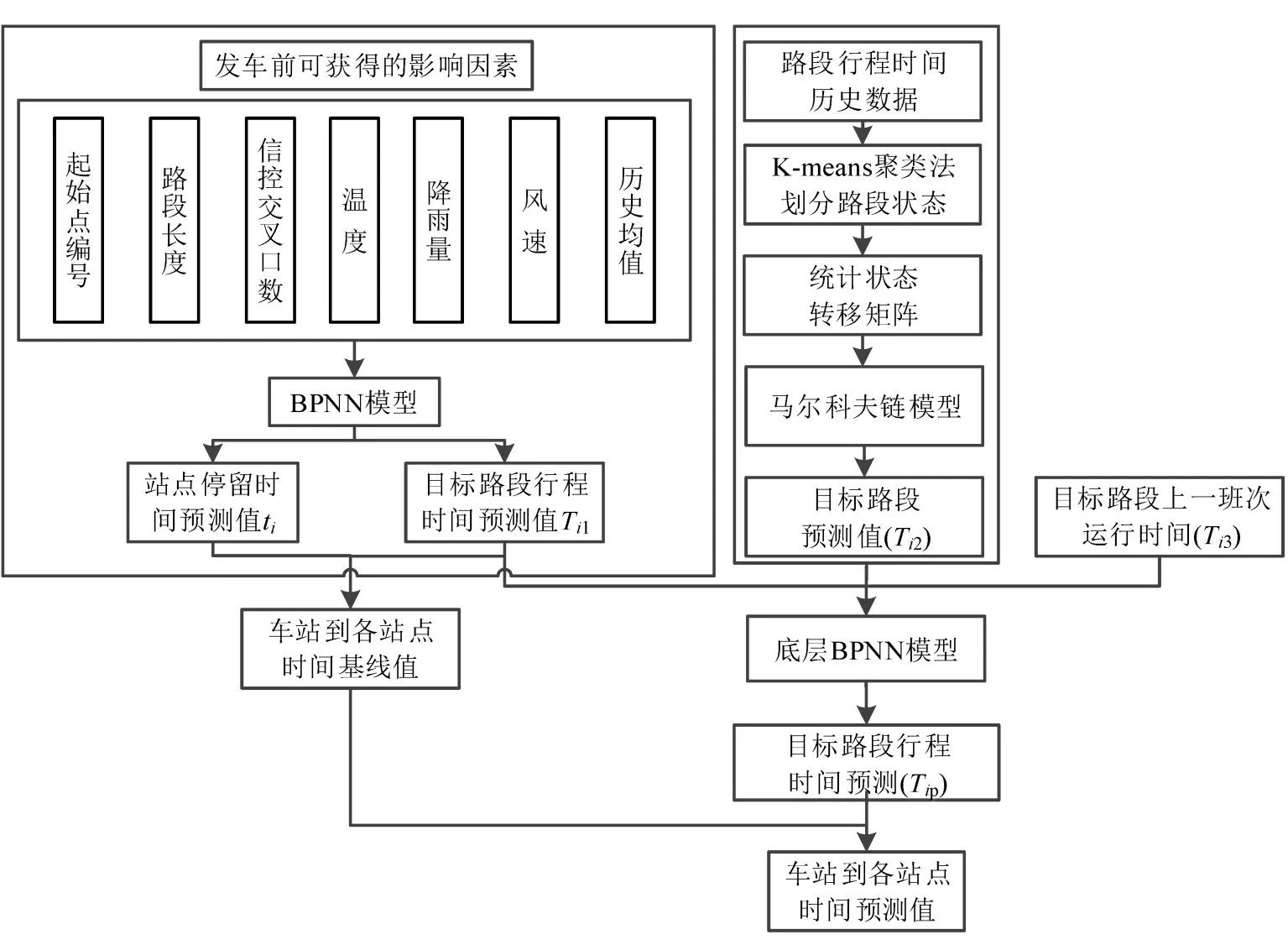
图2 综合预测模型结构图Fig.2 Comprehensive prediction model structure diagram
2.2 考虑前序路段状态的行驶时间预测方法
(1)基于K-means聚类法对公交在各路段的行驶状态划分.通过对车辆行驶时间频次图分析可以看出,部分路段的车辆行驶时间呈现明显的双峰正态分布,如图3(a)所示,此类路段大多仅分布一个信控交叉口,可将路段运行状态划分为2类.而部分路段受到两个甚至多个交叉口的影响,行程时间分布复杂,呈现多峰高斯分布,如图3(b)所示.过多运行状态分类将导致路段某些状态出现的概率极小,故将呈现多峰高斯分布的路段运行状态划分为3类.

图3 路段行驶时间频次分布直方图Fig.3 Road segment travel time frequency distribution histogram
(2)基于马尔科夫链模型预测目标路段行驶时间.基于马尔科夫链基本性质,据前序路段状态可得目标路段行驶时间,公式为
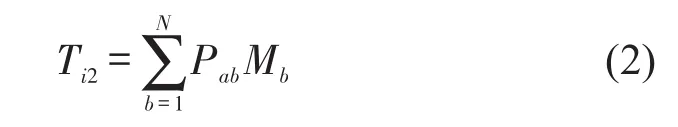
式中:Mb为根据历史数据基于K-means聚类获得目标路段状态b的中心值,N为目标路段状态个数.
2.3 BPNN模型预测算法
双层BPNN模型算法主要设计要素包含网络结构、学习规则和转移函数.
(1)对于网络结构,经测试,两层BPNN模型均采用单隐层就可满足收敛需求,对隐含层分别试验2~6个神经元模式,其中4个神经元模式结果最佳.因此顶层和底层分别构建了7-4-1与3-4-1结构.
(2)对于学习规则,其参数设置是影响模型预测精度的关键因素.其中,学习率、性能函数的研究已较为成熟,采用默认值.最常用的学习函数有动量梯度下降法(traingdm)、自适应梯度下降法(traingda)、有动量和自适应梯度下降法(traingdx)及Levenberg-Marquardt法(trainlm).在其他参数设置完全一致时,对4种学习函数测试,结果如表2所示.4种训练函数的预测精度差别不大,其中,trainlm学习函数训练时间最短,17次迭代便完成模型训练,故采用trainlm学习函数.

表 2 4种学习函数预测结果对比Table 2 Prediction results comparison of four learning functions
(3)转移函数的研究已较为成熟,选择tansig作为转移函数.
3 实例验证
3.1 数据来源
选取上海市791路公交车2015年3月的20天工作日早晚高峰(07:00-10:00,17:00-20:00)数据作为研究对象.公交车在起终点站附近的站点上下车乘客较少,存在过站不停导致进出站数据缺失的现象,故选取第3~26个站点的路段作为模型测试路段.其中,15天的8 884组数据作为模型训练数据,5天的3 036组数据作为验证数据.
3.2 结果对比分析
分别对23个区间行驶时间进行预测,将预测结果与其他模型进行对比.对比模型如表3所示:BPNN-1模型仅考虑静态因素,为本文的顶层模型;BPNN-2为考虑动静态因素的单层BPNN模型;BPNN-3输入变量与BPNN-2一致,但设计为双层BPNN模型,并未对前序路段进行更深层次的挖掘;SVR模型为近几年频繁采用的预测模型.
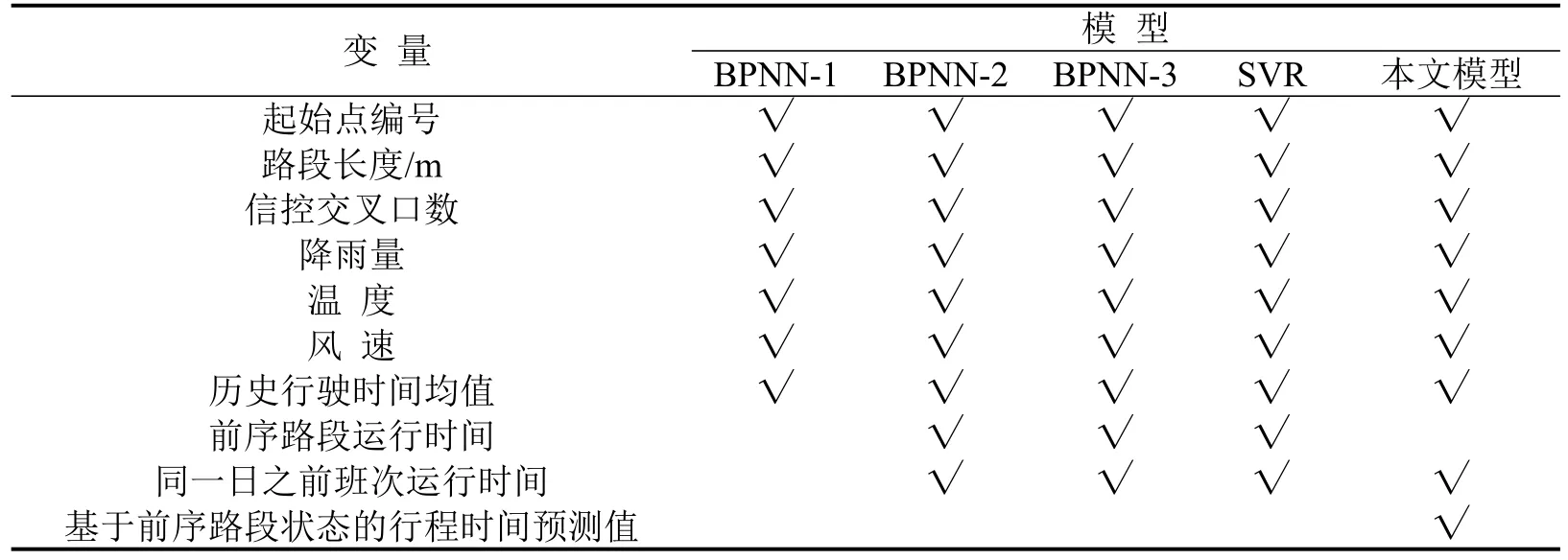
表 3 5种模型变量选择表Table 3 Explanatory variables of five models
模型评价指标采用平均绝对误差(Mean Absolute Error,MAE),平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)及均方根误差(Root Mean Percentage Error,RMSE).
3.2.1 整体结果对比
表4为23个区间的平均预测误差,可看出:①比较BPNN-1与BPNN-2预测结果,仅考虑静态变量的BPNN-1模型预测精度较低;②比较BPNN-2与BPNN-3预测结果,双层BPNN模型预测精度高于单层模型;③BPNN-3与本文模型预测结果对比证明,本文模型更好地挖掘了前序路段与目标路段之间的相关关系,预测精度高;④采用相同输入,SVR模型预测结果略优于BPNN模型,与BPNN-3预测精度相近.
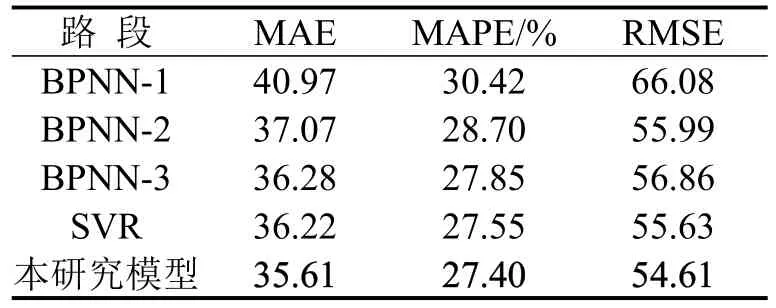
表 4 5种模型预测结果Table 4 Prediction results of five models
3.2.2 雨天结果对比
公交行程时间与天气息息相关,根据是否有雨分成晴天高峰(SP类)及雨天高峰(RP类)两类,AP类为不区分是否有雨的高峰时段,对比3种情况下模型预测误差,结果如图4所示.可以看出,BPNN-1模型、BPNN-2模型及SVR模型受降雨条件影响大,3种模型在雨天预测精度分别降低18.3%、77.93%和50.85%.两个双层预测模型受天气变化影响均较小.图5为雨天5种模型预测精度,可以看出在雨天,本文模型预测精度最高.

图4 不同天气下5种模型预测误差Fig.4 Prediction results of five models in different weather conditions

图5 雨天预测结果对比Fig.5 Prediction results comparison in rainy day
3.2.3 路段误差分析
从路段角度考虑,如图6所示.路段22的MAE与RMSE均最大,分别为91.36 s和146.35 s,原因是其长度远大于其他路段.路段平均长度为0.587 km,路段22为1.1 km,且布设4个信控交叉口,车辆行程时间不确定性更强.本文模型的最大MAPE出现在23号路段,达到39%,主要原因是23号路段仅有215 m,路段行程时间短,故MAPE较大.
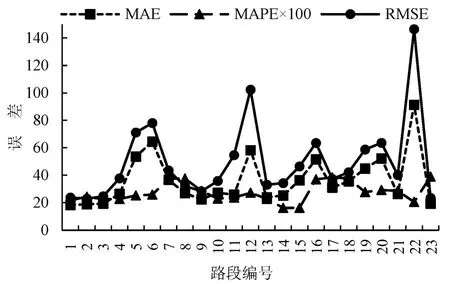
图6 本文模型预测误差Fig.6 Prediction results of model our model
4 结论
充分考虑车辆在前序路段运行状态,提出利用静态变量进行初始到站时间预测,结合车辆实时运行状态动态调整到站时间的双层BPNN预测模型.该模型简化了底层实时预测模型结构,提升了模型预测精度.预测结论主要包括:仅考虑静态变量的模型预测精度明显低于动静态变量综合考虑的模型;提出的预测模型更好地挖掘了前序路段与目标路段运行状态的相关关系,预测精度更高;在雨天,双层预测模型具有更强的稳定性,本文模型比传统BPNN模型精度提升57.25%.
针对上述成果,仍有3个方向值得探索.首先,目前仅选取静态变量预测站台停靠时间,后续可补充公交刷卡数据,提升站点停靠时间预测精度;其次,可补充平峰时段车辆运行数据,对比模型在高峰与平峰时段精度差异;最后,针对部分站点数据缺失情况,可进一步讨论不同数据缺失条件下模型的改进方案.
