考虑博弈的多智能体强化学习分布式信号控制
2020-05-13曲昭伟潘昭天陈永恒李海涛
曲昭伟,潘昭天,陈永恒,李海涛,王 鑫
(吉林大学交通学院,长春130022)
0 引言
实现闭环反馈自适应控制的多智能体强化学习(Multi-agent Reinforcement Learning,MARL)技术为交通网络信号控制领域研究提供了一种新的解决方法[1].Thorpe[2]设计了一种边界恒定流量输入,车辆具有速度随机性的交通模拟器,采用车辆数、信号持续时间、距交叉口距离等因素划分交通状态,并讨论其对SARSA算法应用于路网交通信号控制适用性的影响.Abdulhai等[3]设计了一个泊松到达率的四路交叉口,模拟2 h内不同的高峰状况,采用Q学习对相位顺序和持续时间进行控制并取得良好效果,验证了MARL在交通信号控制上的优越性.Balaji等[4]将借鉴邻近智能体交通数据的改进Q学习方法应用于城市交通干线分布式控制,通过对绿灯时间等参数调节,达到减少总延误的目标.Zhu等[5]在协作多智能体框架的强化学习中嵌入节点树算法用于对交叉口节点最优联合动作的精确推理,调整相序,降低拥堵,减少排放.但文献[4-5]的方法对通信和计算等要求随着路网范围增大呈几何增长,故基于独立动作MARL(Independent Action Multi-agent Reinforcement Learning,IA-MARL)的分布式控制是路网信号控制合理选择.
文献[2-4]中,MARL框架的决策过程多采用贪婪搜索或softmax策略,是建立在其自身累积的历史经验之上进行的,在面临路网中不均衡和波动的交通需求时,反馈控制延迟是不可避免的.若要更好地响应不均衡和波动的交通需求,IAMARL的决策过程应当具有主动应对局部交通状态变化的能力.博弈论中混合策略纳什均衡求解是在不确定竞争条件下求取最优解的方法.局部交通状态变化可视为博弈中的不确定竞争条件,故采用混合策略纳什均衡改进IA-MARL的决策过程是恰当的.
本文在IA-MARL框架的基础上,引入博弈论中混合策略纳什均衡的概念改进IA-MARL的决策过程,针对改进引入JS散度定义自适应学习率,提出考虑博弈的多智能体强化学习(Multi-agent Reinforcement Learning Based on the Game,GMARL)框架,克服IA-MARL只能根据自身历史经验进行决策,不能快速响应路网交通需求不均衡和波动的缺陷.
1 框架提出
1.1 IA-MARL
采用Q因子形式给出IA-MARL中智能体的Q因子更新过程为

1.2 G-MARL框架
为解决IA-MARL面临路网中不均衡和波动的交通需求时反馈控制延迟问题,在IA-MARL基础上,引入博弈过程改进IA-MARL的决策过程,提出G-MARL的框架,如图1所示.
图1给出从道路网络层面到具体交叉口智能体内部G-MARL结构的抽象过程:(I)是道路网络示例,包含6个交叉口,9个出入口,以及其间的双向道路;(II)是道路网络拓扑无向图,节点表示智能体,无向实线表示智能体之间的拓扑关系;(III)是智能体邻近关系拓扑集合简图,每一个邻近关系拓扑图都包含核心智能体(放射无向实线节点)、邻近关系(无向实线)、非邻近关系(无向虚线);(IV)是智能体A4控制逻辑示例,包含3个输入(邻近竞争智能体混合策略集,外界环境的状态,控制动作的回报)和1个输出过程(控制动作);(V)是智能体A4的G-MARL经验更新框架,其中,G-MARL的决策过程在1.3节中说明,G-MARL学习率的自适应设置将在1.4节中介绍.
1.3 G-MARL决策过程
基于Q的IA-MARL的决策过程是在自身经验Q值分布的基础上,采用贪婪策略或玻尔兹曼探索策略对决策做出选择.
图1的G-MARL采用相邻智能体的历史经验Q值分布作为其混合策略分布的估计,通过求解智能体应对相邻智能体混合策略的纳什均衡解,将其作为自身决策的混合策略分布,再在该分布上通过玻尔兹曼探索做出决策.具体过程如下.

图1 考虑博弈的多智能体强化学习(G-MARL)框架Fig.1 Framework of game-based multi-agent reinforcement learning(G-MARL)
(1)相邻智能体的历史经验Q值分布提取.从智能体i的邻近智能体集合I-i中获取邻近智能体j,在面临xj时采用aj的Q值Qj(xj,aj)分布,即

式中:Pj(aj|xj)是智能体在面临xj时选择aj的概率,全部的Pj(aj|xj),aj∈Aj,Aj为智能体j的动作空间,即Pj构成智能体j在面临xj时的混合策略σj,σj∈σ-i,σ-i为临近智能体集合I-i对应的混合策略集合.
(2)智能体i混合策略的纳什均衡求解.在已知对手采用混合策略的预期上,采用混合策略纳什均衡(Mixed Strategy Nash Equilibrium,MSNE)[6]求解智能体i的最佳混合策略为
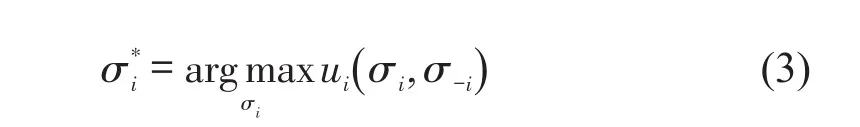
式中:混合策略σi是交叉口智能体i在面临xi时选择控制动作ai在动作空间Ai上的概率分布;是智能体i同对手采用混合策略σ-i的最佳应对混合策略;ui是智能体i的收益函数.
(3)智能体i的决策过程.根据智能体i的混合策略纳什均衡(MS-NE)策略分布,采用玻尔兹曼探索获取智能体i在面临xi时执行ai的概率,即

式中:是改进后得到的智能体i决策混合策略分布.改进后的决策机制可以通过局部的经验交换间接自适应全局的状态变化,进而获取快速适应外部环境波动的能力.
1.4 G-MARL学习率
学习率α值大小与智能体的学习速度相关,α值偏大会对学习积累经验遗忘,α值偏小会产生学习效率下降,这里采用JS散度(Jensen-Shannon divergence)结合1.3节改进的决策过程设置学习率α更新机制,赋予每一个智能体独自的自适应学习率为

根据JS散度定义,展开式(5)为
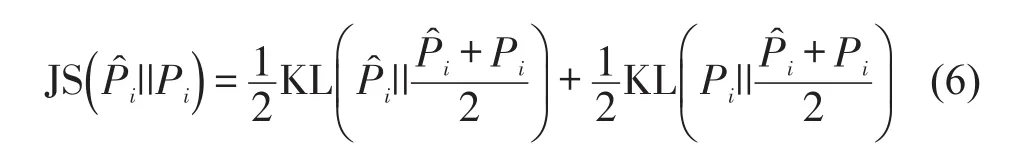

式(6)右侧第2项同样可以采用式(7)的形式求取.这里,式(5)~式(7)中的概率分布见1.3节,Pi是智能体i在动作空间Ai(xi)上的历史经验决策混合策略分布,求解方法见1.3节Pj.
JS散度可以度量概率分布和Pi的距离且具备两种优点:①对称性,②具有固定的值域范围,即[ 0,1 ].根据优点②采用JS散度值更新智能体的学习率是可行的.此外,优点①则可以忽略由于两个概率分布的对比位置带来不对称性的影响,使概率分布之间的差异性得到统一描述.
因此,引入JS散度定义学习率,不仅可以赋予每一个智能体以自适应的学习率,还可以度量智能体自身的历史经验和对局部环境的经验估计之间的差异,使智能体能够自我调节经验更新速度.此外,该方法还能够提升智能体对外部环境变化的敏感度.
2 路网分布式信号控制的参数配置
使车辆在路网中畅通行驶,降低车辆行程时间是路网分布式信号控制的主要目标.为合理验证G-MARL的有效性,避免在路网分布式信号控制应用中状态空间、动作空间划分等定义差异的影响,将用于路网分布式信号控制的IA-MARL和G-MARL相应参数统一定义.受数值模拟计算资源限制,道路网络分布式控制中应用G-MARL和IA-MARL需降低空间复杂度:智能体状态空间(交通状态划分)需要简化,智能体的动作空间(信号控制策略集合)需要简化.
2.1 状态空间划分
假设路网中的信号控制交叉口均为四路交叉口,则智能体i面临的交通状态可用向量表示,进口道d的状态分量表示交叉口d方向进口道的路段交通状态,d∈{e ,w,s,n},e,w,s,n分别表示东、西、南、北进口道,构建公式为

式中:ρd为交叉口d方向进口道路段上车辆数占比;yji为路段lji上车辆数;为路段lji容纳最大车辆数,j∈I-i;free、resistance和jam分别表示自由态、阻塞态和拥堵态3种交通状态.取自由态临界指标φfree=0.5,拥堵态临界指标φjam=0.8对道路面临的交通状态进行简单划分.
2.2 动作空间划分
根据文献[7],动作空间Ai的结构如图2所示,将智能体i在交叉口的控制动作定义为:,即选择行驶方向(道路1、2),同一组不同且不冲突的车流行驶方向(环2)构成的信号控制相位.
这里需要注意的是:G-MARL和IA-MARL均采用无周期无固定相序信号控制优化方式,路网各智能体间隔固定时间并行控制路网中各个交叉口信号相位变化

图2 双环相位结构Fig.2 Phase structure of dual-ring
2.3 收益函数
智能体i面临xi执行ai且邻近智能体I-i面临状态x-i执行联合动作a-i的收益函数为


2.4 回报函数
为实现对智能体i控制效果的评估,智能体i面临xi时执行ai的回报函数ri(xi,ai)定义为智能体i控制交叉口相邻路段车辆数改变值Δyji的函数,即

2.5 其他参数
在G-MARL的应用中,贴现率γ体现了智能体对短期收益与长期收益之间关注程度的差异,本文不针对贴现率进行分析,将其取固定值0.5.
同理,IA-MARL的贴现率也设置为0.5,采用最佳学习率α=0.01.
3 数值模拟实验场景配置及结果分析
实验选用的道路网络结构及在路网中行驶车辆可行路径示意图如图3所示.数值模拟实验通过MATLAB编程实现.采用两种指标评价控制效果:单位行程时间,即车辆在每公里的行程时间(s/km);单位车均延误,即车辆在每公里的延误时间(s/km).

图3 实验路网结构及路径提取示意图Fig.3 Sketch of grid network and travel route
3.1 路网场景选取
合理选用路网规模,既降低计算资源消耗,又充分体现交叉口之间相互作用关系.采用3×3的格子网络作为数值模拟实验中的道路网络,具体结构及节点编号如图3(a)所示.图3(a)中:编号I表示交叉口节点,编号OD表示路网出入节点,各节点之间的无向线段表示双向行驶道路,长度为1 000 m,通行能力为2 400 pcu/h.
3.2 转向比设置
道路网络中,交通流到达情况是随机的,不能简单地采用固定转向比配置各交叉口,故根据OD目的地对转向比进行分析,以图3(b)为例.
(1)获取到的交通流为OD4-OD7;
(2)将OD4-OD7中的可行路段全部提取出来,较远径上的路段用虚线表示,即图3(b)中I;
(3)假设路网中行驶的车辆无绕行行为,避免车辆在路网绕行导致仿真结果偏差;
(4)排除绕路行为路径,用以OD4为起点、OD7为终点的有向无环图(图3(b)中II)表示全部可能的行驶路径;
(5)假设OD4-OD7方向的车辆以等概率行驶在图3(b)中II的3条路径上.
以上述方法,定义OD4-OD7方向车辆在交叉口I2行驶向I3和I5的概率均为0.5.交叉口I的转向比根据各行驶方向车辆的转向累积比例求得.
3.3 输入流量设置
对比G-MARL和IA-MARL方法对交通需求波动的控制效果,在不均衡输入流量的前提下采用泊松到达率作为应用场景.对图2(a)中的格子网络的输入流量进行设置,具体流量流向如表1所示.在表1中,各OD方向的流量为泊松分布到达率输入的均值.此外,以表1流量为基准流量,采用0.5~3.0作为比例系数对输入流量进行调节,进一步分析G-MARL和IA-MARL方法关于流量输入的敏感性.

表1 格子网络各端点OD流量Table 1 OD flow at each endpoint of grid network
3.4 实验结果分析
数值模拟运行3 600 s,为避免路网加载对评价结果造成偏差,剔除1~1 200 s的输出结果.在基准流量输入下,IA-MARL和G-MARL在行程时间和延误方面的控制效果分别如图4和图5所示.关于流量输入变化敏感性,IA-MARL和G-MARL在行程时间和延误上的表现如图6和图7所示.

图4 IA-MARL和G-MARL控制效果对比图(单位行程时间)Fig.4 Comparison of results between IA-MARL and G-MARL(Unit travel time)

图5 IA-MARL和G-MARL控制效果对比图(单位车均延误)Fig.5 Comparison of results between IA-MARL and G-MARL(Unit vehicle average delay)

图6 IA-MARL和G-MARL的流量输入敏感性(单位行程时间)Fig.6 Sensitivity of IA-MARL and G-MARL to flow input(Unit travel time)

图7 IA-MARL和G-MARL的流量输入敏感性(单位车均延误)Fig.7 Sensitivity of IA-MARL and G-MARL to flow input(Unit vehicle average delay)
从图4可见,G-MARL在单位行程时间上较IA-MARL累积改善59.94%.据图5可知,G-MARL在单位车均延误上较IA-MARL累积改善81.45%.分析图6和图7,随着流量输入的增长,G-MARL相对IA-MARL在单位行程时间和单位车均延误方面改善效果均呈现先提升后下降的趋势:①低流量输入,交通需求低,路网畅通,G-MARL的改善效果不明显;②中流量输入,交通需求增长,路网承压,G-MARL改善效果显著;③高流量输入,交通需求接近或超过道路通行能力且不均衡性和波动性降低,路网趋近饱和及过饱和,G-MARL和IA-MARL控制效果相近,微弱改善.验证了GMARL方法能够较好地应对道路网络中不饱和情况下不均衡且波动的交通需求.
4 结论
本文研究交通需求不均衡和产生波动时对应的道路网络信号分布式控制问题,针对IA-MARL决策只依据自身历史经验,不能快速响应路网交通需求不均衡和波动的缺陷,考虑对局部网络交通状态获取,提出基于G-MARL框架的道路网络信号分布式控制方法,设计实验道路网络进行数值模拟仿真.通过仿真结果,分析网络单位行程时间和单位车均延误的变化情况,在路网OD流量输入不均衡时,分析采用IA-MARL和G-MARL的两种分布式控制方法在0.5~3.0倍流量输入条件下对路网的控制效果,验证了G-MARL框架的有效性,即应用基于G-MARL的分布式信号控制能够有效降低车辆在不饱和且交通需求不均衡和波动的城市路网中的单位行程时间和单位车均延误.
