隧道运营期内部空气温度的预测分析

鲁 斌, 蒋 涛, 王树刚, 刘石磊, 尹 龙, 翟康博

(1. 中铁隧道局集团有限公司， 广东 广州 511458;2. 大连理工大学， 辽宁 大连 116024; 3. 中铁隧道勘察设计研究院有限公司， 广东 广州 511458)

0 引言

高地温地质条件不仅会引起洞内气温超过《铁路隧道工程施工技术指南》[1]的相应规定，而且还可能引起衬砌结构热应力异常[2]。随着运营隧道交通量增大，机动车排出的大量热量会导致隧道内空气温度明显升高[1]，因此，获得准确可靠的洞内气温和隧道内壁面温度分布规律，对改善隧道运营环境和采取低能耗的有效降温措施有着很好的指导作用。

隧道内气温预测的理论方法主要有数值解法[2-3]和分析解法[4-5]。周小涵[6]建立了考虑对流-导热耦合作用的隧道温度场有限差分计算模型，分析了隧道内空气温度及围岩温度随入口风温的变化规律； 马国川[7]建立了单线铁路隧道内空气温度的非稳态模拟计算模型，采用有限体积法对热湿控制方程进行离散，并分析得出渗流对铁路隧道内空气及围岩温度的影响规律； 王树刚等[8]同时考虑了矿井通风网络中传质和传热的过程，求解得到围岩振荡温度和振荡湿度的传导方程。虽然针对隧道围岩径向和轴向温度分布混合求解的数值解法有很多报道，但针对解析解的文献报道较少。如邵珠山等[9]利用量纲一化导热微分方程采用莱维法得到了考虑隔热层的高地温隧道温度场理论解，不仅研究了围岩温度沿隧道径向的变化，还分析了其沿隧道轴向的变化，但该分析解受到洞内空气温度为已知条件的限制，没有讨论洞内气温的求解方法。

与数值解法相比，分析解法更为简便、实用，且各种参数对结果的影响规律明确，便于在实际隧道中应用，但目前缺少在求解隧道围岩径向和轴向温度相结合的同时，又能考虑沿隧道轴向变化的洞内气温求解方法。针对当前研究的不足，本文引入传热第三类边界条件，耦合隧道径向及轴向二维轴对称的围岩温度导热方程与洞内气流温度方程，推导出运营隧道内空气温度的分析解，计算得到沿隧道轴向的空气温度，并分析不同风速对出口空气温度的影响。

1 数学模型的描述

1.1 隧道内空气温度的数学模型

隧道模型如图1所示，其中z轴表示隧道轴向，r轴表示隧道径向。考虑沿隧道轴向变化的空气与围岩换热方程[10]，同时为方便推导，做如下假设： 1) 隧道截面等效为圆形断面； 2) 空气以恒定均匀的速度流过隧道； 3) 流体具有恒定的密度ρ和比热cp。所以，能量方程为：

(1)

式中：A为隧道断面面积；uf为隧道内的平均空气流速；Dh为隧道断面当量直径；Tmf为空气平均温度；Tra为隧道内壁面温度；h为空气与隧道内壁面之间的对流换热系数；qsej为单位长度下的散热量；zj为内热源所处隧道轴向位置。

图1 隧道模型示意图

引入量纲一的量如下：

L=l/rb。

(2)

式中：l为隧道长度；Z为隧道轴向的某一位置；T∞为外界无穷远处的空气温度；Tmf0为隧道入口端空气温度；rb为保持原岩温度值不变的围岩外部半径，同时作为长度的量纲一的量的参考值；Tb为rb处原岩温度，同时Tb-T∞作为温度的量纲一的量的参考值。

将式(2)代入式(1)，得到空气与隧道内壁面换热的量纲一的量的温度：

(3)

1.2 围岩温度

由式(3)可知，求解洞内空气温度需要获得围岩温度。在r-z柱坐标系下，设隧道半径为ra，隧道长为l，取隧道一端z=0，考虑隧道两端围岩长期接触外界空气，假定两端围岩温度近似相等(均为T∞)。于是，有围岩温度的基本稳态热传导方程[11]和边界条件如下：

(4)

(5)

式中：Tria(ra,z)表示某一位置处的围岩温度；λ1为围岩的热传导系数。

第1个边界条件即为本文引入的第3类边界条件，对于未明确给出对流换热系数h值的工况，可以根据迪图斯-贝尔特公式(Nu=0.023Re0.8Pr0.4)来估算，得到h的表达式为：

(6)

式中：v为运动黏度系数，取1.516×10-5m2/s； Pr为普朗特数，取为0.729 3。

故第3类边界条件中对流换热h的取值实际为未知参数速度uf的函数。

通过Tmf关联围岩温度和空气温度的表达式，为简化分析，对各变量进行量纲一化：

(7)

将上述量纲一的量引入稳态热传导基本方程及边界条件后，可得：

(8)

(9)

参照文献[12]和文献[13]对空心圆柱体导热的推导过程，引入分离变量法，可以得到Θr(R,Z)的通解：

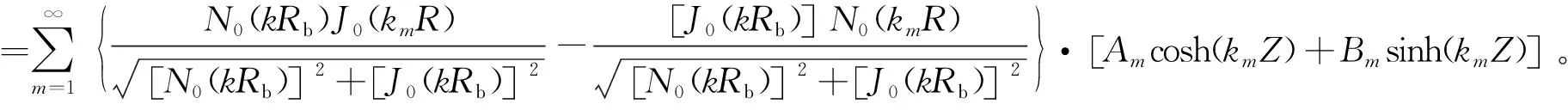
(10)

将式(10)和式(3)同时代入式(9)的前2个边界条件中，经过傅里叶级数变换[15]后，求得式(10)中的系数Am和Bm，于是在式(10)中将R取值为Ra即获得围岩温度Θr(Ra,Z)，再将其代回式(3)，即可得到量纲一的量的空气温度：

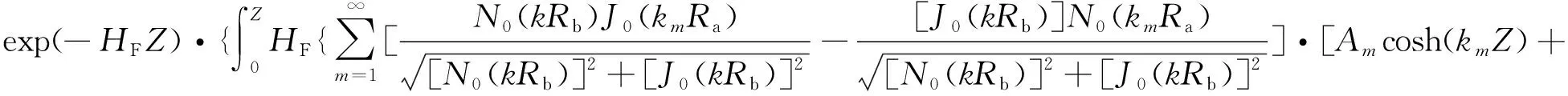
(11)

2 本文分析解验证

2.1 同数值解的比较

文献[16]以大隆矿区矿井通风巷道围岩与巷道风流换热为例，利用数值模拟方法得到了给定计算条件下巷道内的空气温度。计算参数有： 巷道断面面积为6.55 m2，断面周长为9.68 m(当量半径为1.35 m)，巷道总长为2 000 m； 空气热物性参数ρ=1.205 kg/m3，cp=1.005 kJ/(kg·℃)； 巷道岩体热物性参数λ=1.43 W/(m·℃)，巷道内空气对流换热系数h由式(6)计算得到；巷道入口处的空气温度为24.1 ℃，外部原岩温度Tb皆为32.75 ℃。

应用本文分析解计算相同条件下巷道内的空气温度，得到气温随巷道轴向位置的变化曲线如图2所示。由图2可知，巷道入口至出口间的空气温度沿轴向(0 m≤z≤ 2 000 m)不断升高，且随着巷道内平均风速的增加，巷道内气温值不断减小。应用本文式(11)算出的气温与文献[16]最大相差值小于0.5 ℃，且温度变化趋势基本一致，初步验证了式(11)计算结果的合理性。

2.2 同已有实测数据的比较

为了进一步验证式(11)的正确性，需与已有的实测数据进行对比。文献[17]给出了一组武汉长江运营隧道内空气温度的夏季实测数据，该隧道的基本计算参数为： 隧道当量半径为4.4 m，隧道总长为3 260 m； 空气热物性参数ρ=1.29 kg/m3，cp=1.005 kJ/(kg·℃)； 隧道所处地层为砂土层的导热系数λ=1.43 W/(m·℃)，混凝土表面的自然对流换热系数hf=4.8 W /( m2·℃ )； 当地多年平均气温为16.7 ℃，隧道入口处的空气温度为40 ℃，地层稳定温度Tb皆为18 ℃； 隧道内风速uf为5 m/s； 单位长度下车辆散热量、灯具及其他设备散热量为2 054.5 W/m。

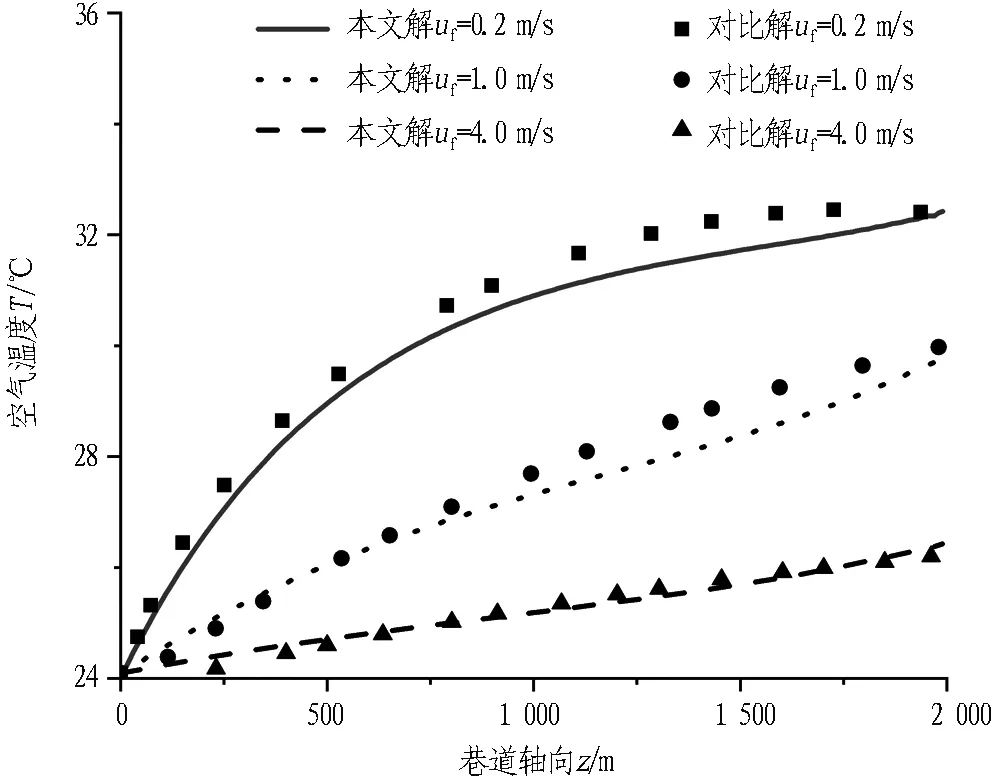
图2 本文分析解与文献[16]数值解的温度计算结果

Fig. 2 Comparison between temperature calculation results by analytical solution recommended and that by numerical solution of Reference[16]

根据以上计算条件，应用本文分析解法计算隧道内空气温度和r=8、14、20 m时沿隧道轴向(0 m≤z≤3 260 m)的围岩温度，并将空气温度的计算结果与实测数据同时绘于图3，围岩温度的计算结果如图4所示。由图3可以看出，隧道内空气温度的计算值和实测值沿着隧道轴向的差值一般在1 ℃以内，最大差值不超过3 ℃，此结果进一步验证了本文分析解的正确性。由图4可以得到，沿隧道轴向的围岩温度在整个隧道中并不完全对称，且靠近隧道出口(z=3 260 m)和内壁面(r=4.4 m)处的围岩温度较高，这皆是空气从隧道入口流向出口的过程中与围岩不断换热的结果。

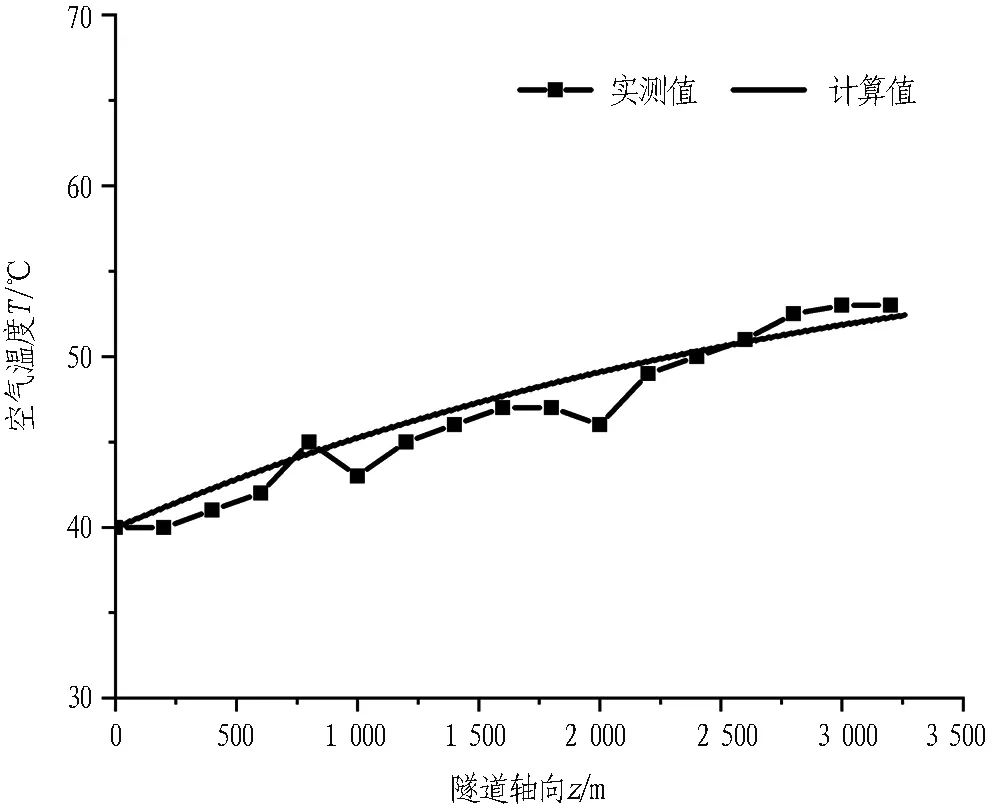
图3 本文分析解计算值与文献[17]实测数据对比

Fig. 3 Comparison between measuring temperature by analytical solution recommended and that by numerical solution of Reference[17]

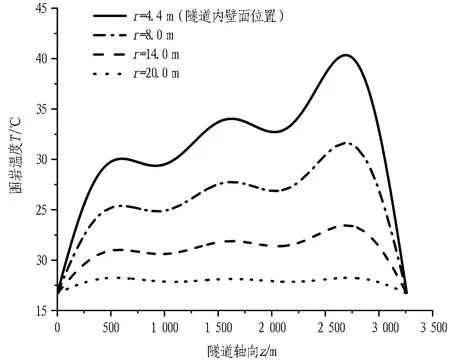
图4 不同轴向距离的围岩温度

Fig. 4 Surrounding rock temperature at different radial distances

3 风速对隧道出口空气温度影响分析

影响隧道运营期内部空气温度的因素有很多，除了有围岩散热外，还有车辆散热量、入口空气温度和风速等。本文将入口空气温度作为边界条件，将车辆等设备散热作为内热源，重点研究隧道运营期机械通风的风流调节作用对空气温度的影响。当自然通风不能满足隧道内气温要求时，需要采取机械风机来调节隧道内的风速，因为风速直接影响了隧道内壁面与空气的对流换热强度，从而对空气温度产生较大影响。根据JTG D70/2—2014《公路隧道设计规范 第二册 交通工程与附属设施》[18]可知，单向交通的纵向及纵向组合式通风风速应控制在1.5～10 m/s，因此本文仍以文献[17]的计算工况为例，其余参数不变，对流换热系数h依据式(6)估算，计算隧道内风速为1.5～10.0 m/s时的出口端空气温度，计算结果见图5。

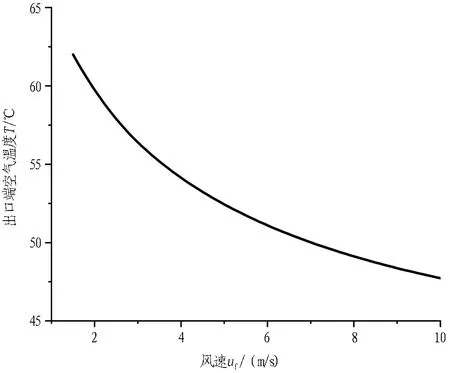
图5 隧道出口端空气温度与风速的关系

Fig. 5 Relationship between air temperature and wind speed at tunnel exit

由图5可知，随着风速增加，隧道出口端空气温度从62.0 ℃降低至47.7 ℃，且下降幅度(风速每增大1 m/s时隧道出口温度降低值)逐渐减小。例如当风速分别为2、6、10 m/s时，对应出口气温随风速增加的下降幅度分别为4.2、1.2、0.6 ℃/(m/s)。以上结果表明，若一味地增加风速来降低隧道内空气温度，那么降温效果随风速增加逐渐不明显，这从降温角度佐证了规范中将风速控制在一定范围内的原因。

4 结论与讨论

本文引入传热第三类边界条件，耦合隧道径向及轴向二维轴对称的围岩温度导热方程与洞内气流温度方程，推导出隧道空气温度和内壁面温度的分析解。通过对比文献报道的巷道内气温的数值解，计算差值在0.5 ℃以内，初步验证了本文分析解的合理性。以武汉长江隧道为例，对运营隧道内的空气温度进行计算分析，并得出以下结论：

1)该隧道的洞内气温计算值与实测值差值大多在1 ℃以内，且温度变化趋势一致，进一步验证了本文分析解的正确性和相应假设的合理性。

2)在式(11)中，对应z=l即可得到隧道出口端空气温度与参量HF的关联式，也就是隧道出口端空气温度与风速uf的关联式。随着风速uf的增加，出口气温不断降低且降幅逐渐减小，即降温效果已逐渐变弱，表明运营隧道内的风速选择应综合考虑降温效果与动力消耗。

3)该解析解考虑了实际运营隧道内被车辆、灯具等热源加热的空气和围岩之间的相互影响，相较于通常不考虑围岩温度沿隧道轴向变化的解析解更加精确，故该解析解可供工程设计人员参考。然而，本文的隧道围岩模型仅考虑单层结构，故式(11)适用于传热介质导热系数相近的情况。下一步应将物理模型扩展到多层隧道结构(衬砌层、隔热层、初期支护层和围岩层等)，推导出隧道空气温度和内壁面温度的分析解。