基于直观想象核心素养的数学课堂教学方式探究——以“指数函数的图像及性质”教学为例

张利贤

一、问题提出的背景

数学是研究数量关系和空间形式的一门科学。数学源于对现实世界的抽象，基于抽象的结构，通过符号运算、形式推理、模型构建等，理解和表达现实世界的本质、关系和规律。数学本身的形成与发展决定数学是一门高度抽象的学科。很多高一学生在高度抽象的数学概念、高度简洁的数学符号、定理、高度抽象复杂的数学问题面前，显得很无助，甚至无所适从，他们不理解它们表示的是什么，这使得学生很难与数学进一步的沟通交流，甚至对数学学习有很大的挫败感。对这一现状，一线数学教师深有体会。在高一数学教学中，经常会遇到简单的(含参)函数问题，学生很难想象其图像的可能性，或不会借助图像来理解和分析问题，这从侧面也反映了高一学生学习数学的核心能力亟待提高。

数学本身是高度抽象的、符号化的，如果教师在教学时，把抽象的数学概念、符号等通过实物模型，几何图形或利用信息技术演示模拟的事物图片等直观地、生动地表达出来，让学生能“够得着”“触摸得到”亲身经历并直观感知，当学生能够直观感知数学问题、数学符号等并能把握其整体结构，那么学生就能理解数学问题，因此学习数学的积极性就会提高。为了帮助学生能利用直观的数学材料来理解数学问题，教师需要加强培养学生几何直观和空间想象的能力，即学生的数学直观想象核心素养。

二、直观想象核心素养

《普通高中数学课程标准(2017 版)》中界定直观想象为：指借助几何直观和空间想象感知事物的形态和变化，利用空间形式特别是图形，理解和解决数学问题的素养。主要包括：借助空间形式认识事物的位置关系、形态变化和运动规律；利用图形描述、分析数学问题；建立形与数的联系，构建数学问题的直观模型，探究解决问题的思路。主要表现是：建立形与数的联系，利用几何图形描述问题，借助直观理解问题，运用空间想象认识事物。可以说几何直观为空间想象提供了认识基础，空间想象为几何直观和由之向整体把握的发展提供了方法，是一嵌套循环的互动关系。

高中数学核心素养是学生在接受高中数学教育过程中，逐步形成适合个人终身发展和社会发展需要的必备品格和关键能力。而高中数学的六大核心素养，落实到每一节课的教学，都会涉及全部和部分。发展学生数学核心素养不是一节两节课或一学期就能完成的，并且每节课的教学，不同的核心素养的培养有所倚重，它需要教师乃至教研组对课程整体统筹规划，对数学知识结构重新重组和优化，明确各单元教学中发展学生数学核心能力的侧重点，在教学设计时，有意识地设计教学活动培养学生的核心素养。

三、探究基于直观想象核心素养培养的课堂教学策略

课堂环节一：画图(从数到形)：在探究指数函数的性质时，由于指数函数的解析式y＝ax(a＞0 且a≠1)过于抽象和笼统，学生难以用解析式来认识指数函数的性质及图像。因此，教师引导学生尝试从特殊底数的指数函数如：y＝2x与研究其图像，从图像直观感知其图形的形态变化。学生在面对特殊底数的指数函数解析式y＝2x与时，也无法清楚其图像和性质。教师引导学生从探究其图像出发，学生根据已有的作图经验和方法(列表、描点、画图)画出图像。学生经历作图的过程，从离散的坐标点(数)到几何图形(形)，直接接触和感性认知y＝2x与的图像。

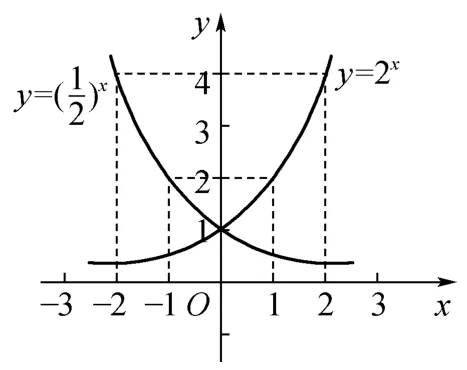
图1

课堂环节二：看图(感性认知)：教师通过问题引导学生观察图像。问题1：请同学们观察图1，你发现了什么?函数y＝2x的图像和的图像有什么关系?可否利用y＝2x的图像画出的图像?引导学生从整个坐标系中两个函数图像的位置关系，到单一函数图像的形态变化(从左向右看图像的变化趋势)进行观察。学生观察，总结结果：图像的位置关系：这两个指数函数(底数互为倒数)图像关于y轴对称，他们相交于点(0，1)；图像形态变化为：从左向右看：y＝2x的图像是上升的的图像是下降的。让学生从画图到直观看图，是为了让学生对两个函数图像有一个直观感性的认知。

课堂环节三：识图(理性认知)：问题2：请同学们仔细观察列表和图像，请解释为什么y＝2x与y＝的图像关于y轴对称?同学们根据列表的坐标和解析式发现，这两个底数互为倒数时，解析式可以表达成y＝2x与，即任意给自变量互为倒数时，其对应的函数值相同，在坐标系中表现为这两个坐标点关于y对称，学生通过直观图像的感性认知，再通过对解析式分析，发现底数互为倒数的两个指数函数图像关于y轴对称的本质属性即它们坐标关于y轴对称，培养了学生通过直观感性认识问题到理性认识问题的意识。

通过从感性到理性认识的不断深入，教师设计问题3：如果我们改变底数a，那么指数函数图像又有什么特点与变化规律?让我们在同一个坐标系再画y＝3x与的图像。通过信息技术：希沃白板画出其函数的图像。教师引导学生从图像的位置关系和形态变化及运动规律识图：图像的共同特征(整体感知)，不同特征(从形到数，从数到形)(图像从左向右看，图像随着自变量x变化，图像如何变化)，同侧图像相对位置变化趋势。通过引导学生识图，从直观感知图中4 个函数图像整体变化规律到理性认知他们内在关系。总结出规律：共同特征(整体感知)：图像都经过(0，1)点，从解析式看出，当x＝0，恒有y＝a0＝1(a＞0 且a≠0)，找到其本质特征；图像都在y轴正半轴，从解析式看，对任意x∈R，y＝ax(a＞0 且a≠0)恒正，学生通过观察图形(形)的特征，结合解析式(数)的分析，理解指数函数的值域都是大于零，这里培养学生数形结合的意识。不同特征：当a＝2 和3(a＞1)时，从左向右看，图像变化趋势相同，都是增的趋势；当(0＜a＜1)时，从左向右看，图像变化趋势相同，都是减的趋势。同侧图像的相对位置变化趋势：当a＝2 和3(a＞1)时，底数a越大时，图像约靠近y轴(0＜a＜1)时，底数a越小时，图像约靠近y轴。通过直观感知图形的变化，再到解析式分析理性认识特殊指数函数的性质，学生经历了感性认识到理性认识的过程。

通过图2 的分析和总结规律，问题4：让同学猜测y＝10x的图像可能是怎样的?在同一坐标系中，如图2 是黄色的曲线还是黑色的曲线?学生对前面4 个函数的图形的位置关系，形态变化进一步地从感性认识上升到寻找出其规律的理性认知，通过问题4，又让理性认识(规律)到猜测y＝10x图形的感性认识(图形)，即感性到理性再到感性，经过一系列的循环，每一次认识达到高一级别的认识，从而整体把握了四个指数函数的图像及性质。学生根据已有的认知经验，在脑中创造出所需要的形象即是y＝10x的图形表象，猜测出y＝10x的图形，同时也想象出y＝的图形表象，通过希沃白板画出具体图形验证学生通过已有经验，大脑想象出图像表象的正确性，这也极大地鼓舞了学生学习的兴趣。这个过程是教师引导学生从借助几何直观和空间形象来认识指数函数图像的空间的位置关系、形态变化和运动规律的看图识图，通过感性到理性再到感性认识过程，发展学生的直观想象能力。

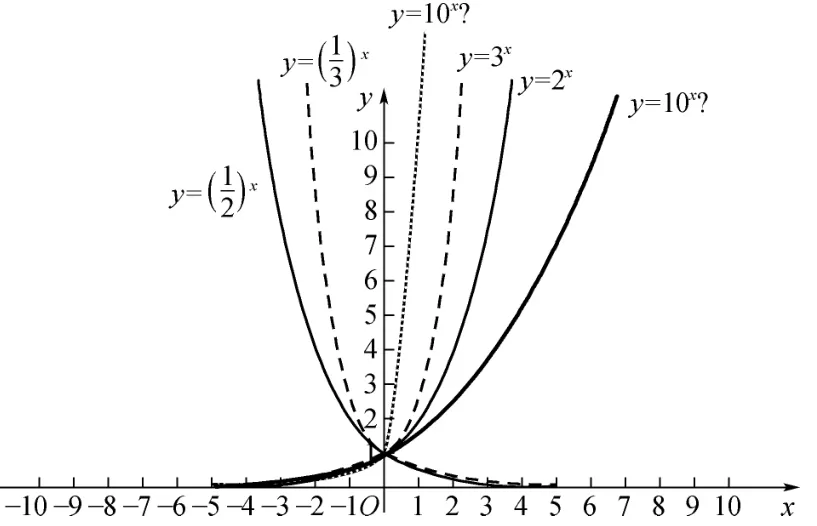
图2

课堂环节四：学生经历了特殊底数的指数函数图像及性质的探究，通过希沃白板探究了6 个指数函数的图像，学生通过感性认识到理性认识再到感性认识等整体把握6 个函数的几何图形的变化规律，学生通过已有知识经验和感性材料，通过大脑想象出一般的指数函数y＝ax和(a＞0 且a≠1)，底数a变化，其图像的直观模型的可能性，教师借助希沃白板演示指数函数图像随着底数a变化的图像，一方面验证学生头脑想象的图形表象，另一方面，再让同学们进一步直观感知一般指数函数的图形形态变化和运动规律，为学生提供更多的感性的材料。学生利用图像的观察和图形描述，通过借助研究函数的科学方法分析指数函数的解析式y＝ax和(a＞0 且a≠1)，抽象并构建出指数函数当0＜a＜1 和a＞1 两类直观图形模型，学生通过动态的几何图形变化，通过感性到理性再到感性再到理性等一系列循环认知过程，整体认识指数函数的性质。

课堂环节五：用图(构建数学问题直观模型，探索解决问题的思路)：课堂问题探究：求函数f(x)＝3｜x｜＋1 的值域。学生原有的认知是脑海中有指数函数的图像和性质，但是没有f(x)＝3｜x｜＋1 的图像，学生对此问题没有什么思路。教师有意识地引导学生先分析解析式，然后看看能不能画其图像，通过图像寻找解决问题的思路(数形结合)。学生通过对f(x)＝3｜x｜＋1 分析得f(x)＝，对分段函数画图，构建了问题的直观模型，通过直观模型，学生很清楚f(x)＝3｜x｜＋1 性质，解决此问题的思路跃然纸上。例如：试比较大小这样的问题，鼓励学生在脑中构建y＝2x和y＝0.6x的具体直观模型，通过探索函数的单调性，寻找解决问题的思路。如何构建数学问题的直观模型，要求，教师在数学教学时，要多培养学生的数形结合的能力；课堂探究数学问题时，多培养学生应用几何直观和空间想象思考问题的意识；在课堂例题和练习时，多培养学生作图(精图，简图)的习惯，构建数学问题直观的数学模型，让学生在具体的情境中感悟数学的本质。本节课的学习，学生基本能根据指数函数的解析式熟练地画出简图，能根据图像写出指数函数的解析式，会对照指数函数的图像直观地得到性质，达到课标的要求。

总之，培养学生的直观想象素养需要教师在教学中，为学生提供大量的直观感性材料，并且让学生认真仔细地观察和较为深入长久的分析与思考、经过学生头脑对这些感性材料表象的抽象和概括、记忆和联想、对比和加工、学习画正确、标准的直观想象平面图、用文字和语言准确描述直观想象图或动态过程(如指数函数的图像与性质的探究，学生对特殊和一般函数的图像进行抽象概括，记忆和联想等一系列感性理性循环认知，最终达到认识指数函数的图形和性质的目的)，逐渐积累丰富的直观想象方面的数学经验，促进直观想象素养的形成。