由一道习题引发的教学思考

徐丽珍

学生总是匆忙完成作业，不多加以思考、探究，往往忽略了问题本质，就题解题的学习态度。如果一线教师碰到此类问题，不加以挖掘问题本质，那么就太浪费教学资源，因此，一线教师不光要加以重视学生存在困惑，还要引导学生进行探究问题，从初识问题、认识问题到深化问题，使得学生能悟出此类问题本质，并加以理解，让学生在此类问题的解决上有所突破。

一、背景展现、发现问题

这是一道高一的习题：

题目：在△ABC中，设

(1)求证：△ABC为等腰三角形；

答题分析：答(1)没有问题。(2)学生答的不理想：①答题的正确率不高，部分同学是空白的，表现为没有想法；②做了的同学，方法选择比较烦琐或者计算错误；③选择较好的解题方法的同学很少。因此，面对这样的一种教学现状，直接提供好的方法，显然不对。数学的学习是数学思维的形成过程，需要学生能从本质上认识此类问题，在解题上需要实现优化解题思路、简化解题过程，值得探究。

二、初识问题，探究模型

学生错误是学生对基础知识还不够落实，基本技能不太掌握，因此高中数学解题教学应以“基础知识的掌握、基本技能的提高、基本思想方法的落实”为原则。在教学中，教师不是直接告诉学生，而是通过问题设计，充分激发学生的思维，学生能自然地感悟到知识的形成，然后寻找问题与知识间的联系，会对学生分析问题产生积极的影响，开阔了解题的思路。

例(2012·浙江15)在△ABC中，M是BC的中点，AM＝3，BC＝10，则

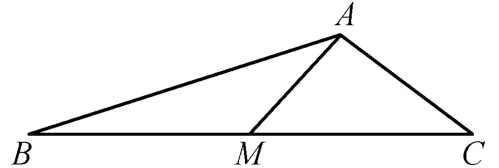
这类问题的特殊性就是极化恒等式，但是从解题的情况来看，学生只是恰巧碰对了，未能真正理解极化恒等式的本质。

【设计意图】例1 的设计让学生能简单认识极化恒等式是用基底表示数量积运算的一种应用，是对基础知识的简单深化。由于条件与结论之间的关系紧密，学生很容易突破问题。

三、认识问题，探究本质

我们知道，向量加法的三角形法则和平行四边形法则本质是一样的，那么你能从平行四边形的角度看极化恒等式吗?

学生：已知平行四边形ABCD中，对角线交于O点，则

即在平行四边形模型中，我们求共起点的两个向量的数量积，只要知道哪些量就能求呢?

学生：我们只要知道这两个向量为邻边的平行四边形的两条对角线的长；

很好，我们把这个模型称为极化恒等式的平行四边形模型；

很好，这个式子就是极化恒等式的符号表示式；

那么，前人是怎么发现极化恒等式的呢?大家请看一个我们都熟悉的问题。

题目：平行四边形是表示向量加法与减法的几何模型。你能用向量方法证明平行四边形的对角线的平方和等于两条邻边平方和的两倍吗?

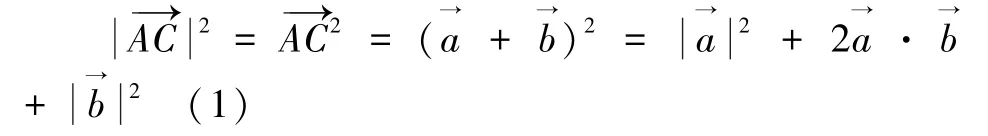
你能发现这个问题的背景与极化恒等式的联系吗?

这个时候，学生的眼神会告诉我们，如果在碰到这个问题时，能够再细心一点，或许就能发现极化恒等式。

请同学们归纳极化恒等式的表现形式；

她是你的煞星！你要做的，是将刀插入她的心脏！不能再继续犹豫和顾虑，这只会让你更加得软弱，更加得无法握住刀柄！

追问：极化恒等式解决什么问题?

学生：极化恒等式描述的是两个数量积、这两个向量的和的模和这两个向量差的模的关系；

【设计意图】寻找知识点并重构对知识的再理解，使得知识的内涵得以丰盈，使知识的展开、方法的形成不再是无本之木、无源之水。学生能够更加系统地认识到问题是源于课本而又高于课本的一种现象，这样使得学生能够更好地认识问题。

题目：在△ABC中，设

(1)求证：△ABC为等腰三角形；

经过这一系列的努力，学生解(2)小题不再是构造函数思想来求了，学生能分析出设O为AC的中点，即，是个常量，在△ABC中，OC随着角B在变换，

【设计意图】学生通过错误题目的再探，自然地解决问题，能让学生深刻体会细细研究问题的重要性，对模型的认识到位，自然出现最优的解法，增加学生的解题兴趣。

辨析：虽然我们都用的是三角形模型的极化恒等式求数量积的范围问题，但是只能是中线是变量吗?

学生：利用极化恒等式求解数量积的问题，化归思想是转化为两个线段的长度问题，若其中一个是变量，就可以探究这个数量积的范围问题。

老师：答得很好，在一定程度上我们认识了使用极化恒等式的特点。

变式1

学生：设DB的中点为E，，此时，学生有些困惑，因为这两个量都随着D在变换，不能求出的取值范围。

追问：使用极化恒等式有什么要求?

学生：使用极化恒等式的化归思想，要转化为已知的线段长或者已知一个变量，若两个都是变量，就不能使用了。

追问：那么此题的数量积怎么求呢?

【设计意图】通过变式1 的辨析，学生更清楚极化恒等式的化归思想的应用，进一步认识了极化恒等式的本质，同时也明白极化恒等式求数量积不是万能的。

四、深化问题，提升素养

变式2：(2013·浙 江)设△ABC，P0是边AB上一定点，满足，且对于边AB上任一点P，恒有则( )

A.∠ABC＝90° B.∠BAC＝90°

C.AB＝ACD.AC＝BC

【设计意图】通过真题检验，希望同学们能够增强学习信心，深化了对极化恒等式的本质的理解。进一步证明高考就是对高于课本的知识考查，让学生碰到问题能更好地去研究问题，提升学生解题的能力，实现何以知其所以然的解题境界。

五、教师反思，感悟提升

大部分学生在平时解题时，只是匆忙地完成解题，没有养成探究问题的习惯，这样的数学学习只能在题海战术中摸爬滚打，这样学生学得很累，没有达到高效课堂的效果。碰到这种情况，如果教师能以学生存在的问题作为备课的主题，在课堂中引导学生以问题和变式为载体，从中发现他们的共性，能让学生抽象出一般的数学问题，从而建立数学模型，然后能让学生进一步深化理解和应用辨析，掌握模型的本质和模型的应用，从而深化对模型的理解，最后达到真正的领会和掌握，这样，就能到达从一道题到一类题的过渡，达到课标要求。通过高中数学课程的学习，学生能提高学习数学的兴趣，增加学会数学的自信心，养成良好的数学学习习惯，发展自主学习的能力。罗增儒教授指出：谁也无法教会我们解所有的数学题，重要的是，通过有限的学习去领悟那种解无限道题的数学素养。