2,6-二氨基-3,5-二硝基吡啶-1-氧化物基PBX的热安全性研究

何志伟，王 洋，刘 锋，郭子如，程 奥，刘祖亮

(1.安徽理工大学化学工程学院，安徽 淮南 232001；2. 南京理工大学化工学院，江苏 南京 210094)

引 言

现代战场上要求弹药在具有高威力的同时，在作战和生产、贮存、运输过程中也要有较高的安全性。世界各国逐渐将高能钝感炸药作为弹药发展的重点，TATB、NTO、LLM-105等多种钝感炸药相继问世。由于这类炸药生产成本高、精制较难、性能不稳定，未得到大范围推广应用。2,6-二氨基-3,5-二硝基吡啶-1-氧化物(ANPyO)是一种新型耐高温单质炸药，性能与TATB相近，但其成本更低廉，合成精制更简单，因此在高聚物黏结炸药(PBX)中具有广阔的应用前景[1-3]。1995年由Ritter-Licht[4]首先提出硝化、氧化2，6-二氨基吡啶合成ANPyO的方法，随后受到国内外广泛关注。周心龙等[5-6]对ANPyO进行分子动力学模拟，研究了ANPyO结构、能量和力学性能及其温度效应，从理论上揭示了其力学性能随温度递变的规律。成健[7]、张蓉仙等[8]对ANPyO复合材料的制备和性能进行了研究，并对其热分解过程进行了分析。

上述研究限于ANPyO单质或复合物的热分解行为和性能研究，为了表征ANPyO应用于高聚物黏结炸药的热安全性，并确定合适的黏结剂体系，本研究根据ANPyO耐热钝感的特性，基于氟橡胶F2311和丁腈橡胶NBR-26设计出两种黏结剂体系，分别制备两种ANPyO基PBX。通过扫描电子显微镜(SEM)、差示扫描量热法(DSC)和热重分析法(TGA)分析两种不同黏结剂体系PBX的结构和性能，根据热力学参数、热安全性参数和热感度概率密度函数，初步评价其热安全性，为该化合物在耐高温炸药的应用提供必要的理论基础。

1 实 验

1.1 试剂与仪器

ANPyO为实验室自合成，亮黄色粉末，理论密度为1.878g/cm3；丁腈橡胶NBR-26，为丁二烯和丙烯腈共聚制成的合成橡胶，为黄色黏性固体。氟橡胶F2311，为偏氟乙烯与三氟氯乙烯的共聚弹性体，为乳白色半透明固体。采用水悬浮溶解蒸馏法制备ANPyO基PBX，以丁晴橡胶NBR-26为黏结剂体系主体的ANPyO基PBX记为样品1，以氟橡胶F2311为黏结剂体系主体的ANPyO基PBX记为样品2。

VEGA3 SBH型钨灯丝扫描电子显微镜，美国TESCAN公司；TGA/DSC3+型TG-DSC联用差示扫描量热分析仪，瑞士METTLER TOLEDO公司。

1.2 实验方法

扫描电镜实验：采用钨灯丝扫描电子显微镜进行分析, 以20kV能量的电子束作为微束激发源，将样本用金钯合金喷镀，高真空条件下进行SEM检测并选取具有代表性的区域拍摄。

热分析实验：通过TG-DSC联用差示扫描量热分析仪，测量热流和试样质量变化。动态气氛N2，气体流速为30mL/min；升温速率(β)分别为2.5、5、7.5、10K/min；升温区间为303.15～773.15K。

2 结果与讨论

2.1 微观形貌表征

用扫描电镜(SEM)对ANPyO基PBX样品1和样品2的微观形貌进行观察，放大倍数为1000倍，结果如图1所示。

图1 ANPyO基PBX的微观形貌

由图1(a)可知，被NBR-26黏结剂包覆后的ANPyO颗粒表面较为光洁，形状无规则，NBR黏结剂颗粒较为细腻，对ANPyO包覆较为紧密；由图1(b)可知，被F2311黏结剂包覆后的ANPyO颗粒表面棱角较多，形状无规则，F2311黏结剂颗粒较为粗糙，对ANPyO包覆效果不佳。SEM分析结果显示，ANPyO大颗粒表面附着许多不规则的结晶，高聚物在晶体颗粒的表面形成一层很薄的膜，可以包覆隐藏晶体颗粒上的尖锐棱角。包覆后大颗粒表面的黏结剂薄膜减少了ANPyO颗粒间的接触，缓冲外界机械作用，有利于改善材料的安全性能。NBR黏结剂体系对ANPyO颗粒的包覆效果略优于F2311黏结剂体系。

2.2 热分解性能分析

样品1和样品2的DSC实验数据如表1所示，其中升温速率为2.5K/min时的DSC和TG曲线如图2所示。

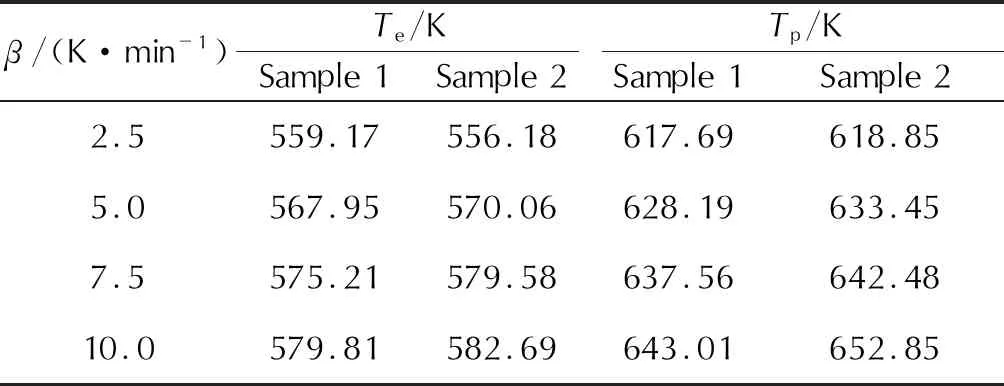
表1 样品1和样品2的DSC实验数据

注：Te为外推起始分解温度;Tp为峰值温度。

由表1可知，样品1的起始分解温度在559.17～579.81K，放热峰值温度在617.69～643.01K；样品2的起始分解温度为556.18～582.69K，放热峰值温度在618.85～652.85K。NBR-26和F2311对ANPyO热分解温度作用效果相近。

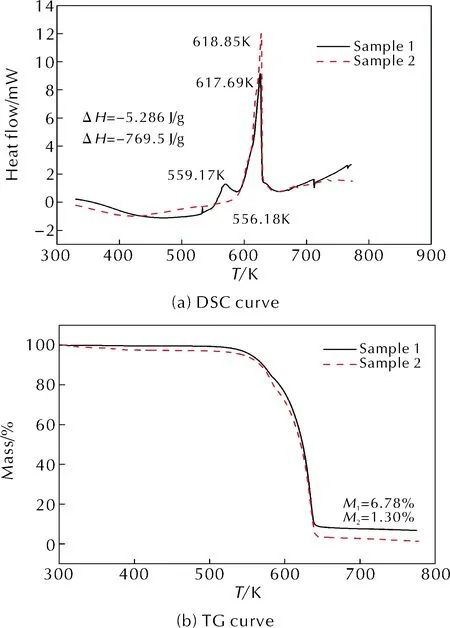
图2 升温速率2.5K/min时样品1、样品2的DSC和TG曲线

由图2可知，样品1和样品2的热分解过程均有一个较强的放热峰，均没有融化吸热过程，其中样品1在热分解起始阶段存在放热峰，初步推测是丁腈橡胶中微量丙烯腈热分解放热产生。样品1和样品2的起始分解温度分别为559.17和556.18K，放热峰值温度分别为617.69和618.85K，分解热分别为528.6和769.5J/g；样品1和样品2的反应残渣率分别为6.78%和1.30%，样品2反应更为彻底。对比纯ANPyO的分解热可知[3]，F2311黏结剂体系参与ANPyO基PBX放热反应，可大幅度提高炸药能量释放程度，NBR黏结剂体系对提高PBX能量释放程度影响不明显。

2.3 热分解动力学计算

将DSC实验得到的Te和Tp(见表1)代入Ozawa方程和Kissinger方程[9-11]，见方程(1)和方程(2)，计算结果如表2所示。对比EOe和Ek相差很小，说明样品1和样品2在转化率α为0～1的范围内遵循同一个反应机理。

Flynn-Wall-Ozawa方程：

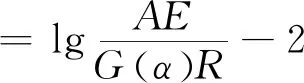
(1)

Kissinger方程：

(2)

式中：A为指前因子，s-1；α为炸药反应深度；β为升温速率，K/min；E为活化能，kJ/mol；R为理想气体常数，J/(mol·K)。

样品1和样品2热分解的TG实验数据如表3和表4所示。在2.5、5.0、7.5、10K/min的升温速率下，将由TG实验得到的βi、Ti和αi，i=1、2、3…代入Ozawa方程，计算所得表观活化能EO的值列入表3和表4中。Ozawa方程计算所得EO值变化较小，且与上述计算结果相近。因此，在该区域内研究物质的热分解机理是可靠的，通过Ozawa法计算得到的EO值是否稳定是检验分解机理一致性的标准。

将单一TG的α—T数据代入到方程(3)～方程(6)[9-11]中得到ANPyO基PBX的E、A和动力学机理函数。

表2 由DSC实验数据计算所得样品1和样品2的动力学参数

注：EOe为不同Te下由Ozawa方程计算得到的活化能；EOp为不同Tp下由Ozawa方程计算得到的活化能；Ek为不同Tp下由Kissinger方程计算得到的活化能。

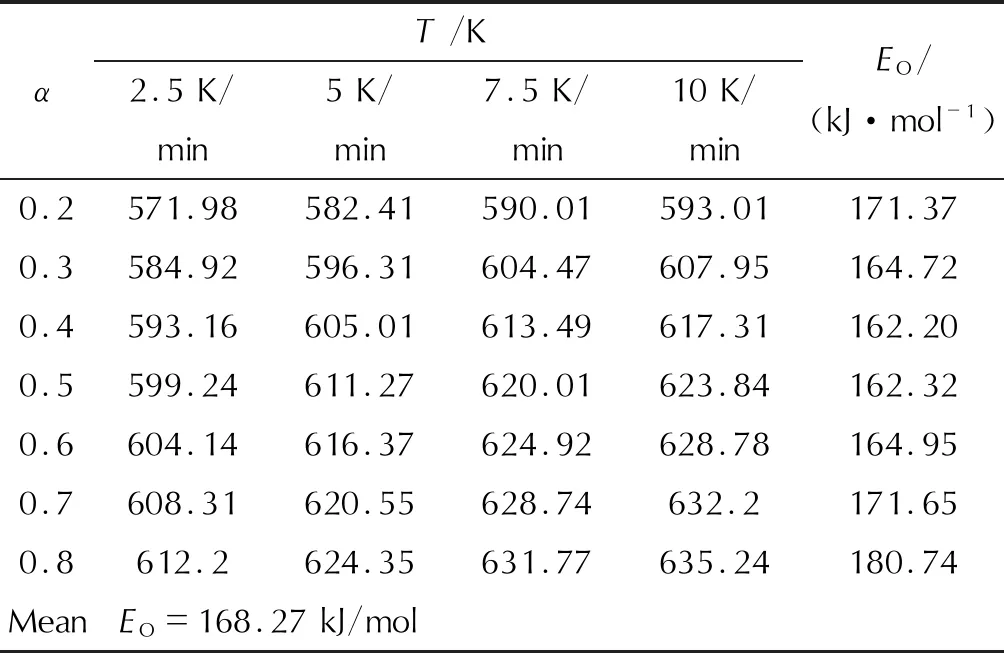
表3 样品1在不同加热速率(β)下TG实验数据和活化能(E)计算结果

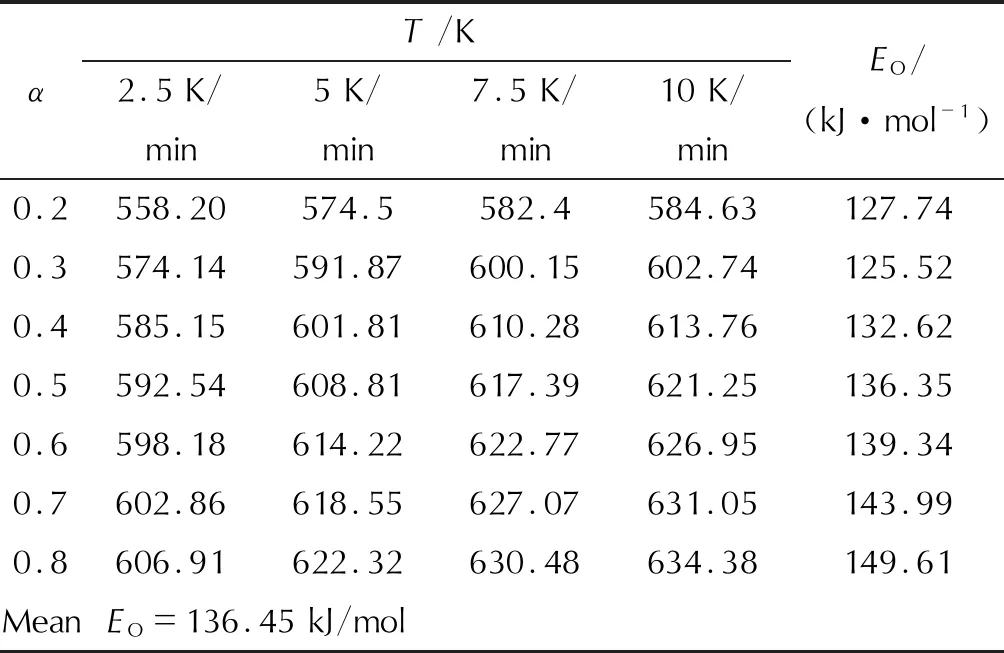
表4 样品2在不同加热速率(β)下TG实验数据和活化能(E)计算结果

Satava-Sestak方程：

(3)

The Universal Integral方程：

(4)

Agrawal方程：

(5)

Mac Callum-Tanner 方程：

(6)

将常用的41种动力学机理函数和在不同升温速率下α—T数据代入到方程(3)～方程(6)中计算，用线性回归处理和逻辑选择法确定样品1和样品2放热分解反应的动力学参数，计算结果取平均值，与表3和表4的E、A值基本一致，由此确定样品1和样品2放热分解的动力学机理函数。其中，样品1的活化能E=173.19kJ/mol，指前因子ln(A/s-1)=28.58；样品2的活化能E=143.78kJ/mol，指前因子ln(A/s-1)=22.89；样品1和样品2热分解的动力学机理函数积分式均为G(α)=[(1+α)1/3-1]2，微分式均为f(α)=3/2(1+α)2/3[(1+α)1/3-1]-1，将样品1和样品2的活化能和指前因子代入方程(7)：

(7)

得到NBR黏结剂体系ANPyO基PBX热分解放热过程的动力学机理方程为：

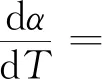
(8)

得到F2311黏结剂体系ANPyO基PBX热分解放热过程的动力学机理方程为：

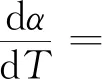
(9)

2.4 比热容cp和导热系数λ

ANPyO基PBX主体成分为ANPyO，其他添加物含量较低，样品1和样品2比热容cp和导热系数λ可由纯ANPyO近似得到。由理论公式(1)和公式(2)可计算得到ANPyO的比热容，将ANPyO的摩尔质量M=215g/mol代入公式(10)和公式(11)。

(10)

cP=0.8cV

(11)

式中：R为摩尔气体常数，8.314J/(K·mol)；a、b、c和d分别为ANPyO分子式中C、H、O和N的原子数，其值均为5。计算得cp=0.998J/(g·K)。

将ANPyO的比热容cp=0.998J/(g·K)，密度ρ=1.878g/cm3，摩尔质量M=215g/mol以及熔点Tm=627.15K[6]，代入公式(12)，可得：

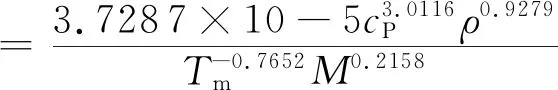
(12)

ANPyO的导热系数λ=0.2882W/(m·K)。

2.5 自加速分解温度及热爆炸临界温度

由方程(13)[12-14]可获得β→0时，样品1和样品2的外推起始分解温度Te0及峰顶温度Tp0，其中以β→0的Te0值视为试样的自加速分解温度(TSADT)，计算结果见表5。

i=1,2,3,4

(13)

式中:η1、η2和η3为系数；βi为加热速率，K/min；Tei为外推始点温度，K；Tpi为热分解峰温，K；Te0和Tp0分别为当β→0时对应的外推始点温度和热分解峰温度，K。

由方程(14)[12-14]，代入外推起始分解温度Te0和EOe，可计算获得样品1和样品2的热点火温度Tbe；代入峰顶温度Tp0和EOp可计算获得样品1、样品2的热爆炸临界温度Tbp。计算结果见表5。

(14)

式中：EOe or Op是由Ozawa法计算得到的活化能(表2)，kJ/mol；Te0和Tp0分别为外推始点温度和热分解峰温度，K。

表5 样品1和样品2热爆炸温度计算结果

2.6 热感度概率密度分布函数

为阐明样品1和样品2对热的敏感程度，对比NBR黏结剂和F2311黏结剂对PBX热安全性的影响[12-17]，由公式(15)～公式(19)计算样品1和样品2形状分别为无限圆柱、球和无限平板(特征尺寸r=1m)的临界热爆炸温度Tacr、热感度概率密度函数S(T)；假定样品被气体包围，环境温度400K，温度波动幅度10K，由公式(20)～公式(21)计算样品1和样品2的安全度SD、热爆炸概率PTE。

(15)

(16)

(17)

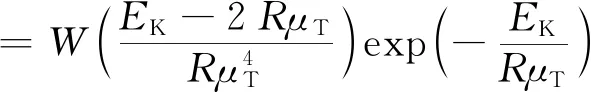
(18)

(19)

(20)

PTE=1-SD

(21)

式中：r为反应物特征尺寸(如平板厚度的一半，圆柱和球的半径)，m；δcr为热爆炸界限准数；-1为Lambert函数参量；λ为样品导热系数，W/(m·K)；ρ为样品密度，g/cm；EK、AK分别为Kissinger方程计算所得活化能和指前因子(见表2)；Q为样品反应热，样品1反应热为528.6J/g，样品2反应热为769.5J/g；σδ为Frank-Kamenetskii参数δ标准差；σT为实测环境温度T0的标准偏差；μT为Tacr的均值。

通过计算获得样品1和样品2在无限圆柱、球形和无限平板样品形状下的TS(T)max(S(T)对T曲线上的最大温度值)、Tacr、PTE和SD列于表6。

表6 样品1和样品2在不同形状下的TS(T)max、Tacr、PTE和SD

由表6可得，当样品形状为球形时，临界热爆炸环境温度和热安全度稍高，热爆炸概率较低，故球状样品相较于圆柱状样品和平板状样品的安全度最高。且样品1的临界热爆炸环境温度高于样品2，热爆炸概率低于样品2，说明NBR黏结剂体系ANPyO基PBX热安全性较高。

图3为样品1和样品2的热感度概率密度分布曲线。

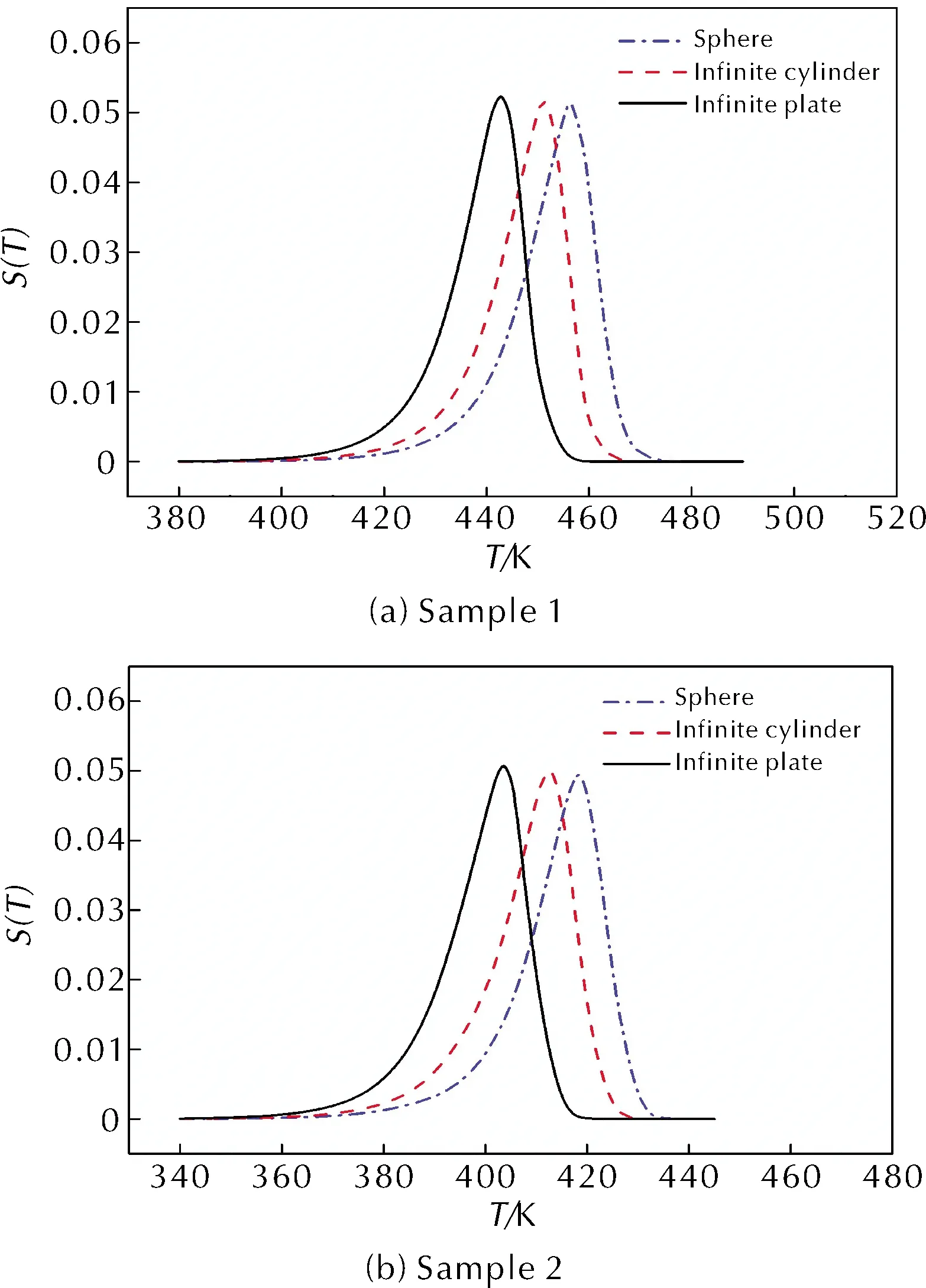
图3 样品1和样品2的S(T)—T关系曲线

由图3可见，S(T)—T关系在很大程度呈正态分布，相同实验条件下峰值温度TS(T)max, sphere>TS(T)max, infinite cylinder>TS(T)max, infinite plate，佐证了相同特征尺寸下球状样品比圆柱状样品安全，圆柱状样品比平板状样品安全。

3 结 论

(1)两种不同黏结剂体系的ANPyO基PBX热分解过程均由一个放热过程组成，利用热分解非等温热分解反应动力学研究，获得ANPyO基PBX热分解反应的表观活化能和指前因子，热分解的动力学机理函数积分式均为G(α)=[(1+α)1/3-1]2，微分式均为f(α)=3/2(1+α)2/3[(1+α)1/3-1]-1。

(2)丁晴橡胶NBR-26为黏结剂体系主体的ANPyO基PBX的活化能E=173.19kJ/mol，指前因子ln(A/s-1)=28.58；氟橡胶F2311为黏结剂体系主体的ANPyO基PBX的活化能E=143.78kJ/mol，指前因子ln(A/s-1)=22.89。

(3)丁晴橡胶NBR-26为黏结剂体系主体的ANPyO基PBX热安全性高于氟橡胶F2311为黏结剂体系主体的ANPyO基PBX。ANPyO基PBX形状为球形时，临界热爆炸环境温度和热安全度稍高，热爆炸概率较低，球状样品比圆柱状样品安全，圆柱状样品比平板状样品安全。