钢铁材料冲击疲劳行为综述

张遥辉

（南京航空航天大学航空学院飞行器设计专业，江苏 南京 210016）

1 概述

工程机械结构件在重复冲击载荷作用下，可能因损伤的累积引起裂纹萌生、扩展直至断裂，这样的过程称为冲击疲劳。有关结构在循环冲击载荷下疲劳行为的研究，目前尚未建立起完整的理论体系，而钢铁材料作为机械工程领域最常用的材料，研究其冲击疲劳失效行为以及寿命预测方法，对钢材的合理选择和制定相关的热处理工艺具有重要意义。

有关冲击疲劳的研究始于20世纪初。Standon等首先对九种不同成分的钢进行了连续冲击弯曲试验，研究了冲击破断次数与材料成分的关系，发现材料在大能量低周冲击下，破断能量与材料的冲击韧度有关；在小能量高周冲击下能量则大致正比于材料疲劳极限。McAdam随后也对几种钢材进行了循环冲击弯曲试验，验证了Standon的结论，提出了类似于常规疲劳极限的“冲击耐久性极限”的概念。Layland研究了循环冲击载荷下15种结构钢的疲劳失效行为，并绘制了每种材料的冲击能量A与寿命N的关系曲线。20世纪70～80年代，几位日本学者进行了大量试验，Iguchi测定了循环冲击下S20C钢的应力应变滞后环与应力波，讨论了缺口、应力比对σmax-N曲线的影响；Tanaka等自制冲击疲劳试验机，在室温及-50℃、-100℃低温条件下对低、中碳钢等材料进行了一系列冲击疲劳试验，获得了大量试验数据。在国内，周惠久等最先开展了冲击疲劳的研究工作，就材料化学成分、热处理、表面处理及试件的缺口效应、尺寸效应对冲击疲劳性能的影响进行了系统性探讨，取得了很多成果。

早期有关冲击疲劳的研究主要集中于总结材料在循环冲击载荷下的破断规律，寻找冲击疲劳与静疲劳的相关性，人们普遍认为，材料的冲击疲劳性能可以大致用静疲劳性能来表征。随着试验手段的进步，近年来，有关材料冲击疲劳的研究有了一些新进展。本文对当前国内外有关钢铁材料冲击疲劳行为的研究进行了综述，分析了疲劳过程中裂纹的萌生与扩展机制，讨论了影响材料冲击疲劳性能的主要因素，并总结了相关的冲击疲劳寿命估算模型，对今后冲击疲劳研究应当解决的问题进行了展望。

2 钢铁材料冲击疲劳失效行为

2．1 裂纹萌生与扩展行为

材料的疲劳失效过程由裂纹萌生与扩展两部分组成，其中裂纹萌生在总失效过程中占有很大比重，冲击疲劳也大致遵循相关规律。

郑修麟等观察了几种钢材在冲击疲劳下的裂纹萌生行为，发现在裂尖塑性区内，马氏体或贝氏体板条间的相对滑动量过大时将会通过应变积累形成微裂纹，随后相互连接并长大，形成了宏观裂纹。

王振明等研究了冲击疲劳下高锰钢裂纹萌生、扩展及断裂机理，发现试件缺口处晶粒在交变应力作用下产生了塑变诱发大量滑移线，与主应力轴约呈45°角，这些滑移线即成为裂纹源导致裂纹萌生。在随后的裂纹扩展阶段裂纹继续沿45°滑移线进行，途经各种缺陷时会向缺陷扩展，从而产生了方向改变及分支。

张萌观察了低碳钢在冲击疲劳循环形变阶段的微观特征，发现滑移是低碳钢在低周冲击疲劳载荷下循环变形的主要表现形式。滑移线往往贯穿着整个晶界或连续穿越晶界，随着疲劳周次的增加，滑移线从平直转向弯曲，产生了一种呈鱼脊状排列的滑移线窄带，如图1所示。

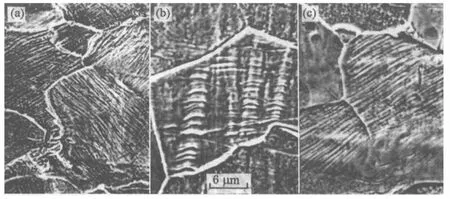
图1 10钢试件表面冲击疲劳滑移形貌

以上研究表明，材料在交变载荷作用损伤首先表现为微观的塑性形变，而滑移线是塑性形变在试件表面的可见特征，冲击载荷下的高应变速率会让材料中的形变过程表现得更加典型，冲击疲劳下材料的裂纹萌生行为与常规疲劳类似，且显微组织对于裂纹的萌生与扩展行为有着较大的影响。

2．2 与常规疲劳的对比

与一般疲劳载荷不同，循环冲击载荷下材料内部应力以波的形式高速传播，在遇到界面或截面尺寸改变时将发生反射、叠加等现象形成复杂的应力应变状态，对寿命产生重大影响。循环冲击载荷与一般的疲劳载荷相比，每次载荷作用有效时间很短，加载速率很高，材料的应力应变不均匀性要比非冲击疲劳载荷下大。

Iguchi观察了S20C钢光滑圆棒件与缺口板件的冲击疲劳和常规疲劳裂纹萌生过程，结果表明，光滑件的冲击疲劳裂纹萌生期高于常规疲劳，而有缺口时，则小于常规疲劳。由于光滑件在冲击疲劳下塑变滑移较常规疲劳困难，而材料塑变累积损伤是裂纹萌生的主要因素，因此，裂纹萌生在冲击疲劳下较难，体现为光滑试件的裂纹萌生期高于常规疲劳。在相同名义载荷下、冲击疲劳载荷下的试件缺口根部塑变区尺寸较常规疲劳下的小，因而冲击疲劳下的缺口敏感度较大，且由于冲击载荷导致材料的滑移变形更不均匀，集中在缺口根部某个微区内，导致缺口件在冲击疲劳下的裂纹萌生期小于常规疲劳。

于杰总结了冲击疲劳与常规疲劳下裂纹扩展的相关规律，在相同应力强度因子幅ΔK下，冲击疲劳与常规疲劳裂纹扩展速率与微观断裂机制的关系如表1所示。

当裂纹扩展形式皆为韧性断裂，材料屈服强度较高时，裂纹扩展遵循再生成核机制，即主裂纹前端区域由于塑变损伤累积产生许多微裂纹，在随后的循环应力作用下微裂纹不断长大，最后，与主裂纹连接而导致宏观裂纹。因相同条件下常规疲劳的裂尖塑变程度及区域都比冲击疲劳下的大，所以，材料在冲击疲劳下的裂纹扩展速率比常规疲劳低。

当材料屈服强度较低时，在韧性断裂条件下，裂尖塑变在两种疲劳载荷下都易进行，裂尖塑变区都较大，裂纹扩展遵循裂尖钝化-复锐机制。两种疲劳载荷下裂纹扩展过程中，裂尖均能通过塑性滑移充分钝化，因此，裂纹扩展速率基本相同。

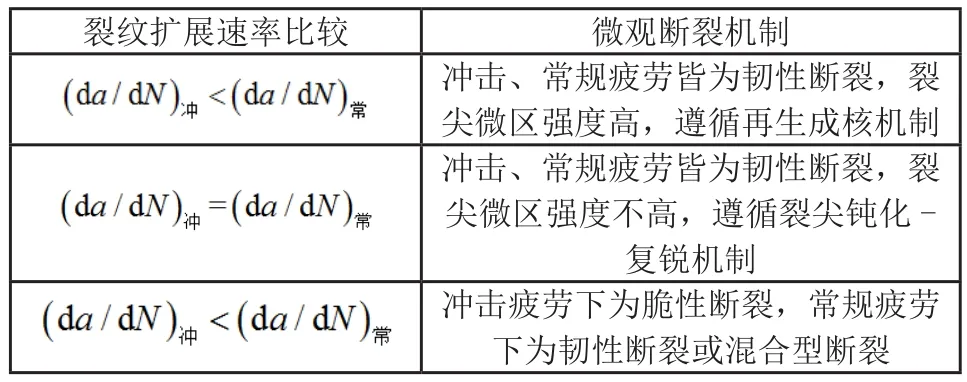
表1 裂纹扩展速率与微观断裂机制的关系

当材料在冲击疲劳下为脆性断裂(沿晶、解理)，而在常规疲劳下为韧性断裂或混合型(脆性+韧性断裂)时，冲击疲劳的裂纹扩展速率高于常规疲劳。这是因为，脆性断裂下裂纹扩展所消耗能量远小于韧性断裂，且裂纹扩展阻力小于韧性断裂的缘故。

3 影响钢铁材料冲击疲劳性能的因素

通常，影响材料静疲劳性能的因素也会影响其冲击疲劳性能，但影响的程度有所差别，以下将分别介绍载荷特性、环境温度、热处理方式等因素对钢铁材料冲击疲劳性能的影响。

3．1 载荷特性

载荷对钢铁材料冲击疲劳寿命的影响，主要表现在载荷大小以及加载方式。

北浦坚一研究了平均应力对低碳钢冲击疲劳强度的影响，对SS41钢光滑与和缺口件在不同应力比下进行冲击疲劳和常规疲劳试验，其中缺口件的应力幅值-寿命结果如图2所示。

结果表明，冲击疲劳与常规疲劳的应力幅值-寿命曲线在双对数坐标图上均呈现出较好的线性关系，冲击疲劳寿命在改变应力比的情况下的变化得比常规疲劳更为明显，尤其是在应力幅值较高时。

张镇生等对40Cr和20CrMnTi钢圆棒件进行冲击弯曲疲劳试验，分别采用了三点弯曲和四点弯曲冲击的加载方式，测定的试验结果如图3所示，四点弯曲加载条件下材料的疲劳寿命显著高于三点弯曲加载，且当两种加载方式下试件的最大应力接近时，试件的疲劳寿命也近似一致。

以上研究表明，冲击疲劳下材料的寿命较常规疲劳显著下降，且相同能量下四点弯曲加载的寿命显著高于三点弯曲。

3．2 缺口效应

冲击载荷的特性导致能量的消耗主要集中在构件的薄弱环节，因此，缺口的存在会导致构件的冲击疲劳寿命大大下降，构件在冲击疲劳载荷下的缺口敏感度更大，承受冲击载荷的零构件设计若采用非冲击疲劳的缺口应力集中系数为依据，可能会导致零构件过早失效。

文献对不同缺口尺寸的40钢试件进行了冲击疲劳试验，结果如图4所示。

可以看出，在试件带缺口的情况下冲击疲劳寿命将显著下降。对材料在不同应力集中系数Kt下的冲击疲劳性能的研究表明：在无缺口或钝缺口情况下，冲击疲劳强度对材料的塑性要求较低，而在尖缺口乃至裂纹的高应力集中情况下要求较高。

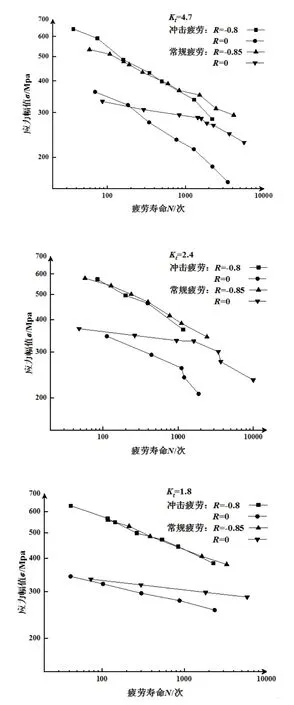
图2 SS41钢缺口件冲击疲劳与常规疲劳应力幅值-寿命曲线

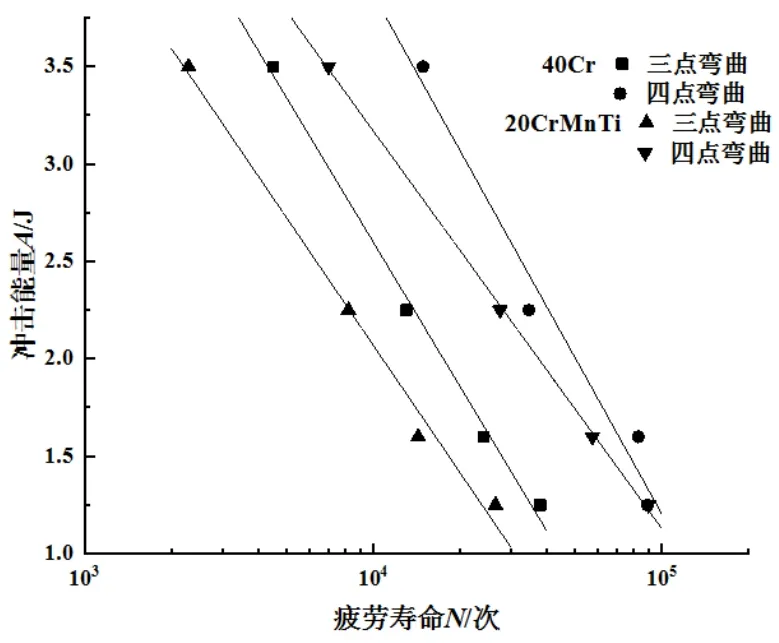
图3 40Cr与20CrMnTi两种加载方式下冲击能量与寿命曲线

图4 40钢试件不同缺口尺寸下的冲击疲劳寿命

胡光立等进行了300M钢缺口件的冲击疲劳试验，结果表明，应力集中程度的增加会导致试件寿命急剧下降，且与常规疲劳相比，下降趋势会更加明显，体现出冲击疲劳更敏感的缺口效应。

综合以上研究，我们对冲击疲劳下材料更加敏感的缺口效应引起重视，工程应用中承受冲击的结构件应尽可能地避免缺口存在。

3．3 环境温度

有关环境温度对钢铁材料冲击疲劳性能的影响，也有学者展开了研究。Yarema等对30CrMnSiNiA钢在室温以及-120℃下的冲击疲劳性能进行了试验对比，发现钢的整体耐久性随温度降低而提高，且随着温度的降低裂纹萌生的时间增加，但裂纹扩展的时间减少。Akizono等对一种Cr-Mo合金钢进行冲击疲劳试验，发现从室温降低到-150℃过程中，沿晶开裂和解理开裂的失效形式越来越普遍，裂纹扩展速率加快。Matsumure等研究了碳含量分别为0.39%和0.63%的普通碳钢在室温和-30℃下的冲击疲劳性能，两种钢在室温下的冲击疲劳寿命均比常规疲劳短，裂纹扩展速率也更高。含碳量较低的钢在-30℃时发生解理，但在室温下没有；含碳量较高的钢在两种温度下都能观察到解理现象。冲击疲劳试件断口下，塑性区深度仅为常规疲劳的1/3左右。

3．4 热处理方式

目前，有关热处理方式对钢铁材料冲击疲劳性能影响的研究，主要集中在淬火和回火温度上。

刘福祥等研究了热处理工艺对W6Mo5Cr4V工具钢冲击疲劳性能的影响规律，采用了Ф10mm×100mm的光滑试件，分别在不同淬火温度和回火温度下进行试验。材料的寿命与淬火温度及回火温度的变化规律如图5所示。

结果显示，三种能量下疲劳寿命都随淬火温度的升高而降低，且低能量的寿命变化幅度大于高能量。淬火温度的升高会减弱材料的微区塑性变形能力，降低材料的冲击疲劳性能，由于微区塑变引起的应力松驰效应对不同冲击能量的缓解作用不同，对低能量的缓解作用必然要大于高能量，即对寿命的影响随能量的增大而减小，使得低能量下的疲劳寿命的变化幅度大于高能量。

右图三种能量下疲劳寿命的峰值均出现在500～560℃段内，该回火温度恰好是W6Mo5Cr4V2钢的二次硬化温度。随着回火温度的升高，内应力减小且碳化物弥散析出增多，弥散强化作用增强，能够阻止微裂纹的扩展，增强材料冲击疲劳性能，在二次硬化时达到峰值，此后，再提高回火温度会因碳化物的聚集降低疲劳性能。

图5 冲击疲劳寿命与淬火、回火温度的关系

Yarema等在研究30CrMnSiNiA钢不同回火温度下冲击疲劳性能时发现，回火温度在250℃时可获得最大的冲击疲劳寿命，此时，裂纹萌生寿命与抗拉强度也会处于最佳状态。Molchanov等也在对几种Cr-Ni钢的研究中发现，在220～240℃范围内回火时材料的冲击疲劳性能要比在180～200℃范围内更好，这一结果与Yarema的结论相符。

在含大量合金元素的淬火合金钢上形成的残余奥氏体对材料冲击性能有一定的影响。Kozyrev等对一种含11.5%Cr的工具钢进行冲击疲劳试验，发现在高应力水平下，残余奥氏体可提高该工具钢的冲击疲劳性能，但在低应力水平下，则相反。Pestov等通过热循环在马氏体时效钢中生成残余奥氏体，提高了低周冲击疲劳性能，这是裂尖的奥氏体转变为铁素体产生了应力松弛导致的。

以上研究表明，热处理方式会对钢铁材料的冲击疲劳性能产生较大影响，针对不同成分的钢材，需要通过试验以获得最佳性能。

4 钢铁材料冲击疲劳寿命估算方法

当前，有关冲击疲劳的寿命分析方法还没有完善的理论框架，国内外针对循环冲击载荷下的材料的损伤累积与失效规律的研究，采用的方法主要有能量法与应力法，随着损伤力学与有限元技术的发展，一些新的方法也被应用于冲击疲劳寿命估算中。

4．1 能量法

能量法通过测定冲击能量A与材料破断循环数N之间的关系曲线（即A-N曲线）来评定材料的冲击疲劳性能，从而为寿命估算提供参考。图6为A-N曲线的示意图，其中A0为冲击疲劳极限能量，Ak为一次冲击下材料即破坏的能量值，且Ak=ak·F，其中ak为材料的冲击韧性，F为破坏位置横截面积。

图6 材料的A-N曲线示意图

针对冲击疲劳试验尚未标准化的现状，许多研究者为了能将冲击疲劳问题进行定量化研究，对材料的A-N曲线采用了经验公式拟合。A.A.Johnson等基于Standon和Bairstow的试验数据，对八种不同成分的珠光体钢的冲击疲劳寿命进行了统计，发现当寿命Nf在1000～50000次时，与冲击能量A可以拟合为以下形式的三参数经验公式：

其中，A0可代表冲击疲劳极限，Ai为冲击疲劳参数，p为冲击疲劳指数，其值可取为0.6。在大能量低周冲击的情况下，冲击能量与寿命又可拟合为：

其中，q为低周冲击疲劳指数，与钢材中碳含量有关，系数m与q存在关系：

其中C与D为常数，通过拟合试验数据分别为0.128与0.075，联立式（2）、（3）可得：

采用能量表征冲击疲劳寿命的方法虽然直观，但却有很大的局限性，对于某一特定材料的试件，在某一冲击循环次数下断裂的能量大小与试件几何因素及载荷情况等试验条件有关，以A-N曲线表征材料冲击疲劳性能，只能作为一种条件性的相对比较，曲线中的冲击疲劳极限，也无法直接作为材料的疲劳性能指标，所以其结果无法直接应用于机械产品零件的设计和强度分析的定量计算。

4．2 应力法

应力法以结构在冲击载荷下的峰值应力σmax与破断循环数N之间的关系曲线（即σ-N曲线）来表征，将循环冲击载荷作用下的研究成果与规律用于结构强度的分析与设计，便于与一般载荷下的疲劳损伤强度理论相比较，借以充实冲击疲劳损伤的强度设计方法。

文献的试验数据表明，针对缺口试件，当冲击疲劳试验结果用缺口危险点处塑变范围Δεp与循环寿命N表示时，二者间的关系符合Manson-Coffin定律：

其中，εf是疲劳延性系数，c为疲劳延性指数。基于这个规律，邹远鹏等采用局部应力应变法对结构冲击疲劳寿命进行估算。假定试件缺口根部作为疲劳裂纹的起始，且由假想单轴疲劳元的断裂所引起，如图7所示，若疲劳元具有与光滑试件相同的应力应变历程，则光滑试件的疲劳寿命可认为与缺口试件一致。

图7 冲击弯曲疲劳试件缺口根部塑性区及假想单轴疲劳元示意图

由此导出的寿命估算表达式为：

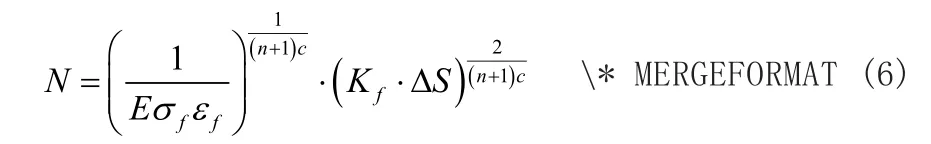
式中，ΔS为试件所受的名义应力幅，Kf为疲劳缺口系数，n为形变硬化指数，σf为疲劳强度系数。

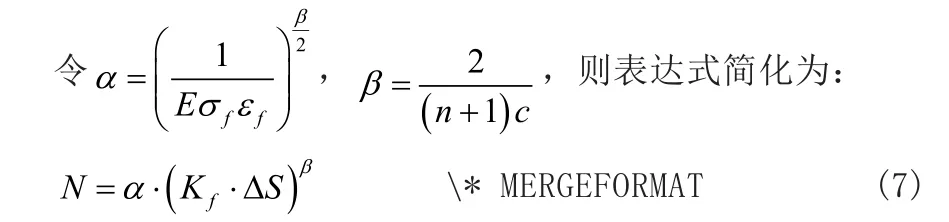
由于该式并未考虑冲击能量对试件应变速率的影响，需要引入一补偿因子v：

A为冲击能量，A0为试验的最小能量，则考虑应变速率影响后的寿命估算表达式为：

对于40CrNiMoSi钢缺口件，估算寿命曲线与试验结果如图8所示，取得了较好的预测结果。

图8 40CrNiMoSi钢缺口件估算寿命与试验结果

4．3 损伤力学法

Lemaitre等建立的损伤力学方法通过引入损伤度的宏观概念来表征材料力学性能在疲劳载荷作用下的劣化过程，为研究疲劳裂纹的萌生提供了新途径。损伤力学理论认为，材料在循环载荷作用时，其应力应变场与损伤场耦合使得损伤场不断随载荷循环而发生演化，结合损伤力学理论与有限元方法来分析损伤场与应力应变场的耦合作用，对于工程实际有着很大的应用价值。Lemaitre基于连续介质热力学导出的三维各向同性塑性损伤演化方程为：

其中，S与c为材料参数，Y为损伤应变能释放率，p为累积塑性应变率，且

式中，σeq为等效应力，Rv为应力三轴度，σm为静水应力，v为材料泊松比。

基于上述理论，文献[27]根据超低周冲击疲劳试验结果，提出了多轴应力状态下的超高周冲击疲劳寿命预测的平均损伤模型：

该模型在Lemaitre损伤演化方程的基础上引入了一个指数项b，对冲击疲劳过程中非均匀的累积塑性应变率进行了平均，从而可以只使用第一次冲击的塑性应变数据进行寿命估算。式中的参数S、c、b、K可以通过冲击疲劳试验的寿命数据进行拟合得到，σeq与则可由有限元仿真计算得到。此法对AerMet100钢缺口件冲击疲劳寿命的预测结果如表2所示。

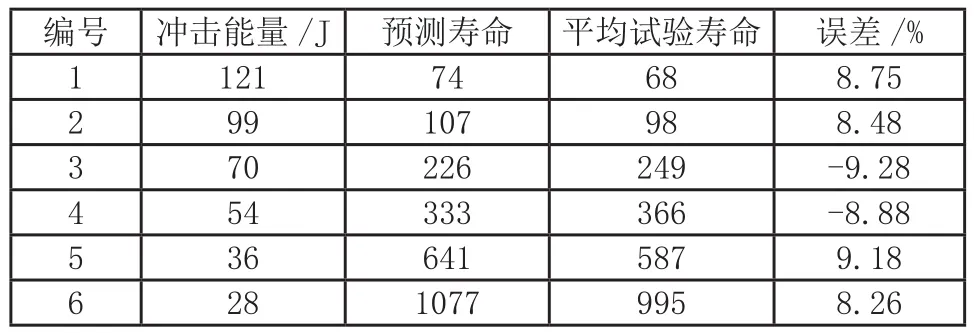
表2 不同冲击能量下预测寿命与试验数据的比较

从预测结果看，该模型能够较好地预测构件的超低周冲击疲劳寿命。

4．4 总结

以能量法对材料的冲击疲劳寿命进行估算，一般是基于试验结果采用唯象经验公式对A-N曲线进行拟合，而应力法主要关心材料在冲击载荷下应力应变响应的峰值状态，主要基于疲劳危险点处的局部应力应变对结构的寿命进行分析。从应用前景上看，应力法可适用于不同的构件外形，而能量法则缺乏理论基础，需要大量的试验数据，且仅适用特定外形的结构。基于损伤力学理论发展的冲击疲劳寿命估算方法则充分考虑了材料在循环载荷下的性能劣化过程，借助不断完善的有限元技术，为结构在循环冲击载荷下的寿命分析提供了新的手段。

5 结论与展望

冲击疲劳是工程领域中不可忽视的一种结构失效形式，在经济社会不断发展的背景下，众多机械零部件的设计面临着越来越高的性能需求，认识材料在循环冲击载荷下的失效和断裂机理，掌握各种条件下材料冲击疲劳行为的规律，有利于提出改善材料冲击疲劳性能的措施，对于使用范围广泛、品种繁多的钢铁材料而言，更值得去开展相关的研究。

钢铁材料在冲击疲劳载荷下的失效行为，与常规疲劳有一定的相似性，但也有一些新的特点，如应力应变响应状态更加复杂、对缺口的敏感度更大、在大载荷下更易发生脆性断裂等等。目前，尽管许多学者对于各种钢铁材料的冲击疲劳行为已有不少研究，但是，大多依然停留在试验层面，还尚未能构建出能够广泛应用的损伤累积理论与寿命估算模型。由于尚未有相关的冲击疲劳试验标准，研究者往往只能自行设计试验，在试验条件各不相同的情况下，这些试验数据相互之间难以进行分析比较，因此，对于冲击疲劳的研究尚处于初级阶段。随着计算机技术的发展以及有限元分析软件的完善，结构在冲击载荷下的响应分析的手段越来越丰富，借助于仿真模拟结构在冲击下的响应历程，为构建理论模型提供依据，这是冲击疲劳研究的一个方向。