基于蒙特卡洛模拟法的动车组裙板装配优化研究

王锋

（中车长春轨道客车股份有限公司，吉林 长春 130000）

动车组在高速运行时铁轨附近的杂物极易撞击到车下部件，因此，裙板和底板对于降低空气阻力和保护车下设备具有重要意义。然而，头车转向架裙板作为整车装配工艺中最后的工序环节，经常因为制造和装配的误差累积，导致裙板或裙板间隙处防寒胶条无法装配。为解决装配干涉问题，往往采用现场研配、磨削裙板吊耳等方法，这增加了人力和工时成本，延误了车辆交付时间。影响头车转向架裙板装配的因素繁多，难以从单一环节控制装配尺寸，这就对裙板尺寸链设计提出了严格的要求。

转向架作为列车动力输出、制动安全的关键，需要裙板提供安全保障，因此，裙板装配尺寸链在动车组设计过程中，是重点计算的项目之一。本文结合蒙特卡洛模拟法，研究裙板尺寸链设计优化方法，减少干涉现象。

1 蒙特卡洛法的原理与应用

1．1 蒙特卡洛模拟法的原理

蒙特卡洛法(Monte Carlo)是统计试验计算方法，高斯正太分布的期望值µ决定函数分布位置，标准差σ决定函数分布幅度，其概率密度函数公式如下：

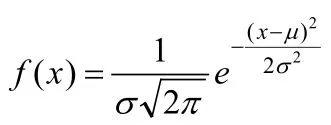
根据中心极限定理，当统计样本足够充足时，各独立同分布随机变量之和的分布趋近于高斯正态分布，且尺寸分布符合伯努利大数定律。因此，蒙特卡洛模拟法计算中所求数学期望即可通过函数f(x)的积分获取。

1．2 蒙特卡洛模拟法的模型建立与应用

在实际工程应用中，每件产品的生产和加工均可进行独立随机抽样，其尺寸和公差作为尺寸链的封闭环或组成环可作为模型建立的参数。当第i个封闭环或组成环为Ai，所求环为Ax，模拟次数为n时，则所求封闭环或组成环尺寸满足如下公式：

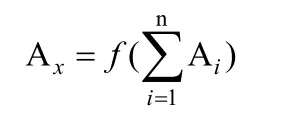
模型函数通过尺寸链几何关系确定后，即可将未知尺寸转化为随机变量的统计学问题进行分析，得到所求尺寸和公差，通过模拟计算，可知其数学期望和标准差如下：

（1）数学期望

（2）标准差

2 基于蒙特卡洛模拟法的裙板尺寸链计算

2．1 蒙特卡洛模拟法的计算逻辑

针对模型中随机变量的高斯正太分布规律和标准差等数学特征参数进行计算，随机模拟实验的基础是充足的模拟数据，因此，需要根据精度要求设定置信区间，输入对应的置信度作为循环终止条件。

2．2 动车组裙板尺寸链分析

转向架处的裙板组在单侧共包括四块玻璃钢单块裙板，每块外形的弧度和长度都存在较大差异。1号裙板与前端配合时，两者端面的平面平行度有着严格要求，而2号和4号裙板弧面较大，成型后加工难度较大，所以将结构相对简单的3号裙板作为优化目标。3号裙板为封闭环A，1号、2号和4号裙板分别为减环A2、A3和A4，整体预留空间尺寸A1为增环，每块防寒胶条e（5mm）不具有公差。明确各组成环几何关系和公差范围后可以得到尺寸链方程为A=A1-A2-A3-A4-3e ，各组成环尺寸和换算后的对称偏差尺寸如表1所示，使用极值法计算出封闭环均值A=1809.3mm，极大值Amax=1813.3mm，极小值Amin=1805.3mm。

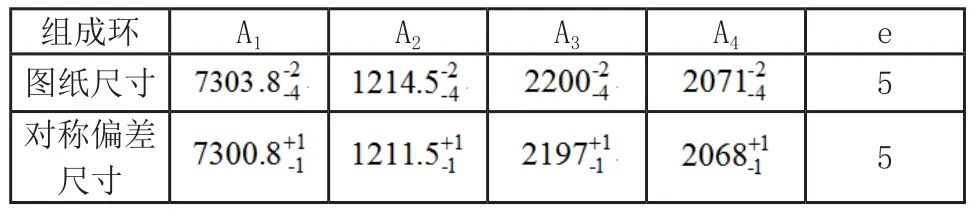
表1 尺寸链组成环尺寸及公差（单位：mm）

2．3 MATLAB 模拟计算

调用函数normrnd生成封闭环随机数值，当模拟矩阵阶次为N时，可以得到[N,N]矩阵的子样，样本中共包含N2个数据，代入尺寸链方程计算封闭环尺寸的数学期望、标准差和极值，预设模拟计算的置信水平为99.7%，模拟函数如下：

A1=normrnd(7300.8,1/3,[N,N]); %%生成组成环

A2=normrnd(1211.5,1/3,[N,N]); %%生成组成环

A3=normrnd(2197.0,1/3,[N,N]); %%生成组成环

A4=normrnd(2068.0,1/3,[N,N]); %%生成组成环

A=A1-A2-A3-A4-15; %%生成封闭环

mean(mean(A)); %%计算封闭环矩阵的数学期望

std2(A); %%计算封闭环矩阵的标准差

当模拟矩阵阶次N=1000时，正态分布曲线如图1所示，其数据分布于置信区间内。

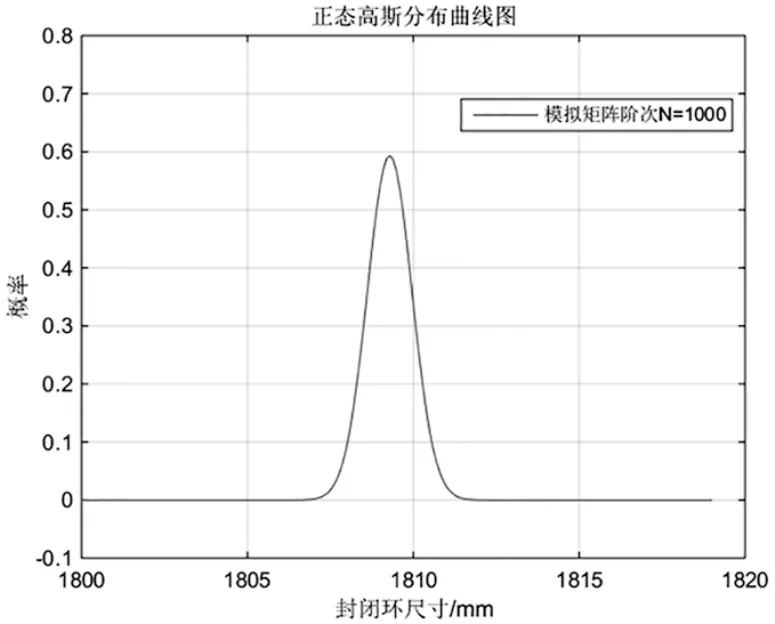
图1 高斯正态分布曲线

如图2所示，当模拟矩阵阶次N变化时，其数学期望也在不断变化，且随着模拟次数的增加，计算样本规模也在扩大，其变化波动逐渐降低，在预设置信水平的前提下，当MATLAB中模拟矩阵阶次N足够大时，封闭环的数学期望与标准差逐渐无限趋近于某稳定值，即可作为生产的理论值。

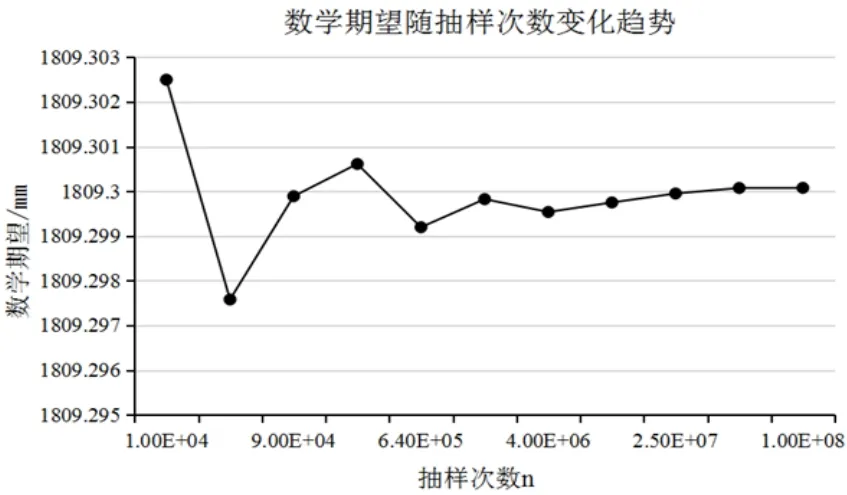
图2 数学期望随抽样次数变化趋势

3 结语

本文讨论了蒙特卡洛模拟法的基本原理和工程应用方法，并针对动车组头车转向架玻璃钢裙板尺寸链进行了模拟计算，通过优化分析，在与实际生产情况高度拟合的前提下，得到较高的计算精度。