基于马尔科夫随机场的SAR图像超像素分割算法

宋文青 董 锦 相 飞 张 俊

(西安电子工程研究所 西安 710100)

0 引言

合成孔径雷达，具有全天时、全天候的工作特点，在目标检测、海陆分割和森林测绘等领域具有广泛的应用[1]。近年来，随着SAR系统分辨率的不断提升，对于相同的观测场景，SAR系统能够获取的图像像素成倍数增加。SAR图像分辨率的提升，一方面为观测场景提供了更加丰富的纹理信息；而另一方面也为图像解译算法增加了信息输入维度，进而大大提高算法的计算复杂度。

图像超像素，是指由图像中具有某种相似特征的局部相邻像素聚类而形成的同质区域[2]。与图像的像素表征形式相比较，超像素表征能够有效减少图像中的冗余信息，降低后续处理算法的复杂度。同时，基于超像素能够提取出更为丰富的描述性特征，进而提高后续处理算法的鲁棒性。基于以上优势，图像的超像素分割近来得到国内外学者的广泛研究，并取得了大量优秀的研究成果[3-8]。纵观已有的图像超像素分割方法，可以将其分为基于图割技术的超像素生成方法和基于聚类技术的超像素生成方法两大类。基于图割技术的超像素分割代表方法有标准化切割(Normalized cut, N-cut)算法[3]和Felzenszwalb和Huttenlocher提出的图割[4]算法等；基于聚类技术的超像素分割代表方法有快速移位(Quick-Shift,QS)算法[5]和简单线性迭代聚类(Simple Linear Iterative Clustering, SLIC)[6]算法等。SLIC算法[6]在像素的[L,A,B,X,Y]特征空间采用局部K-means聚类技术进行图像的超像素提取。算法具有计算速度快、分割精度高和应用便捷的优势，在光学图像处理领域得到广泛应用。不同于光学图像的高斯加性噪声假设，SAR图像中存在大量的乘性相干斑噪声，这就导致由光学图像应用背景下提出的超像素分割方法不能直接应用于SAR图像处理中。以SAR图像散射统计特性出发，通过修正SLIC算法中的相似性距离公式，学者们提出了众多适用于SAR图像超像素分割的改进型SLIC算法[9-12]，进而提高算法分割的性能。SLIC类超像素分割算法中没有对超像素分割区域的连通性进行约束，分割结果中会出现部分不连通的超像素区域，因此需要进一步的后续处理[6]。对于SAR图像，由于相干斑噪声的影响，分割结果中这种不连通现象变的非常严重，且超像素边界不光滑。这种不连通现象可以通过增大超像素的紧致性约束得到一定程度的抑制，但同时也会导致超像素图像边界的贴合性能降低。在SAR图像分割领域，为了能够有效抑制相干斑噪声的影响，通常采用基于马尔科夫随机场模型的分割方法，利用图像上下文相邻像素的关联性约束从而提高分割区域的空间连通性以及边缘的光滑性[13-15]。基于此，本文进行SAR图像超像素提取时，一方面考虑到超像素内部像素的特征一致性约束和超像素形状的紧致性约束，另一方面又引入了图像上下文相邻像素的马尔科夫关联性约束，以保证生成的超像素具有均匀同质、结构紧致和空间平滑的特点。

文章内容安排如下：第1节中，在贝叶斯统计理论框架下给出本文基于马尔科夫随机场分割算法的最大后验概率优化模型；第2节中，给出模型的局部迭代条件优化求解过程；第3节中，对本文超像素分割方法的分割性能进行分析验证；第4节中，对本文算法进行总结。

1 基于MRF的SAR图像超像素分割模型

在贝叶斯框架下，本文基于马尔科夫随机场的SAR图像超像素分割方法可以表示成如式(1)所示最大后验(Maximum A Posteriori, MAP)准则优化目标函数[16]

(1)

(2)

在图像超像素分割应用中，通常利用像素的灰度(或颜色)特征进行散射均匀性约束，并利用像素的坐标特征进行形状紧致性约束[6]。因此，为了生成散射均匀且形状紧致的超像素，式(2)中的像素特征随机变量F同样采用图像像素灰度特征Z和坐标特征[X,Y]，即F=[Z,X,Y]。假定图像像素灰度变量Z和其坐标变量[X,Y]满足独立同分布，式(2)可以进一步转换为

(3)

式(3)中，等式右侧三项分别为超像素的均匀同质约束项、紧致性约束项和分割标号的空间上下文关联性约束项(即马尔科夫特性约束项)。

1.1 均匀约束

SAR图像像素取散射强度特征时，其服从Gamma分布[1]。假定各像素之间满足独立分布特性，给定超像素分割S=s，似然概率p(Z=z|S=s)可以表示为[1]

(4)

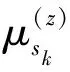
(5)

其中，Nl为超像素l所包含的像素个数。

1.2 紧致约束

超像素的紧致性是对超像素内部像素在空间上分布的描述，一般采用二维高斯分布进行度量[6]。给定超像素分割S=s，似然概率p(X=x,Y=y|S=s)可以表示为

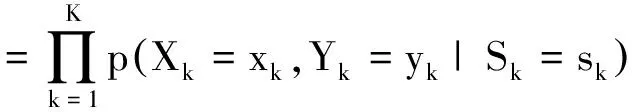
(6)

(7)

1.3 平滑约束

超像素平滑性约束要求超像素分割区域在空间上具有连通特性和边缘具有光滑特性。本文通过利用MRF模型对超像素分割标号随机场进行统计建模以实现超像素分割的平滑处理。记={Nk|k∈[1,2,…,K]}为定义在网格Ω上的邻域系统，其中Nk为像素k的邻域像素集合[16]。假设S为邻域系统上的马尔科夫随机场，则其概率分布具有正定性和马尔科夫性[16]，如式(8)所示。

(8)

其中，{1，2，…，K}-{k}表示除像素k外其他像素集合，定义c为邻域系统上的一个基团[16]，则其内部所有元素都是两两相邻的，即当i,j∈c时，i∈Nj且j∈Ni，i≠j。根据Hammers-Clifford定理可知[16]，当随机场S服从MRF分布时，其联合概率分布函数等价于Gibbs分布，如式(9)所示。

(9)

式(9)中，Z为归一化因子，T为温度变量，Vc(s)为基团c势能，为所有基团的集合。对于图像分割问题，联合概率分布通常仅采用二阶成对基团的势能进行建模，而其他非成对基团势能置为0[15-16]，则公式(9)可简化为

(10)

其中，二阶势能函数表达式为

(11)

将式(4)、(6)和(10)代入式(3)，并化简，可得以下超像素分割优化模型

αEc(z,x,y,s)+βEs(z,x,y,s)]}

(12)

其中，

α=S2/2σ2

β=1/T

(13)

式(12)和(13)中，E(z,x,y,s)为关于图像分割结果的总势能函数，Eh、Ec和Es分别为超像素均匀项、紧致项和平滑项的势能函数；S2为超像素期望尺寸；α和β分别为紧致和平滑约束因子。α越大，超像素形状越趋紧致；β越大，超像素分割结果越光滑。

2 局部迭代条件模型优化算法

(14)

其中，E(zk,xk,yk,sk)为像素k的势能；∑E(zj,xj,yj,sj)为除像素k外其他像素的势能和，Φk为像素k的标号搜索空间。

本文ICM迭代算法处理流程如表1所示。

表1 本文ICM迭代算法处理流程

步骤处理内容步骤1:给定超像素期望大小S,按照均匀网格划分生成初始超像素分割结果素分割s=s(0),如图1所示;设置最大迭代次数Iter,及初始迭代次数iter=0;步骤2:根据当前分割结果s=s(iter),利用式(5)和式(7)对各超像素的统计模型参数μ^zl、μ^xl和μ^yl进行最大似然估计;步骤3:遍历图像像素k=1,2,…,K,利用式(14)对各像素标号进行更新s=siter+1();步骤4:iter=iter+1,判断是否满足终止条件,如果不满足则重复步骤2;如果满足则输出分割结果s。

同时，为了提升算法的计算效率，迭代过程中将像素标号的搜索空间限定于图像的局部区域内。图1中给出了像素k标号搜索空间Φk的确定示意图。其中，k点为当前待更新像素k，虚线区域为其邻域范围，仅当超像素的坐标中心落入该区域内时，其对应的标号才进入像素k的标号搜索空间Φk。图1中给出了落入该像素邻域范围内的4个超像素中心，即Φk={l1,l2,l3,l4}。可以看出，Φk相对整个标号空间，数量大大减小，从而使迭代算法的计算复杂度大幅降低。

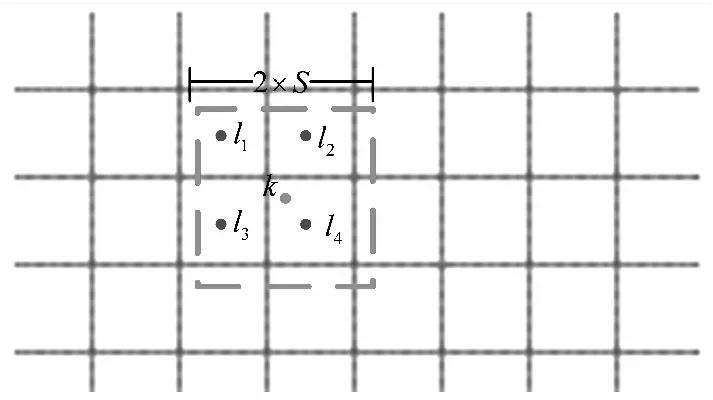
图1 初始超像素分割示意图

由于算法并没对超像素区域的连通性进行强约束，分割结果s中依然会存在少量的不连通分割区域。因此，算法最后需要对这些孤立的像素点或小区域与其相邻超像素进行合并，得到最终的超像素分割结果。

3 实验结果与分析

本节中，采用仿真SAR图像数据对本文基于MRF的超像素分割算法与文献[9]中SLIC类超像素分割算法进行对比，两种方法分别简称为SAR-MRF和SAR-SLIC方法。SAR-MRF算法中，紧致因子α和光滑因子β分别设为1和1；SAR-SLIC算法中权值设为3(依照文献[9]设定)；两种方法迭代次数统一设为5，期望超像素大小S设为20。图2中给出了两个不同场景、不同视数SAR仿真图像及不同方法的超像素分割结果。

图2中，图a1和图b1分别为场景1在视数为1和4时的仿真SAR图像；图c1和图d1分别为场景2在视数为1和4时的仿真SAR图像。可以看出，图像的视数N越低，其相干噪声越严重。图a2、b2、c2和d2分别为四幅仿真SAR图像的SAR-SLIC超像素分割结果，图a3、b3、c3和d3分别为四幅仿真SAR图像的SAR-MRF超像素分割结果。从实验结果可以看出，由于本文SAR-MRF算法中引入了标号场的马尔科夫性约束，其图像边界处抗噪能够更强，分割结果中超像素边缘贴合性更好，且边缘更为光滑。特别是对于视数为1的SAR图像，该优势更为明显。

进一步，本节采用边界召回率(Boundary Recall, BR)、欠分割错误率(Undersegmentation Error, UE)和可达分割精度(Achievable Segmentation Accuracy, ASA)三个性能指标对超像素分割结果进行定量评估。其中，边界召回率描述了超像素边界与真实边界的贴合程度，欠分割错误率描述了图像真实分割区域被超像素欠分割的面积的比例，可达分割精度描述了以超像素作为最小处理单元时图像分割能够达到最大分割精度。可以看出，边界召回率越小、欠分割率越低和可达分割精度越高，则超像素分割算法的分割精度越高。

图3中分别给出了视数为1和4时的仿真SAR图像两种方法分割结果各性能指标曲线，横坐标表示超像素的大小。图3实验中同样采用图2实验观测场景。对于相同视数的两个场景，分别进行10次SAR图像仿真，然后统计平均在不同期望超像素大小情况下超像素分割结果的各性能指标。

从图3实验中可以看出，两种方法的分割精度与超像素大小成反比关系，即期望超像素尺寸越小，超像素分割精度越高，符合超像素分割的特点[6]。同时也可以看出，与SAR-SLIC算法相比较，本文SAR-MRF算法在不同超像素大小和不同视数情况下其分割精度都相对更高。特别是对于相干斑噪声严重的视数为1的SAR图像，SAR-MRF算法优势更为明显，与图2实验结果分析相吻合。

4 结束语

针对SAR图像超像素分割问题，本文提出一种基于马尔科夫随机场的超像素分割方法。算法中融合了超像素相似性约束、紧致性约束和马尔科夫特性约束，使提取的图像超像素具有散射均匀、形状规则和边缘光滑的特点。实验结果表明，相对于传统SAR图像超像素分割方法，该SAR-MRF算法的相干斑噪声抑制能力更强，分割精度更高。

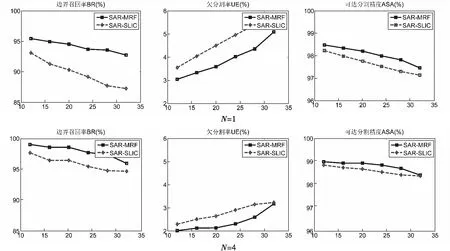
图3 SAR-MRF和SAR-SLIC分割结果性能指标对比