2020年高考理科数学模拟试题
2020-05-11许少华
许少华
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
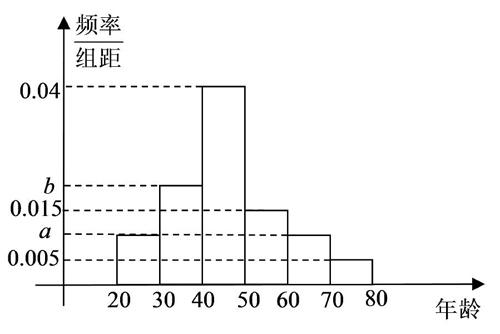
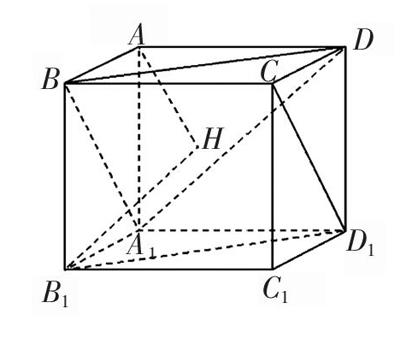
1. 设集合A= {x│-2 A. (0, 2) B. (-2, 4) C. (-2, 0)∪(2, 4) D. (-2, 0]∪[2, 4) 2. 已知复数z1=2+i, z1·z2 =2-i,则复数z2的共轭复数为 () A. ■+■i B. -■-■i C. ■-■i D. -■+■i 3. 设f(x)为定义在R上的奇函数,当x≤0时,f(x)=2x+log2(x2+1)+a (a为常数),则f(1)=() A. ■B. 1C. -1D. -■ 4. 据统计中国人民政治协商会议第十二届全国委员会到会委员有1500名,从中抽取150名对他们的年龄进行统计,其频率分布直方图如图,其中年龄在[30,40)的委员人数为30人,则估计年龄在[60,80)之间的委员人数为() A. 150 B. 200 C. 225 D. 250 5. 已知雙曲线C ∶ ■-■=1(a>0,b>0)的焦距为2c,焦点到双曲线的渐近线的距离为■,则双曲线C的离心率为() A. 2 B. 3 C. ■ D. ■ 6. 若?琢为锐角,且cos(+■)=■,则sin(+■)=() A. ■B. ■C. ■D. ■ 7. 如图所示,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H,则以下命题中,错误的命题是() A. 点H是△A1BD的垂心 B. AH垂直于平面CB1D1 C. AH的延长线经过点C1 D. 直线AH和BB1所成角为45° 8. 若△ABC的三边长a,b,c满足a=4sinB,sin2AsinC=■且,则△ABC的面积为() A. ■ B. ■ C. 25 D. 24 9. 如图,ABCD为等腰梯形,若CD=■AB=4,且梯形面积为20,当E为BC中点,F,G分别为DA的三等分点时,■·■ 的值为 () A. -■B. -■ C. -■D. -■ 10. 已知函数f(x)=Asin(x+)(A>0,>0,<■), 在一个周期内的图像如右图所示,函数f(x)的图像向右平移■后得到g(x)的图像,则g(x)的一个单调区间为 () A. (0,■) B. (■,■) C. (-■,■)D.(-■,■) 11. 抛物线y=2x2一条弦的垂直平分线l的斜率为2,则l在y轴上截距的取值范围为() A. (■,+∞)B.(■,+∞) C. (■,+∞)D.(■,+∞) 12. 若函数f(x)=(cosx-sinx)(cosx+sinx)+3a(sinx-cosx)+(2a+1)x在(-■,0)上单调递增,则a的取值范围为() A. [-1,■]B. [-1,■]C. [-1,■]D. [-■,1] 二、填空题:本大题共4小题,每小题5分. 13.(1+x)3(1+■)3的展开式中,含■的项的系数是_______. 14. 设点P(x, y)满足:x+y-3≤0,x-y+1≥0,x≥1,y≥1,则■的取值范围是_______. 15. 已知A、B、C、D四点在半径为■的球面上,且AC=BD=5,AD=BC=■,AB=CD,则三棱锥D-ABC的体积是_______. 16. 点P(2,2),圆C ∶ x2+y2-8y=0,过点P的动直线l与圆C交于A, B两点,线段AB的中点为M,O为坐标原点. 若OP=OM,则△POM的面积为_______. 三、解答题:共70分. 解答应写出文字说明、证明过程或演算步骤. 第17-21题为必考题,每个试题考生都必须作答. 第22、23题为选考题,考生根据要求作答. (一)必考题:共60分. 17.(本小题满分12分)已知公比不为1的等比数列{an}的前 n项和为Sn,满足S6=■且a2, a4, a3成等差数列. (1)求等比数列 {an} 的通项公式. (2)设数列{bn}满足bn=nan,求数列{bn}的前n项和为Tn . 18.(本小题满分12分)在三棱锥A-BCD中,AB=AD=BD=2,BC=DC=■,AC=2. (1)求证:面ABD⊥面BCD; (2)点P 在AC上,若二面角P-BD-A为60°,求■的值. 19.(本小题满分12分)张先生家住H小区,他工作在C科技园区,从家开车到公司上班路上有L1, L2两条路线(如图),L1 路线上有A1, A2, A3三个路口,各路口遇到红灯的概率均为■;L2路线上有B1, B2两个路口,各路口遇到红灯的概率依次为■,■.
(1)若走L1 路线,求最多遇到1次红灯的概率;
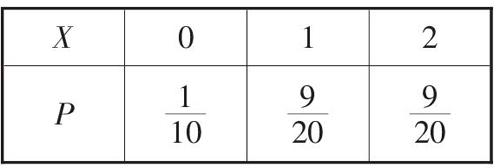
(2)若走L2 路线,求遇到红灯次数X的数学期望;
(3)按照“平均遇到红灯次数最少”的要求,请你帮助张先生从上述两条路线中选择一条最好的上班路线,并说明理由.
20.(本小题满分12分)已知■+■=1(a>b>0)的左、右焦点分别为F1,F2,F1F2=2■,点P在椭圆上,tan∠PF2F1 =2且△PF1F2的面积为4.
(1)求椭圆的方程.
(2)点B(1,■)是椭圆上的一定点,B1, B2是椭圆上的两动点,且直线BB1与BB2关于直线x=1对称,试证:直线B1B2的斜率为定值.
21.(本小题满分12分)函数f(x)=a·ex,g(x)=lnx-lna,其中a为常数,且函数y=f(x)和y=g(x)的图像在其与坐标轴的交点处的切线互相平行.
(1)求此平行线的距离;
(2)若存在x使不等式■>■成立,求实数m的取值范围;
(3)对于函数y=f(x)和y=g(x)公共定义域中的任意实数x0,我们把f(x0)-g(x0)的值称为两函数在x0处的偏差. 求证:函数y=f(x)和y=g(x)在其公共定义域内的所有偏差都大于2.
(二)选考题:共10分. 请考生在第22、23题中任选一题作答. 如果多做,则按所做的第一题计分.
22.(本题满分10分)选修4-4:坐标系与参数方程
已知曲线C1:x=cos?兹,y=sin?兹(?兹为参数),曲线C2:
x=■t-■,y=■(t為参数).
(Ⅰ)指出C1,C2各是什么曲线,并说明C1与C2公共点的个数;
(Ⅱ)若把C1,C2上各点的纵坐标都压缩为原来的一半,分别得到曲线C1′, C2′. 写出C1′, C2′的参数方程. C1′与C2′公共点的个数和C1与C2公共点的个数是否相同?说明你的理由.
23. 选修4-5:不等式选讲
对于函数f(x)= ax2+bx+c
(1)若f(x)>0的解集为{x│1
(2)若在x=-1, 0, 1三点处的函数值的绝对值均不大于1,则x∈[-1, 1]时,求证:ax+b≤2.
2020年全国高考理科数学模拟试题参考答案
一、选择题
1. D. A={x│-2 2. A. 由z1=2+i,z1·z2=2-i?圯z2=■=■-■i 所以,复数z2的共轭复数为■+■i . 3. D. 由f(x)为定义在R上的奇函数,可知f(0)=1+a = 0,∴ a=-1. 于是f(-1)=■+1-1=■,∴ f(1)=-■. 4. C. 年龄在[30,40)的委员人数为30人,所占频率为■=10b,所以b=0.02,根据频率分布直方图知(0.005+2a+0.015+0.02+0.04)×10=1,解得a=0.01,所以年龄在[60,80]之间的频率为(0.01+0.005)×10=0.15,估计年龄在[60,80]之间的委员人数为1500×0.15=225. 5. B. 不妨设右焦点F2(c,0),渐进线方程为l ∶ bx-ay=0,则点F2(c, 0)到l ∶ bx-ay=0的距离为■=b,则b=■?圯9b2=8c2?圯e=3. 6. A. 由cos(+■)=■?sin(+■)=■. 于是sin(+■)=2sin(+■)cos(+■)=2×■×■=■. cos(+■)= cos2(+■)-sin2(+■)=■, sin(+■)=sin[(+■)-■]=sin(+■)cos■-cos(+■)sin■=■. 7. C. 在A中,△A1BD为等边三角形,所以三心合一.∵AB=AA1=AD,∴ H到△A1BD各顶点的距离相等,即H为外心垂心,∴ A正确;∵CD1∥BA1 ,CB1∥DA1,CD1∩CB1=C,∴平面CD1B1∥平面A1BD. ∴ AH⊥平面CB1D1,∴ B正确;连AC1,则AC1⊥B1D1,∵B1D1∥BD,∴ AC1⊥BD同理AC1⊥BA1. ∴ AC1⊥平面A1BD. ∴ A、H、C1三点共线,∴ C正确. 8. B. 由a2=abcos C+bccosA?圯a2=ab·■+bc·■, 得a=b?圯sinA=sinB. 由a=4sinB 2RsinA=4sinB 2RsinA=4sinA R=2. sin2AsinC=■ sinAsinBsinC=■. 那么△ABC的面积S=■absinC=■(2RsinA)(2RsinB)sinC=2×22×■=■. 9. C. 由CD=■AB=4及面积为20可得梯形的高为4. 以AB为x轴,AB的中垂线为y建立直角坐标系,则A(-3, 0),B(3, 0),E(■, 2),G(-■, ■),F(-■, ■). 那么■=(-■,■),■=(■,■),于是■·■=-■×■+■×■=-■. 10. C. 由图像知A=2,T= 4[■-(-■)]=4 , 那么■= 4 , =■,所以f(x)=2sin(■+ ). 又由f(-■)=0,即2sin(-■+ )=0结合 <■,得 =■.
即f(x)=2sin(■+■), 而g(x)=2sin[■(x-■)+■]=2sin■.
由2k -■≤■≤2k +■ 4k - ≤x≤4k + ,结合选项可得C.
11. D. 设弦两端点分别为A(x1, y1),B(x2, y2),l在y轴上的截距为b,依题意得l的方程为y=2x+b;过点A、B的直线方程可写为y=-■x+m,所以x1, y2满足方程2x2+■x-m=0,得x1+x2=-■,A、 B为抛物线上不同的两点等价于上述方程的判别式△=■+8m>0,即m>-■;设AB的中点N的坐标为(x0,y0),则x0 =-■,y0 =-■x0+m=■+m.
由于N∈l,得■+m=-■+b,于是b=■+m>■-■=■.
12. D. 由于f ′(x)=-2sin2x+3a(cosx+sinx)+2a+1
=-2(cosx+sinx)2+3a(cosx+sinx)+2a+3≥0恒成立.
由于cosx+sinx=■sin(x+■),因為x∈(-■,0),得-1≤cosx+sinx≤1.
令g(t)=-2t2+3at+2a+3(-1≤t≤1),欲使g(t)≥0恒成立,只需 g(-1)≥0,g(1)≥0,即-2(-1)2+3a×(-1)+2a+3≥0,-2+3a+2a+3≥0 -■≤a≤1
二、填空题
13. 15. (1+x)3(1+■)3=(1+3x+3x2+x3)(1+■+■+■),其中含■项是1×■+3x×■+3x2×■=■. 故(1+x)3(1+■)3的展开式中含■的项的系数是15.
14.[-■,■]. 不等式组x+y-3≤0,x-y+1≥0,x≥1,y≥1所以表示平面区域,如图,根据t的几何意义,t 值即为区域内的点与坐标原点连线的斜率,显然OA的斜率■最小,OB的斜率2最大,即■≤t≤2. 由于函数 f(t)=■-t在[■,2]上单调递减,故-■≤ f(t)≤■.
15. 20. 因为AC=BD=5,AD=BC=■,AB=CD,可以构造长方体,如图设该长方体的长、宽、高分别为x,y, z由已知可得:
x2+y2+z2=(5■)2,x2+y2=25,y2+z2=41
x2=9,y2=16 =xyzz2=25=3×4×5=60.
那么,三棱锥D-ABC的体积为VABCD =V-4×■xyz=60-40=20.
16. ■. 设M(x, y),则■⊥■,
于是(x, y-4)·(x-2, y-2)=0,即N ∶ (x-1)2+(y-3)2=2此为点M的轨迹方程 .
由于OP=OM,故O在线段PM的垂直平分线上. 又P在圆N上,从而ON⊥PM. 因为ON的斜率为3,所以l的斜率为■,故l的方程为y=-■x+■.
又OP=OM=2■,O到l的距离为■,PM=■,所以△POM的面积为■.
三、解答题
(一)必考题
17.(1)设数列{an}的首项为a1,公比为q,
由题意得S6 =■,a2+a3=2a4 ■ =■,a1q+a1q2=2a1q3 a1=3,q=-■.
从而an=a1qn-1 =3(-■)n-1.
(2)由(1)得bn= 3n(-■)n-1,
由Tn=3×(-■)0+3×2(-■)+3×3(-■)2+…+3n×(-■)n-1……(1)-■Tn=3×(-■)+3×2(-■)2+3×3(-■)3+…+3n×(-■)n……(2)
(1)-(2)得■Tn =3×(-■)0+3(-■)+3(-■)2+…+3(-■)n-1-3n×(-■)n.
整理得:Tn =■-(2n+■)(-■)n.
18.(1)取BD中点E,连接AE,CE,∵AB=AD=BD=2,又E为BD中点,∴ AE⊥BD,AE=■,
同理可得:CE⊥BD,CE=1.
于是角∠AEC为二面角A-BD-C的平面角,由于AC=2得AE2 +CE2 = AC2,
即∠AEC=90°,故面ABD⊥面BCD.
(2)∵ AB=AD=BD=2,BC=DC=■,
∴ △BCD为直角三角形,且AE=■,CE=1,
∴ AE2 +EC2 = AC2,∠AEC=■,即AE⊥EC.
又AE⊥BD,所以AE⊥平面BCD,∴以E为坐标原点,EC为x轴,ED为y轴,EA为z轴建立如图直角坐标系. ∴ B(0,-1,0),D(0,1,0),C(1,0,0),A(0,0,■).
设P(x0, y0, z0),■ = ■(0≤≤1),■(1,0,-■),■=(x0, y0, z0-■),∴(x0, y0, z0-■)= (1,0,-■)=( ,0,-■ ),
∴x0 = ,y0 =0,z0 -■=-■ ,即x0= ,y0=0,z0=■-■ ,∴ P(?姿, 0, ■-■ ),
■ =( ,1,■-■ ),■ =(0,2,0).
设 ■=(x1, y1, z1)是平面BPD的法向量,
∴ ■·■ =0, ■·■ =0 x1+y1+(■-■ )z1=0,2y1=0,令z1=■,得y1=0,x1=3-■,
∴ ■=(3-■, 0, ■).
由于面PBD的法向量为 ■=(1, 0, 0),
∴cos?兹=cos< ■, ■>= ■=■ =■即■=■.
19. (1)设走L■路线最多遇到1次红灯为A事件,则:
P(A)=C 03×(■)3+C 13×■×(■)2=■.
所以走L■路线,最多遇到1次红灯的概率为■.
(2)依题意,知X的可能取值为0,1,2.
P(X=0)=(1-■)×(1-■)=■,
P(X=1)=■×(1-■)+(1-■)×■=■,
P(X=2)=■×■=■.
随机变量X的分布列:
∴ E(X)=■×0+■×1+■×2=■.
(3)设选择L■路线遇到红灯次数为Y,随机变量Y服从二项分布Y B(3,■),所以E(Y)=3×■=■.
因為E(X) 20.(1)由tan∠PF2F1=2?圯sin∠PF2F1=■,cos∠PF2F1=■. 由题意得: ■×2■·PF2×■= 4,PF12=PF22+(2■)2-2·PF2×(2■)×■?圯 PF1= 4,PF2= 2. 从而2a=PF1+PF2=4+2=6?圯a=3,结合2c=2■,得b2=4. 故椭圆的方程为■+■=1. (2)设直线BB1的斜率为k,因为BB1与BB2关于直线x=1对称,所以BB2的斜率为-k,于是BB1的方程为y-■=k(x-1),再设B1(x1,y1),B2(x2,y2). 由y-■= k(x-1),■+■=1?圯(4+9k2)x2+6k(4■-3k)x+9k2-24■k- 4=0,因为该方程有一根为x=1,于是x1=■. 同理可得x2=■. 而■=■=■=■=■=■为定值. 21.(1)由于 f ′(x)=aex,g ′(x)=■,y= f(x)的图像与坐标轴的交点为(0,a),y=g(x)的图像与坐标轴的交点为(a,0),由题意得 f ′(0)=g′(a),即a=■. 又∵a>0,∴a=1. ∴ f(x)=ex,g(x)=lnx,∴函数y=f(x)和y=g(x)的图像在其坐标轴的交点处的切线方程分别为:x-y+1=0,x-y-1=0 ∴两平行切线间的距离为■. (4分) (2)由■>■得■>■,故m 令h(x)=x-■ex,则m 当x=0时,m<0; 当x>0时, ∵h′(x)=1-(■ex+■ex)=1-(■+■)ex, ∵x>0, ∴■+■≥2■=■,ex>1,∴(■+■)ex>■. 故h′(x)=1-(■+■)ex<0. 即h(x)= x-■ex在区间[0,+∞)上单调递减,故h(x)max=h(0)=0,∴ m<0. 故实数m的取值范围为 (-∞, 0). (3)∵函数y= f(x)和y= g(x)的偏差为:F(x)= ex-lnx,x∈(0, +∞), ∴ F′(x)= ex-■,设x=x0为F′(x)= ex-■=0的解, 则当x∈(0, x0),F ′(x) < 0;当x∈(x0, +∞),F ′(x)> 0,∴ F(x)在(0, x0)单调递减,在(x0, +∞)单调递增. 故F′(1)= e-1>0,F′(0.5)=■-2<0 ∴■ 又■-■=0,故∴ Fmin(x)=■-lnx0=■+x0>2■, 即函数y= f(x)和y= g(x)在其公共定义域内的所有偏差都大于2. (二)选考题 22.(Ⅰ)C1是圆,C2是直线. C1的普通方程为x2+y2=1,圆心C1(0,0),半径r=1. C2的普通方程为x-y+■=0. 因为圆心C1到直线x-y+■=0的距离为1,所以C2与C1只有一个公共点. (Ⅱ)压缩后的参数方程分别为: C1′: x=cos ,y=■sin (?兹为参数);C2′: x=■t-■,y=■t(t为参数). 化为普通方程为C1′:x2+4y2=1,C2′:y=■x+■,联立消元得2x2+2■x+1=0,其判别式△=(2■)2-4×2×1=0, 所以压缩后的直线C2′与椭圆C1′仍然只有一个公共点,和C1与C2公共点个数相同. 23.(1)由于 f(x)>0的解集为{x│1 a<0,1+3=-■, 1×3=■■=-4,■=3,-■=2. 于是,不等式x-■+x+■>■即为x-3+x-4>2. 由x-3+x-4>2?圯x<■或x>■. 故不等式x-■+x+■+■>0的解集 {x│x<■或x>■}. (2)由 f(1)=a+b+c, f(-1)=a-b+c, f(0)=c?圯 a=■[ f(1)+f(-1)]-f(0), b=■[ f(1)-f(-1)], c= f(0). 则ax+b≤max{a+b,a-b} . 由a+b=■[ f(1)+f(-1)]- f(0)+■[ f(1)-f(-1)]≤f(1)- f(0)≤2. 同理a-b≤2. 故ax+b≤2. 责任编辑 徐国坚
