2019新型冠状病毒SEIR模型求解及MATLAB软件实现

王众 汪和松

摘要：众所周知，病毒会给社会造成巨大危害。根据这次病毒潜伏期都有传染性特点，在经典的SEIR模型上定义了潜伏者传染概率b2，并用MATLAB软件实现了数值解。

关键词：新型冠状病毒;SEIR模型;MATLAB软件

中图分类号：TP393.092 文献标识码：A 文章编号：1007-9416（2020）02-0226-01

2019年底，一种新型冠状病毒袭击了中国武汉，随之蔓延到全国。随着卫生设施的改善、医疗水平的提高以及人类文明的不断发展，诸如霍乱、天花等曾经肆虐全球的传染性疾病已经得到有效的控制，但是一些新的、不断变异着的传染病毒却悄悄向人类袭来。长期以来，建立数学模型以描述疾病的传播过程从而寻找抑制传播的方法一直是科学家们探索的方向。但是由于疾病传播的复杂性，仅能从一般的传播机理角度建立大致的传播模型，现介绍一种与这次实际情况较为接近的传染病传播模型——SEIR模型。

1 模型假设及符号说明

（1）总人数N不变。人群分为健康者、潜伏者、传染者和康复者四类。t时刻四类人数量分别记为S（t），E（t），I（t）和R（t）。（2）传染者的接触人数r;传染者传染概率b;潜伏者患病概率a;潜伏者接触人数r2;潜伏者传染概率b2;康复概率c。（3）潜伏者有传染性概率。

2 SEIR模型建立及MATLAB软件实现

2.1 SEIR模型建立

由假设1显然有：

建立关于S（t），E（t），I（t）和R（t）的四个方程：

记初始时刻的健康者、潜伏者、传染者和康复者的比例分别是，，和，则SEIR模型的方程可以写作：

2.2 模型的MATLAB软件实现

使用MATLAB软件对以上微分方程组进行求解代码如下：

seir.m脚本，

function y=seir（t，x）;

r=10;b=0.03;a=0.1;r_2=20;b_2=0.03;c=0.1;

y=[r*b*x（1）*x（3）-r_2*b_2*x（1）*x（2），r*b*x（1）*x（3）-a*x（2）+r_2*b_2*x（1）*x（2），a*x（2）-c*x（3），c*x（3）]';

End;

seirun.m脚本，

[t，x]=ode45（'seir2'，[0，160]，[0.95 0.01 0.03 0.01]）;

%ode45是用來求解常微分方程的方法。

figure（1）;

plot（t，x（：，1），'-.r'，t，x（：，2），'-.b'，t，x（：，3），'-.k'，t，x（：，4），'-.g'）

title（'SEIR模型'）;

xlabel（'时间'）;

ylabel（'人数*100000'）;

legend（'易感者'，'潜伏者'，'病人'，'康复者'，'4'）;

figure（2）;

plot（x（：，1），x（：，2））;

title（'i-s图形（相轨线） '）;

xlabel（'s'）;

ylabel（'i'）;

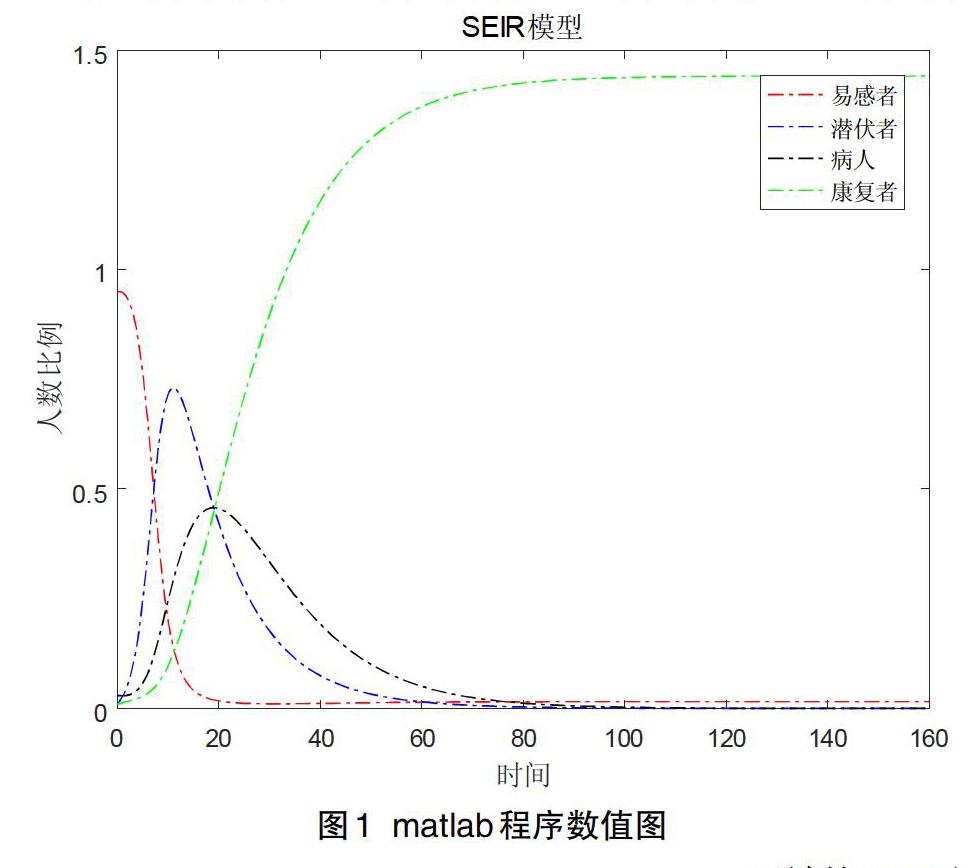
可以得到数值解及图像，如图1所示。

3 结语

本论文的模型因查到的统计数据不完善、对2019新型肺炎的传播规律了解不够，预测结果有较大偏差。相信随着人们对2019新型肺炎的进一步认识，随着社会各界的深入研究，从数学角度看，模型将更加完善，预测结果将更准确，从医学角度看，2019新型冠状肺炎将有更好的治疗方案和防控措施，疫期将进一步缩短。

参考文献

[1] 姜启源，谢金星，叶俊.数学模型（第四版）[M].北京：高等教育出版社，2011.

Solving the SEIR Model of  2019-nCov and its Matlab Implementation

WANG Zhong1，WANG He-song2

（1.Hunan Vocational College of  Electronic and Technology， Changsha  Hunan  410217;

2.Changsha University of  Science and Technology， Changsha  Hunan  410076）

Abstract：As we all know， viruses can do great harm to society.According to this incubation period， the virus is infectious，the probability of latent infection is defined on the classic SEIR model.The numerical solution is realized by MATLAB.

Key words：2019-nCov; SEIR model; MATLAB