基于局部期望最大化注意力的图像降噪

李泽田，雷志春

(天津大学 微电子学院，天津 300072)

1 引 言

图像降噪是计算机视觉中的基本问题，也是许多其他图像恢复任务的重要预处理步骤[1-6]。通常，图像降噪的目的是从其退化图像恢复出无噪声图像[7]。

图像降噪具有非适定性(Ill-posed)[8]。传统图像降噪方法[9-12]应用各种约束来模拟噪声特征(例如，均匀、非均匀、深度感知)，并利用不同的图像先验来规范解空间。然而，在大多数方法中使用的图像先验都是手工制作的,并且消耗大量的计算资源。

最近几年，随着深度卷积神经网络(Deep Convolutional Neural Network，DCNN)的发展，图像去噪性能得到了显著提升。文献[13]通过将批量归一化集成到残差网络中，提出了一种称为DnCNN(Denoising Convolutional Neural Networks)的有效图像降噪网络，该网络优于传统的降噪算法。文献[14]基于小波分解，提出了一种基于多级小波的降噪算法，称为MWCNN(Multi-level Wavelet-CNN)。文献[15]提出了一种快速灵活的网络称为FFDNet，可以处理具有不均匀噪声的图像。为了利用DCNN中图像特征的非局部性，文献[16]在去噪网络中采用k-最近邻匹配，提出N3Net算法。

由于DCNN强大的拟合能力，上述基于DCNN的降噪算法较传统算法效果提升显著。但这些算法也有其局限性。首先，采用“编码器-解码器”级联的方式构建模型，在计算每一个解码器的状态时需要关注所有的编码器输入，计算量比较大，灵活性差，网络的泛化能力较低。其次，平等地处理不同通道、不同区域的特征，效率较低，浪费有限的计算资源。最后，在DCNN中，随着图像在网络中的传播，特征域的噪声会不断累加[17]。

为克服以上基于DCNN的降噪算法的缺点，本文设计了一个基于局部期望最大化注意力的图像降噪算法。近年来，注意力机制在自然语言处理领域取得卓越成果[18]。Nonlocal[19]第一次将注意力机制应用到计算机视觉领域。RCAN[20]提出后，注意力在低层视觉领域也受到了广泛的关注。注意力机制关注图像中突出的特征(纹理细节等)，并使每个像素充分利用不同通道的语义信息，有利于提升网络效率。然而，这些注意力机制需要生成一个巨大的注意力图，其空间复杂度和时间复杂度巨大。其瓶颈在于，每一个像素的注意力图都需要对全图计算。期望最大化注意力机制(Expectation-Maximization Attention，EMA)[21]，摒弃了在全特征图上计算注意力图的流程，首先通过期望最大化(EM)算法迭代出一组紧凑的基，然后在这组基上运行注意力机制，大幅降低了计算复杂度。然而，EMA仍然是针对全图计算期望值，这对于降噪任务不是最优方案。因为噪声属于快速变化的高频信号，本文认为，应该利用特征图的局部信息提取噪声注意力图，即采用局部期望最大化(Local Expectation-Maximization Attention，LEMA)算法替代EMA算法，通过局部期望最大化(LEM)算法迭代出一组紧凑的局部基，在这组局部基上运行注意力机制，这样不仅可以有效滤除噪声，还可以进一步降低复杂度。本文把这一机制嵌入网络中，构造出轻量且易实现的 LEMA Unit，在多个数据集上取得了较好的降噪效果。本文的主要贡献如下：

(1)改进了期望最大化算法，提出了更适于降噪任务的局部期望最大化算法(LEMA)，该算法对输入的局部特征进行迭代得到一组紧凑的局部基，在这组局部基上计算注意力图可以大幅降低计算复杂度。

(2)将LEMA机制引入DCNN中，结合通道注意力与空间注意力，构造出LEMA Unit，并将LEMA Unit嵌入到自动编码器网络中，提出LEMANet模型。

本文进行了大量的图像降噪实验，以验证LEMANet的有效性。 结果表明，LEMANet在视觉质量和定量测量方面均实现了领先的降噪性能。

2 基于DCNN的图像降噪

近几年的时间里，卷积神经网络发展的一个趋势是为了获得较好的性能，不断地增加网络层数。DCNN通过堆叠多个简单的非线性单元从大量标记数据中学习高度非线性映射[22]。

自动编码器(Autoencoder)是一种无监督的学习算法，主要用于数据的降维或者特征的提取，由编码器(Encoder)和解码器(Decoder)两部分组成，每一部分均采用堆叠DCNN的方式构成。编码器将输入图像(设为x)经过加权W、映射(φ)之后提取到图像主特征y：

(1)

其中：L为编码器层数。

解码器对y反向加权WT、映射(φ)得到输出z，

(2)

其中：L为解码器层数。

反向传播过程通过反复迭代训练两组权值W、WT，使得损失函数(MSE，感知损失等)最小，尽可能保证z近似于x，即可重构输入图像x。自动编码器结构如图1所示。fθ是编码器映射，由于输入数据x中存在相关性，为了提取图像表征的关键特征，在编码过程施加“瓶颈”(Bottleneck)，即对输入数据进行压缩，提取得到关键特征y。解码器负责由特征y解码恢复出重构数据z。在文献[23-25]中，采用降噪自动编码器(Denoising Autoencoder，DAE)方法进行高斯噪声去除，并获得与BM3D[26]、K-SVD[27]等传统算法相当的结果，显示了自动编码器方法的降噪潜力。

图1 自动编码器结构图Fig.1 Structure of autoencoder

3 局部期望最大化注意力机制

3.1 局部期望最大化算法

期望最大化(Expectation-Maximization，EM)[28]算法旨在找到隐含变量模型的最大似然解。用Y表示观测变量的数据，Z表示隐含变量的数据，Y和Z一起构成完全数据。假设观测数据Y概率分布为P(Y|θ)，其中θ是模型待估计的参数，Y和Z的联合概率分布为P(Y,Z|θ)。一般情况下，Z的分布未知，在θ给定的情况下，通过后验概率P(Z|Y,θ)迭代得到。完全数据的似然函数为lnP(Y,Z|θ)，EM算法通过迭代的方法求lnP(Y,Z|θ)的极大似然估计，每次迭代分两步：E步和M步，不断重复E步和M步，直到收敛。

在E步，根据给定的θ通过后验概率P(Z|Y,θ)求得Z的分布，然后求完全数据的似然函数的数学期望EZ|Y,θ：

(3)

式中：θi为第i次迭代的模型参数，θi+1为第i+1次迭代的模型参数。

在M步，求使式(3)极大化的θi，确定第i+1迭代的参数估计值θi+1，

θi+1=argmaxθEZ|Y,θi，

(4)

式中argmax为极大值函数。

考虑到图像不同区域的噪声分布并不一定是均匀的，所以本文提出在图像局部应用期望最大化机制，其结构如图2所示。首先采用边缘检测，区分不同的噪声区域[29]。然后在每一区域内部应用期望最大化机制，迭代出一组紧凑的局部基，为后续计算注意力特征图做准备。最后，在局部基上计算注意力特征图：

LEM(z)=φlocal([E(z),M(z)])，

(5)

其中：LEM(z)为局部基，φlocal为局部噪声检测算子，[E(z),M(z)]为期望最大化算子。

图2 局部期望最大化注意力模块Fig.2 Local expectation-maximization attention module

3.2 通道注意力

网络的浅层特征包含丰富的高频信息，这对降噪后图像细节的恢复非常重要，但这些高频信息在特征通道间被平等对待，这阻碍了网络的表达能力。为克服这一缺点，本文将通道注意力机制引入到图像降噪中。

通道注意力主要关注输入的抽象信息[30]。输入图像各特征通道间的信息有高度相关性，利用这一相关性，滤除通道冗余信息，使网络专注于关键信息。生成通道注意力，不仅可以提高网络性能，还可以降低网络复杂度。为了有效计算通道注意力，需要对输入特征图进行降维，即减少冗余信息，主要是低频信息。常用的降维方法是利用均值池化[31-32]，但是均值池化在滤除低频的同时，会损失一些高频信息。为此，本文同时使用了均值池化与最大池化，实验证明效果比单独使用均值池化性能优异。通道注意力满足方程：

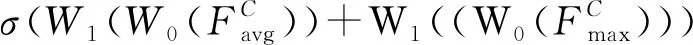
(6)

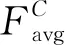
图3 视觉质量对比。图像噪声水平为25的降噪结果。Fig.3 Visual quality comparison. Denoising results of one image from BSD68 with noise level 25.

图4 视觉质量对比。图像噪声水平为50的降噪结果。Fig.4 Visual quality comparison. Denoising results of one image from BSD68 with noise level 50.

图5 通道注意力模块结构Fig.5 Structure of channel attention moduel

3.3 空间注意力

MS(F)=σ(f7×7
([AvgPool(F);MaxPool(F)]))，

(7)

式中：σ为Sigmoid函数；f7×7() 为7×7的卷积操作；AvgPool()为均值池化函数；MaxPool()为最大池化函数；[;]表示通道维度上特征的连接操作。

空间注意力模块的结构如图6所示。

图6 空间注意力模块结构Fig.6 Structure of spatial attention moduel

3.4 全局注意力网络

在卷积神经网络中，设卷积核为n×n，则该层卷积只关注邻域为n的区域，即使通过增加层数、采用扩张卷积使感受野越来越大，也难以学习全局语义信息[19]。全局注意力网络就是提取全局特征，也就是图像中任何像素在当前像素的映射的叠加。

全局注意力满足方程：

(8)

全局注意力网络如图7所示，其结构由3部分组成：(1)注意力生成，采用1×1卷积和softmax函数来获取注意力权重，然后与输入特征图相乘得到全局注意力特征；(2)特征传递，此部分采用1×1卷积、实例归一化和非线性激活层(ReLU)级联的方式；(3)全局注意力聚合，得到全局注意力。该模块中的1×1卷积可以实现特征数的压缩，从而降低计算复杂度。

图7 全局注意力模块结构Fig.7 Structure of global attention network

4 局部期望最大化注意力网络

局部期望最大化注意力网络，利用局部期望最大化机制迭代出一组紧凑的局部基，然后在这组局部基上利用通道注意力模块提取图像的抽象信息，即图像中的内容；利用空间注意力模块提取图像中的位置信息，即图像中各要素间的相对位置。全局注意力模块负责计算图像中所有像素点对于某一特定像素的映射，其中全局池化操作可以提高网络的拟合能力，减少网络层数，加速训练。

局部期望最大化注意力网络由5部分组成：(1)浅层特征提取模块，由一个3×3的卷积层构成，用于提取浅层特征，这些特征包含大量的高频信息；(2)深层特征提取模块，用于提取深层特征，这些特征包含抽象信息，由一个自动编码器Autoencoder构成，Autoencoder采用的是Encoder-Decoder结构；(3)局部期望最大化模块，用于迭代出一组紧凑的局部基；(4)注意力模块，由通道注意力、空间注意力网络及全局注意力网络构成；(5)图像重建模块，由一层卷积核大小为1×1的卷积层构成，因为生成的是彩色图像，所以输出通道为3。整个网络结构如图7所示。

图8 全局双注意力网络结构Fig.8 Structure of global dual attention network

通道注意力模块与空间注意力模块中采用最大池化与均值池化操作,突出主要特征，抑制次要特征，生成通道注意力与空间注意力。全局注意力模块采用全局池化提取图像全局特征，生成全局注意力。由于抑制了对降噪任务贡献较小的次要特征，因而使用注意力机制降低了特征图计算复杂度。

5 测量实验与结果

为了验证本文推出的局部期望最大化注意力网络的降噪性能，进行了多次实验，并与其他现有的降噪模型进行了全面对比，包括深度学习和非深度学习的方法：BM3D[26]、WNNM[12]、DnCNN[13]、FFDNet[15]、N3Net[16]。

5.1 实验参数与数据集

5.1.1 参数设置

浅层与深层特征提取模块，卷积核尺寸为3×3，歩长为1，特征通道数为64；全局特征提取模块，卷积核尺寸为1×1，歩长为1，特征通道数为128；图像重建模块，卷积核尺寸为1×1，歩长为1，特征通道数为3。

训练集原图使用DIV2K数据集[33]，该数据集来自CVPR NTIRE 2017挑战的高质量(2K分辨率)图像数据集。DIV2K数据集包含800个训练图像，100个验证图像和100个测试图像。噪声图则依据文献[14]，生成3种噪声等级的噪声图，即σ=15，25，50。测试集使用3个标准数据集：Set12[17]、BSD68[34]和Urban100[35]。实验结果测试指标在YCbCr空间的Y通道上用峰值信噪比(PSNR)和结构相似性指数(SSIM)[36]评价。

5.1.2 实验细节

对800个训练图像进行数据增强，训练图像随机旋转90°，180°，270°并进行水平翻转。在每个训练批次中，提取16对64×64的原图与噪声图作为输入。训练过程中，使用ADAM优化器[37]最小化损失函数。初始学习率设置为1E-4，并随训练过程呈指数衰减，衰减系数为0.9。

5.2 实验参数与数据集

与5个最先进算法进行了对比实验：BM3D[26]、WNNM[12]、DnCNN[13]、FFDNet[15]、N3Net[16]。测试集为Set12[13]、BSD68[34]和Urban100[35]。实验结果如表1所示。可以看出，本文提出的LEMA的PSNR值比其他最先进算法均有显著提升。σ=25时，对于测试集Set12，LEMA的PSNR值比传统方法BM3D和WNNM提升0.36～0.67 dB左右，比DnCN提升0.20 dB左右，比FFDNet提升0.21 dB，比N3Net提升0.06 dB。在数据集BSD68与Urban100上，LEMA均表现出较明显的提升。

视觉质量对比实验如图3、图4所示。可以看出，相较于其他算法，LEMA的降噪效果明显，保留更多的细节信息。

表1 与最先进算法对比实验Tab.3 Performance comparison with the state of the art

6 结 论

本文提出了一种基于局部期望最大化注意力的图像降噪网络，该网络利用期望最大化在图像局部迭代出局部基，然后在局部基上采用注意力网络，在保证精度的同时，大大降低特征图的计算复杂度。与最先进的降噪算法对比显示该算法的性能提升明显。σ=25时，对于测试集Set12，LEMA的PSNR值比传统方法BM3D和WNNM提升约0.36～0.67 dB，比DnCN提升约0.20 dB，比FFDNet提升0.21 dB，比N3Net提升0.06 dB。在数据集BSD68与Urban100上，LEMA也均表现出较明显的提升。