基于模糊综合评价的年度用水总量考核评价研究

夏丽丽 张 聃

(1.江西省水利科学研究院，江西 南昌 330029；2.江西省水土保持科学研究院，江西 南昌 330029)

为实现社会经济的可持续发展，2012年国务院发布了《关于实行最严格水资源管理制度的意见》，提出了2015年和2030年的用水总量控制、用水效率控制和水功能区限制纳污控制“三条红线”主要目标，目前“三条红线”控制指标已被分解到省、市、县三级。为推进最严格水资源管理制度的落实，2013 年国务院颁布了《实行最严格水资源管理制度考核办法》，启动对各省、自治区和直辖市落实最严格水资源管理制度情况的考核，各省对所辖市县开展考核工作。用水总量控制是“三条红线”中最核心、最重要的控制指标[1]，其实施效果会对最严格水资源管理制度的落实产生关键影响。但年度用水总量是个变量，受降水量、灌溉面积、工业增加值、万元工业增加值用水量、总人口、人均生活用水量、城镇化率等多方面因素影响[2]。如何参照目标值对用水总量进行考核，如何判定用水总量上报值的合理性，如何令考核结果体现公平合理，目前暂无定论，国内部分学者对此问题开展了探讨和研究。曾祥等[3]构建了基于水资源利用技术效率的区域用水目标水量测算模型，利用随机前沿生产函数对用水总量控制作了实证研究；吴书悦等[4]从水资源、社会、经济和环境4个方面出发，构建了包括人均水资源量、水资源开发利用率、区域缺水率等13个基础指标的区域用水总量控制评价指标体系，运用层次分析法建立了用水总量控制模糊综合评价模型；甘泓等[5]建立了以用水量特性曲线(S-P曲线)为基础的年度用水总量考核方法。

用水总量分析评价的研究方法以层次分析法和模糊综合评价法相结合居多。模糊综合评价法是一种基于模糊数学的综合评价方法，基本思想是根据多目标评价问题的性质和目标，采用层次分析法将问题本身按层次分解，根据模糊数学的隶属度理论把定性评价转化为定量评价，具有结论清晰可靠，系统性强等特点，能较好地解决模糊的、难以量化的问题，适合各种非确定性问题的解决[6-8]。用水总量的影响因素较复杂，且各因素具有一定的模糊性和不确定性，本文综合考虑评价方法的可行性与实用性，采用层次分析法将各因素逐层分解，选取易获取的典型指标定性分析农业、工业、生活和环境4类单项用水量合理性，再利用模糊综合评价法将结论量化，从而系统全面地反映用水总量的合理性。

1 研究方法

1.1 指标选取和层次分析

目前对用水总量合理性分析多采用定额分析法、对比分析法、趋势分析法等逻辑关系检验法[9]，即从单位用水量合理性、与相关指标逻辑关系的合理性和变化趋势合理性等方面进行分析，影响用水量变化的因素较多，按照数据是否方便获取、与单项用水量的相关性是否较高的原则，选取了部分影响因子，并构建了层次分析结构，见图1。顶层为目标层(A层)，即用水总量数据合理性；第2层(B层)按照用水类别分为4项；第3层(C层)为各单项用水量的细分；第4层(D层)为采用不同方法对各单项用水量进行合理性分析的结果，其中各单项用水量不同方法选取的主要影响因子详见表1。

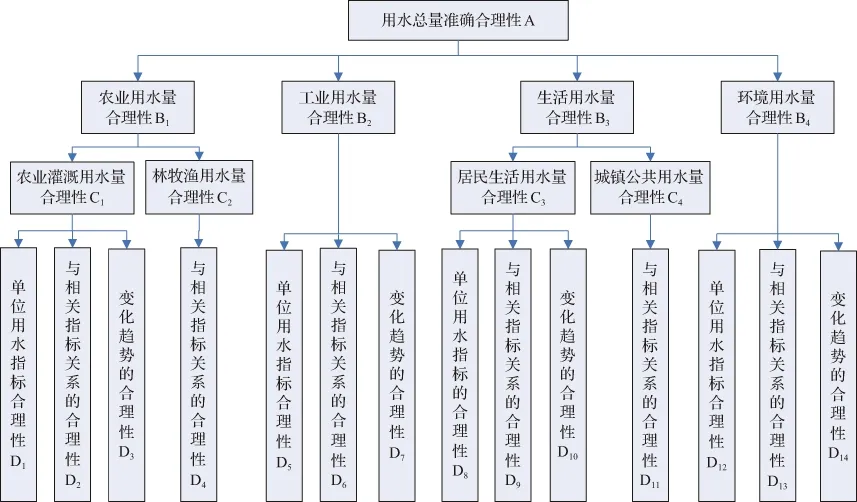
图1 层次结构

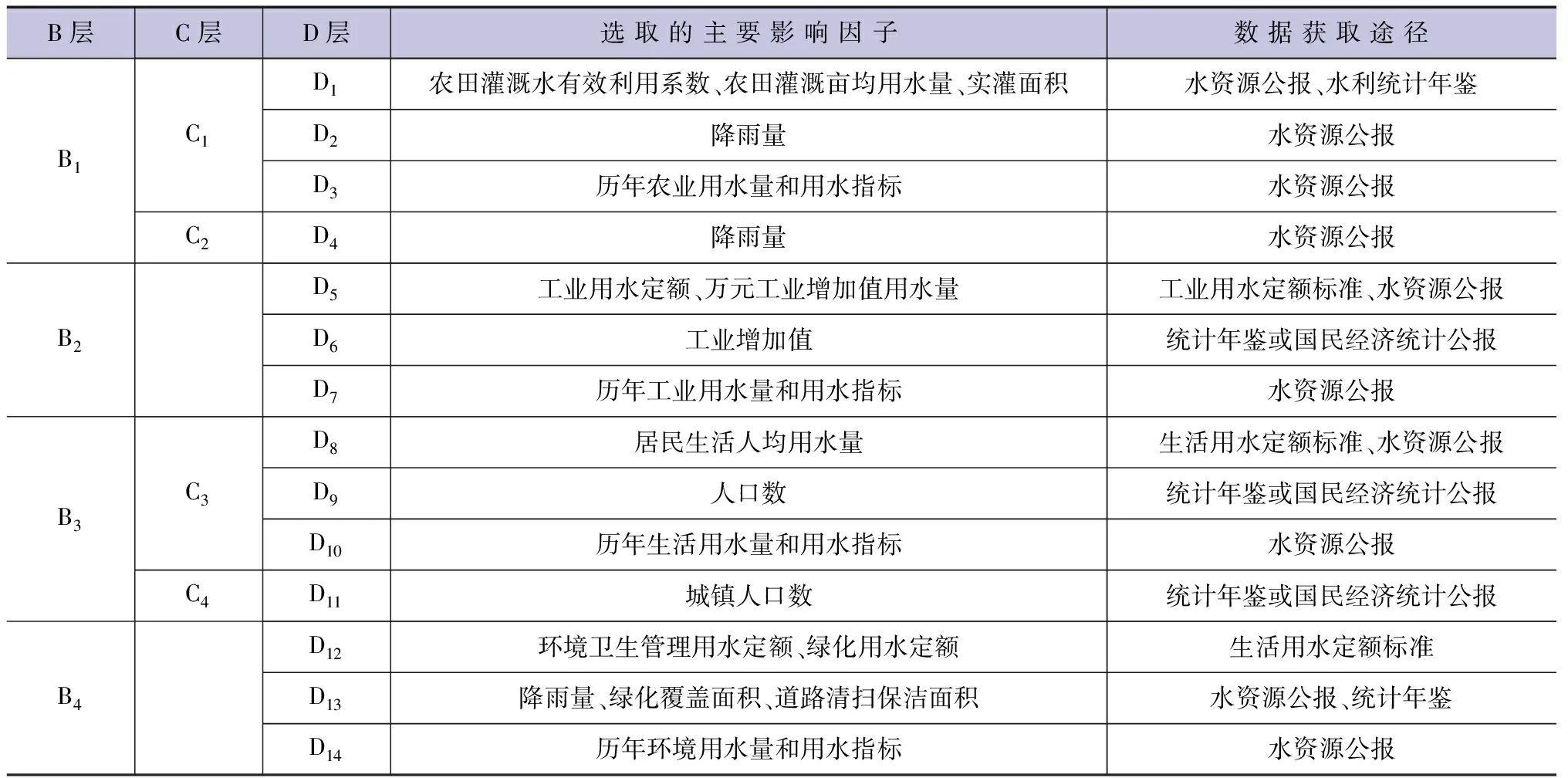
表1 单项用水量主要影响因子统计

1.2 判断矩阵和确定权重

为体现各单项用水量和各类评价内容在综合评价过程中的重要程度，通过构造判断矩阵对其赋予不同的权重系数。采用1～9标度法对D层各因素之间的重要性进行比较,见表2。

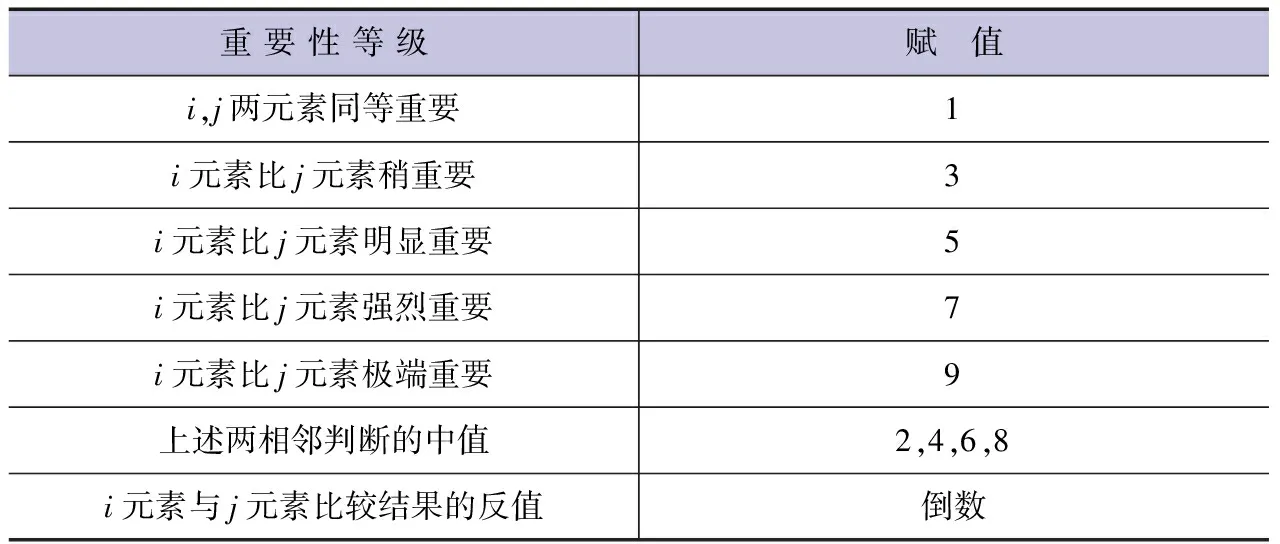
表2 1-9标度法

在构造的各层指标体系中，B层的权重分配为反映各市县用水量的差异性，采用各市县的用水构成比例作为B层的权重值，即农业、工业、生活和环境各类用水量在用水总量中的占比值。C层权重分配采用该类用水量在相应单项用水量中所占比例作为权重值。D层权重分配，除林牧渔用水量合理性和城镇公共用水量合理性的两个指标构成较为单一外，其他指标均采用判断矩阵确定权重值。按照对用水量合理性分析的贡献大小，D层核算指标的重要性顺序为：单位用水指标合理性>与相关指标关系的合理性>变化趋势的合理性，因此各指标层的判断矩阵C1-D、B2-D、C3-D、B4-D均为

根据判断矩阵计算各层次与之有联系的元素重要性次序的权值。步骤如下：

a.计算判断矩阵每一行元素的乘积Mi:

(1)

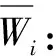
(2)

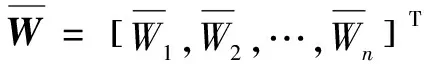
(3)

则W=[W1,W2,…,Wn]T即为所求的权系数。

然后对判断矩阵的一致性进行检验，首先计算判断矩阵A的最大特征值λmax：

(4)

(AW)i表示向量AW的第i个元素。

再计算判断矩阵的一致性指标CI:

(5)

最后计算随机一致性比率CR:

(6)

式中：RI为平均随机一致性指标。

对于1～9阶判断矩阵，RI的值见表3。

表3 RI取值

当CR<0.1时，即认为判断矩阵具有满意的一致性，否则就需要调整判断矩阵，使之具有满意的一致性。

依据上述方法，各个判断矩阵C1-D、B2-D、C3-D、B4-D计算结果均为

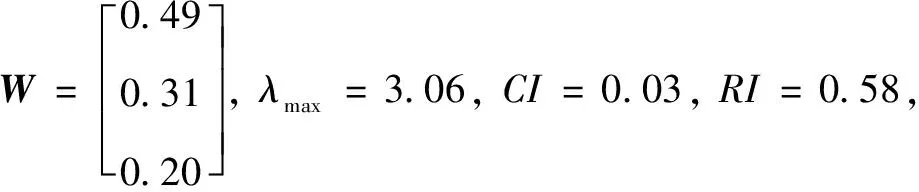
CR=0.0005

各判断矩阵的CR<0.1，可见各判断矩阵均具有满意的一致性。

依次沿递阶层次结构由上而下逐层计算，即可计算出最底层因素相对于最高层的相对重要性排序值，即权系数。层次结构中D层的权重见表4。

表4 D层权重值

通过构建模糊综合评判模型，对各因素进行量化分析，最终判定用水总量的合理性，步骤如下：

a.确定评价对象的因素论域U=(u1,u2,…,um)。本文共计14项指标。

b.确定评语等级论域V=(v1,v2,…,vn)。按照评价需求，将评语等级划分为3级：V=(非常合理，基本合理，不合理)。

对单位用水量合理性判定采用误差分析，如上报值与预估值之间误差控制在1%以内为非常准确，误差在1%～5%以内为基本准确，超出5%为不准确；趋势相符极好为非常合理，趋势基本相符则为基本合理，趋势不相符则不合理。

对与相关指标逻辑关系合理性和趋势变化合理性的判断，采用一票否决的方式，即多个相关指标中，若存在与某项相关指标逻辑关系不合理的情况，则该项指标评价结果为不合理。

c.进行单因素评价，建立模糊关系矩阵R：

(7)

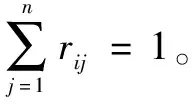
d.确定评价因素权向量F=(f1,f2,…,f12)，本次研究采用层次分析法确定权向量。

e.模糊合成估计结果分析。F中不同行反映了被评价事物从不同的单因素来看对各等级模糊子集的隶属程度。用模糊权向量F将不同的行进行综合，就可得到该被评事物从总体上来看对各等级模糊子集的隶属程度，即模糊综合评价结果向量。模糊综合评判的基本模型为B=F·R。

1.3 评判结果分析及处理

模糊综合评判计算结果以模糊向量形式体现，采用最大隶属度原则处理得到用水总量合理性的评判结果。所谓最大隶属度，即计算出的B=F·R中3个元素，即B=(b1,b2,b3)，按照评语等级论域V=(非常合理，基本合理，不合理)进行分析，最大的元素对应的评语等级即为用水总量数据合理性的评判结果。若用水总量数据合理性评判指标为“非常合理”或“基本合理”，则可采纳并用于考核；若用水总量数据合理性评判指标为“不合理”，则需要该地区进一步复核用水总量数据并重新上报，直到评判结果合理为止。

2 实例应用

以江西省萍乡市2017年用水总量上报值为例，对上述构建的用水总量合理性分析模型进行验证。

2.1 区域概况

萍乡市地处江西省西部湘赣边界，是典型的工业城市，水资源短缺情况比较严重[10]。据2013—2017年《萍乡市国民经济和社会发展统计公报》《萍乡市统计年鉴》和《江西省水资源公报》统计，萍乡市主要用水情况见表5，其中2015—2016年的数据用于评价分析，2017年数据用于模型评价结果的验证。

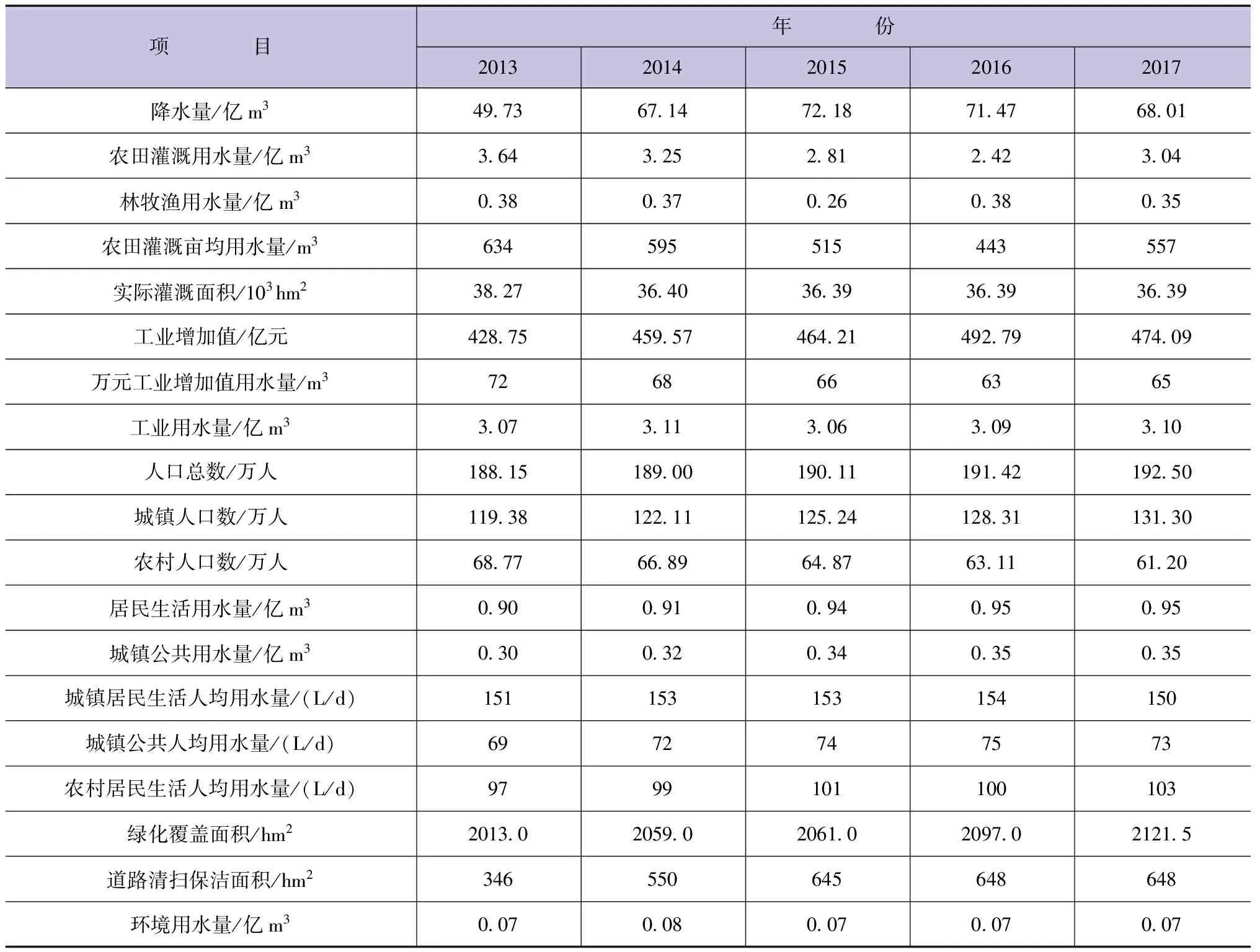
表5 萍乡市主要用水情况统计

2.2 计算分析

根据表5中的用水指标，利用定额分析法、对比分析法、趋势分析法等方法进行分析，得出各项指标分析结果，建立模糊关系矩阵R，各级指标权重见表6。

计算模糊综合评价结果向量B=F·R,其中A为用水量评价的权向量。

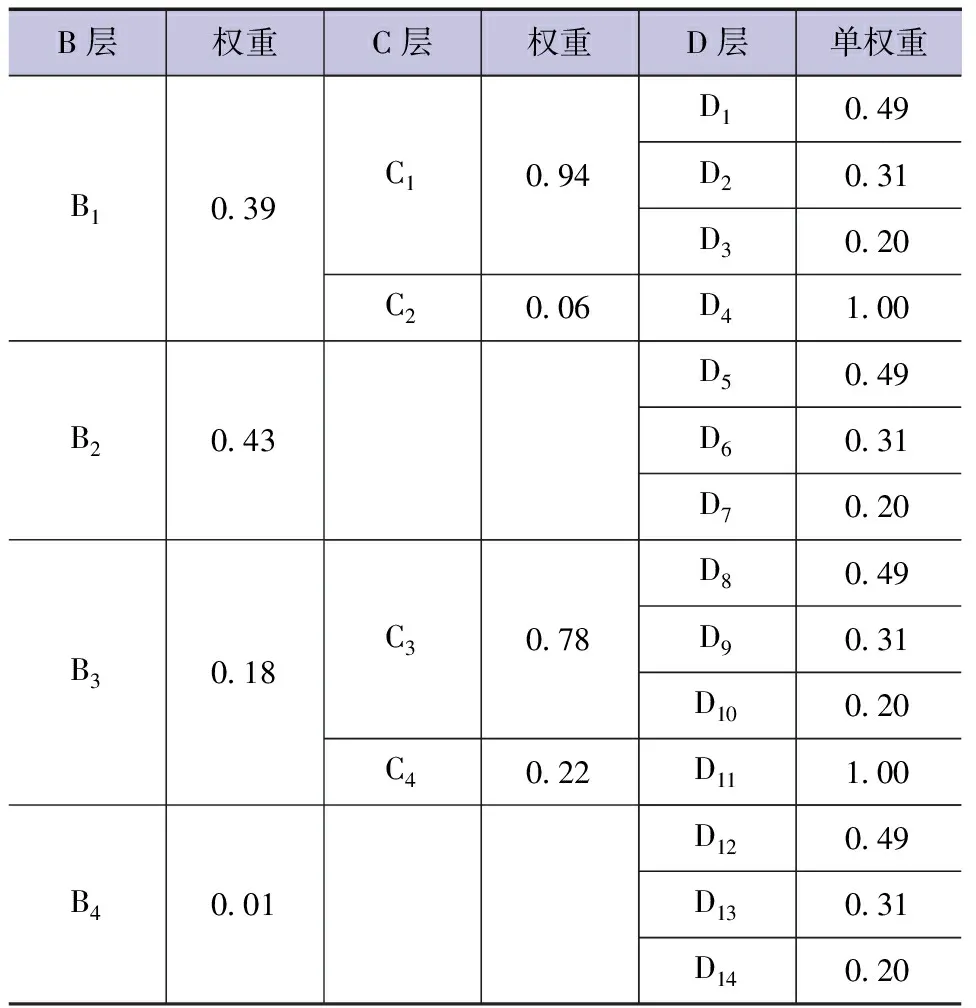
表6 萍乡市用水量合理性模糊评价指标权重

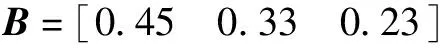
按照最大隶属度原则综合判断得出，萍乡市2017年用水总量上报值非常合理，通过与2017年《萍乡市水资源公报》相关数据对比分析，确定用水总量合理性分析模型计算得出的结果可信可用。

2.3 评价结果处理

萍乡市上报用水总量数据评价结果为非常合理，但评价结果中不合理的元素为0.23，占比较高，说明萍乡市上报的单项用水量中存在不合理因素，主要体现在3个方面：农业灌溉用水单位用水指标不合理；林牧渔用水量与降水量等相关指标关系不合理；城镇居民生活用水量变化趋势不合理。因此需萍乡市进一步复核并补充说明具体原因，若经过复核需要修正某单项用水量数据，则需要重新对该单项用水量进行合理性分析评价。鉴于萍乡市上报用水总量数据质量评价结果为非常合理，不合理之处仅为部分单项用水量评价指标，因此在萍乡市补充说明具体原因的同时，可进一步将萍乡市上报用水总量与该市用水总量控制指标目标值进行对比，分析是否符合要求：2017年萍乡市用水总量控制指标为8.82亿m3，用水总量上报值为7.61亿m3，在控制指标要求范围内，符合用水总量控制红线管理要求。

3 结 语

本文构建的年度用水总量考核评价模型，既包含了对单位用水指标的定量分析，又包含了与其他指标相关性和年际变化趋势合理性等定性分析。同时，通过对单项用水量合理性分析，可以明晰问题出处；具有采用指标数据易获取、各项指标分析易操作、基层用水总量统计人员易上手、分析结果易理解等优点，可广泛应用于水资源考核时，基层对用水总量上报数据的校核、省市级水资源考核人员对用水总量数据的考核评价等方面，对提升用水总量上报的质量和考核结果的公平合理性具有一定的实用价值。

为使用水总量考核结果更加准确合理，各级水行政主管部门仍需加强对各行业用水户的用水监管，完善用水计量设施、健全用水统计台账，从源头上提高用水数据的质量，为进一步落实最严格水资源管理和国家节水行动方案奠定基础。