基于遗传算法的火箭弹对面目标的弹着点分配方案

李彩峰，徐 锋，张玉梅，刘娟娟，范雪峰

（北方自动控制技术研究所，太原 030006）

0 引言

火箭炮射击的面目标是指正面和纵深超过一发火箭弹覆盖范围的目标。要实现对目标的全覆盖就需要多发火箭弹进行射击，此时就涉及到如何确定弹着点在目标上的相对位置。由于火箭炮的射击存在误差，对目标位置的观测也存在误差，因而在实际计算过程中需要考虑的问题是：在一定误差条件下，如何确定若干发火箭弹的预定打击位置，使得对目标造成最好的毁伤效果。

在实际应用中，一般将火箭弹的分火点均匀分配到面目标上，这种分配方式虽然考虑到了目标“面”的特性，但是却忽略了火箭弹射击误差和目标观测误差，导致在误差较大的情况下分火点的位置本来应该远离目标观测中心，但却和误差较小的情况下一致；在参考文献［4］中指出可以考虑火箭弹的射击误差，构建火箭弹对目标的有效毁伤面积模型，从而使用最优化的方法将分火点较优地分配到目标面上，但是它并没有考虑目标观测误差的影响，同时未提及使用何种最优化方法。针对以上缺陷，本文综合考虑火箭弹的射击误差和目标的观测误差，使用概率方法构建火箭弹分火点和火箭弹对目标有效毁伤面积的函数关系。由于构建出的函数较复杂，在对面目标进行微元计算时计算量巨大，无法使用传统的精确求解方法，考虑到遗传算法是一种求解近似最优解的良好算法，并且相比于传统优化算法从单个初始值迭代求最优解容易误入局部最优解的缺点，遗传算法从串集开始搜索，覆盖面大，利于全局择优，故本文采用遗传算法对该模型进行求解。下面首先提出火箭弹射击误差和目标观测误差的描述方法。

火箭弹的射击误差一般使用射弹散布概率偏差表示。射弹散布概率偏差是指在射弹散布面上，与散布轴对称，弹着点出现概率为50%的区间概率的一半，具有高低、方向和距离射弹散布概率偏差之分，使用字母E 表示，单位为m。在二维平面中，以散布中心为原点，以射弹正面为X 轴，纵深为Y轴建立直角坐标系，射弹落点相对于其散布中心的坐标是一个二维随机变量，且其密度函数如下：

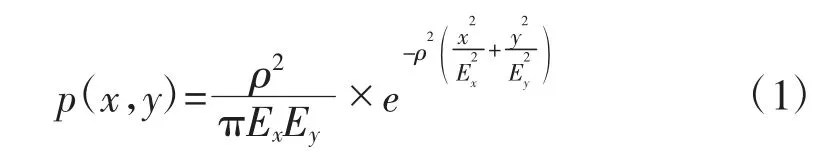
其中，ρ 是一常数，ρ=0.477，Ex表示射弹的距离概率偏差，Ey表示射弹的方向概率偏差。进行如下的随机变量替换：

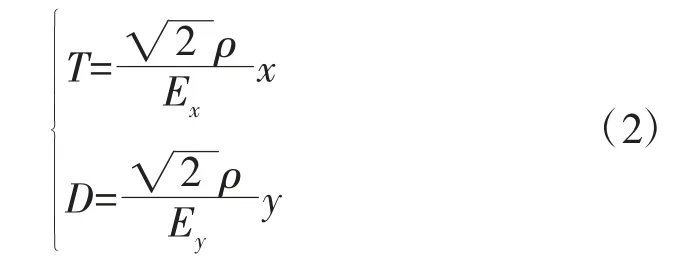
可知二维随机变量（T，D）服从如下的二维正态分布：

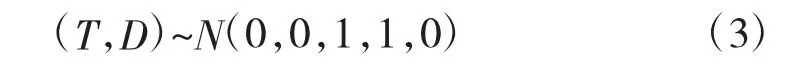
即随机变量T、D 相互独立且服从标准正态分布。

目标的观测误差也使用散布概率偏差衡量，假设目标正面、纵深与射弹的正面、纵深一致，则以目标中心、射弹正面、射弹纵深建立直角坐标系，也可以得出目标中心与其正面散布偏差和纵深散布偏差关系类似上面的结果。

1 计算目标的有效毁伤面积

在未对目标进行射击时，需要预先估计火箭弹的毁伤面积，此处提出有效毁伤面积的概念。假设火箭弹在其毁伤区域内的毁伤均匀，由于目标的观测存在误差，设平面中任意一点在目标范围内的概率为Pm（x，y），同时火箭弹存在散布误差，设该点被火箭弹覆盖的概率为P1（x，y），则可知该点同时在目标范围内和火箭弹覆盖范围内为射击有效，即有效面积为：

由此可知有效面积由上述的两个概率决定，下面对Pm（x，y）和P1（x，y）进行求解。

1.1 平面中任意一点在目标范围内的概率

假设目标为一矩形，其正面长度为D，纵深长度为F，以目标观测中心为原点，目标正面方向为X轴，纵深方向为Y 轴。由式（1）可得目标实际中心偏离观测中心的概率密度函数，在该坐标系中任取一点P（x，y），以该点为中心，两边分别平行于X 轴、Y轴，长度分别为D、F 的矩形，记该矩形区域为Ω，则当目标观测中心实际位置落到区域Ω 中时，点P 处于目标内。即点P 在目标范围内的概率为：

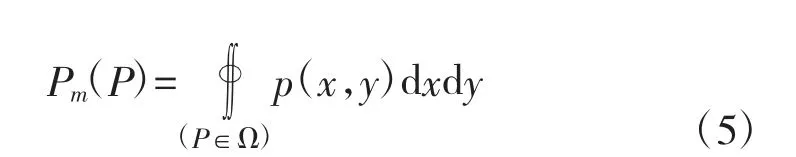
将式（2）、式（3）带入式（5）可得：

1.2 平面中任意一点被火箭弹覆盖的概率

假设火箭弹的毁伤区域为（Lx×Ly）的矩形，多发火箭弹类型一致且射击相互独立，同时目标正面、纵深和射弹正面、纵深一致，因而可以在1.1 节中构建的坐标系内进行处理。设第i 发火箭弹计划的弹着点位置，即散布中心，为Qi（xi，yi），任取点P（x，y），则该点相对于散布中心的坐标为（x-xi，y-yi），根据式（6）可得点P 被第i 发火箭弹覆盖的概率为：

从而可得点P 被火箭弹覆盖的概率为1，减去其不被任意一发弹覆盖的概率，即：

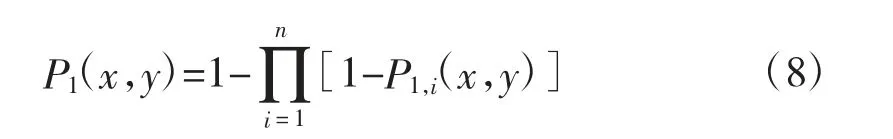
式（8）中，n 表示发射的火箭弹总数。

2 使用遗传算法计算近似最优值

根据引言中所述对火箭弹射击目标的描述，结合第1 节的描述，可以抽象出如下问题：如何确定n发火箭弹的位置（Q1，Q2，…，Qn），使得火箭弹对目标的有效毁伤面积S1最大。即：

在该最优化模型中，目标函数的自变量数目较多，目标函数复杂，很难通过解析的方法求得最优解，遗传算法可以较好地解决这类问题。同时，火箭弹的数量未确定，需要计算同一目标不同数量火箭弹的毁伤面积，以获得更优的结论。

2.1 确定变量的取值范围

2.2 对变量进行编码和解码

将0 到nx+1 范围内的整数一一映射到固定长度的二进制数中，以其中数值位数最长的二进制数值的长度作为二进制码的长度，不足位数的二进制数值前面补足0，这使得变量从取值范围的左界到有界每经过一个精度就对应一个二进制数，如此就构建了一一对应，实现了坐标点X 坐标的编码gx，Y坐标的编码gy确定原理同上。这个一一对应关系就确定了编码和解码规则。将具有固定位数的二进制数视为基因序列，二进制数的每一位值即为一个基因。

2.3 基因串的适应度评估

将二进制数值作为基因串之后，要确定种群的规模，即表征同一个变量的基因个数，该过程由随机函数生成，本文选定种群规模为50，每个基因串都具备适应度fi。适应度是一种评估基因串是否适应环境的一个表征值，在最优化问题中，适应度即将基因串解码成数值后，带入最优化函数的数值，即：

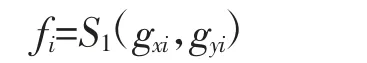
适应度越大，就表示该基因串更有可能遗传下去。

2.4 基因的突变

基因突变是克服迭代算法过早收敛的一个重要途径。遗传算法中的基因突变首先要确定基因突变的概率p，设每个基因串的长度为n，则每次要突变的基因的个数为50×n×p，将所有的基因串排成一整串，随机选取上述数目的位置，将该位置的基因的数值进行如下变换：

2.5 基因的遗传

每个基因串都具有其适应度，适应度越大的基因越容易遗传给下一代，通过归一化方法求解出每个基因遗传给下一代的概率：

当确定了基因串被遗传的概率后，通过随机方法将基因串复制到下一代，保证遗传概率高的基因串被复制的概率也高，如此进行若干代之后，适应度低的基因串就会被逐渐淘汰，适应度高的基因串就会在种群中扩散［5-7］。

在进行若干代迭代后，种群中基因串的适应度趋向于稳定，通过设定遗传的最大代数和最优值浮动的幅度大小可以控制算法的结束。

3 模型的仿真与实验结果分析

在实际情况下，弹着点的位置受目标大小和误差大小影响，而同一种火箭弹的误差一般为定值，同时在精确制导的条件下，其误差相对较小。在本文的仿真实验中，假设火箭弹的毁伤区域为（200 m×200 m），其距离概率偏差Ex和方向概率偏差Ey分别为15 m 和15 m，在此条件下，弹着点分配就随着目标观测误差的变化而变化，因而本文着重考虑以下情况下弹着点的分配问题：

1）目标1：面目标，其区域范围为（400 m×400 m），其正面散布偏差和纵深散布偏差较小，分别为10 m和10 m。

2）目标2：点目标，其区域范围为（50 m×50 m），其正面散布偏差和纵深散布偏差较大，分别为100 m和100 m。

3）目标3：线目标，其区域范围为（500 m×50 m），其正面散布偏差较小，纵深散布偏差较大，分别为10 m 和100 m。

上述3 种目标的选取基于如下依据：观测误差相对于目标而言较大时，目标中心散布区域较大，使得目标有概率出现在远大于目标观测区域的位置。而对点目标而言，如果观测误差较小，仅需要考虑弹着点位置在目标中心即可；对线目标而言，如果其观测误差较小，则弹着点位置在目标中轴线上呈均匀分布。而当这两种目标的观测误差较大时，它们就具备了面目标的特性，可以使用本文构建的模型求解弹着点位置。

考虑散布误差的情况下，一发火箭弹在平面上的毁伤概率图如下页图1 所示，该图使用等高线的形式表示毁伤概率图，其中每条等高线上的数值表示该线上的点被该发火箭弹覆盖的概率。可以看出，点被火箭弹覆盖的概率随着其距离散布中心的距离增大而逐渐降低，且在正面或纵深方向超出散布中心130 m之后的区域上的点被火箭弹覆盖的概率不足0.1。

图1 一发火箭弹的毁伤概率图

下面的几个表格列出了本文仿真结果，给出了若干发火箭弹在目标上的弹着点分配坐标，坐标原点为目标观测中心，X 轴方向与目标正面平行，Y 轴方向与目标纵深方向平行，同时给出了有效毁伤面积以及有效毁伤面积占目标总面积的比值，本文将该比值称为有效毁伤效率。

除了上述3 个目标的仿真结果，本文还对观测误差较小的点目标和线目标进行了仿真，均能计算出弹着点位置，并且对点目标而言，弹着点位置总是位于目标观测中心；对线目标而言，弹着点总是在目标中轴线上均匀分布，这种分法与实际情况相符，故而本文不将其列出。

由对目标1 的仿真结果可知，在弹数为1、2、4发时，本文所用模型计算出的弹着点位置符合均匀分布的特点，当弹数为3 发时，均匀分布和仿真结果所生成的弹着点位置如图2 所示。

图2 均匀分布（左）和仿真结果（右）的弹着点位置图示

表1 目标1 的仿真结果

表2 目标2 的部分仿真结果

表3 目标3 的部分仿真结果

同时，比较两者的有效毁伤面积可知仿真结果所得的弹着点造成的有效毁伤面积更大。

分析目标2 和目标3 的仿真结果可以看出，当目标观测误差较大时，弹着点位置会分布到目标观测范围之外，符合实际情况。

4 结论

本文在假设火箭弹的毁伤幅员是矩形区域，火箭弹在该区域内的毁伤程度均匀，目标在其区域内分布均匀的情况下，通过分析火箭弹射击存在散布误差和目标存在观测误差，利用概率方法建立了火箭弹对目标射击有效毁伤面积和火箭弹弹着点之间关系的模型，并通过遗传算法在给定单数的情况下求解出最优的弹着点位置。经过仿真实验验证，本文构建的模型对点目标和线目标同样适用，在目标观测误差较大的情况下，也可以得出符合实际情况的结果。