基于动态影响网络的空战效能评估方法

2020-05-11刘同豪

火力与指挥控制 2020年4期

潘勃，陶茜，刘同豪

（1.空军工程大学航空工程学院，西安 710038；2.西安邮电大学，西安 710161）

0 引言

作战效能评估对于研究和提高武器系统的作战效能起到了至关重要的作用，但现有的大多数效能评估分析都集中在对飞行器的效费评估和性能评估上，鲜有针对任务的作战效能评估，且其中的评估方法都存在事件关联性低、时效性差等问题，严重影响了作战效能评估的准确性。因此，作战效能评估方法必须与时俱进，引入新的评估方法和模型迫在眉睫。针对现代超视距空战系统性、动态性、不确定性等特点，可构造马尔科夫链模型，将整个作战进程分解成若干按一定概率进行状态转移的阶段性任务。目前，处理对时间依赖性和因果关系强的事件时往往采用贝叶斯网络（Bayesian Net works，BNs）的建模方法［1］。结合因果强度逻辑（Causal Strength Logic，CAST）参数的动态影响网络（Dynamic Influence Nets，DINs）更好地克服了BNs的主观性，在近些年得到了更广泛的应用［2-4］。在动态的战场环境中，海量数据的不完整性和难量化性也是进行作战效能评估亟待解决的难题，将数据进行模糊量化处理再结合层次分析法进行评估的模糊层次分析法（Fuzzy Analytic Hierarchy Process，FAHP）是解决以上难题的主要方法［5］。

综上所述，本文在应用FAHP 进行作战效能评估的基础上引入DINs，采用阶段性评估的方法，使各阶段间的行动和事件的影响性相关联，效能模型更加具有时效性和准确性，有利于C2 指控系统顺利实施，便于搜寻关键性问题和解决方案。

1 基于马尔科夫链的作战行动过程分解

马尔科夫链是一种重点重现作战过程的平面化的关系模型，其主要功能是将整个作战任务过程划分为多个不同的功能阶段，且各阶段状态之间可以利用转移概率进行关联［6-7］。马尔科夫链基本模型如图1 所示。

图1 马尔科夫链示意图

本文将作战进程分为N 个阶段，分别用［t0，t1］、［t1，t2］、…、［tn-1，tn］表示。在每个阶段所要达到的阶段效果集合表示为S={S1，S2，…，Sn}。在整个作战过程中，某个状态下的阶段效果只与其上一状态各阶段的效果值有关，即满足无后效性；针对每个阶段效果，每个状态下的效果值都是根据上一状态的效果值以一定的概率模型进行动态变化的，即满足转移概率。因此，整个作战任务可以利用马尔科夫链将其分解为多个阶段性任务进行评估研究［8］。整个作战任务所要达到的期望作战效果集合表示为D={D1，D2，…，Dn}。需要说明的是，阶段效果Si只与本阶段内行动和事件产生的效果有关，而期望效果Di则要受到之前行动和事件的影响。另外，阻碍作战任务的不可控制因素被称为事件，例如恶劣的天气和地形因素等。设可能发生在作战过程中的事件集合为E={E1，E2，…，En}。而我方根据特定的任务采取的措施则被称为行动，例如探测目标、截获目标、发射导弹等。设可能发生在作战过程中的行动集合为A={A1，A2，…，An}。

2 关于模糊层次分析模型

模糊层次分析法主要分为对指标的模糊处理和层次分析法的建模。在指标的模糊处理中，需要结合所要评估的指标建立对应规则，将模糊、不准确的要素参数化。在本文中，为简化模型计算，通过建立评分规则对参数模糊化处理。假设将指标Y 分为5 个等级，分别为很好、好、一般、差、很差，对应评分为：9、7、5、3、1［9］。

层次分析法主要用于分析影响评估结果的各因素重要程度。将各因素分为目标层、准则层和方案层3 类，对应一定的隶属关系，通过定量计算与定性分析相结合的方式确定各指标因素的权重［10］。在建立层次分析模型的过程中［11-12］，首先根据因素的隶属性质建立相应的层次结构模型。在本文中，超视距空战任务的层次结构模型如图2 所示。

参照传统标度法并对比同一层因素间的重要程度建立判断矩阵A。计算判断矩阵A 的一致性指标CI。

引入平均随机一致性指标RI，根据CI 和RI 计算随机一致性比率CR。

当CR＜0.1 时，判断矩阵A 的一致性可以接受；否则，需要调整判断矩阵A，直到其实现可以接受的一致性为止。计算判断矩阵A 的最大特征值和对应的特征向量，将特征向量归一化处理后，即为该判断矩阵A 的权向量。最后，计算组合权向量并进行组合一致性检验。下页表1 为传统1-9 标度表。

3 关于DINs 的基本模型

DINs 的基本模型如下页图3 所示。

在作战任务中，阶段效果Si往往会受到多个事件的影响。且随着时间的延续，每一个阶段效果Si对于期望效果Di的影响程度也是在不断变化的。DINs 正是对期望效果、阶段效果、事件和行动等具有因果关系的要素进行分析建模，利用条件概率等公式表示各要素随时间变化的影响值［13］。假设行动和事件对阶段效果Si的影响值为hi（xj），结合空战实际情况和专家经验，影响值往往以负指数函数衰减的形式变化。因此，设hi（xj）随时间变化的函数为f（hi（xj），t），且在初始的t0时刻影响值为hi（xj），则影响函数可表示如下，其中，αi为影响因子［14］。

表1 传统1-9 标度表

图3 DINs 基本模型图

在DINs 的模型中，建立CAST 逻辑下的概率传播方程［15］，需要计算某一时刻根节点对于子节点的条件概率P（S|x）。

其中，P（S）为前一时刻子节点的基准概率，hi（x）为正、负影响强度进行聚合后得到的整体影响值。再根据全概率公式计算P（S）在此时刻的概率。

利用基于CAST 逻辑的概率传播方程，可计算某阶段在一定的行动和事件发生的条件下，阶段效果和期望效果发生的概率，再结合式（3）进行影响值的更新，进行下一阶段效果和期望效果的计算，直至作战任务结束。

4 案例设计与仿真分析

案例背景为敌战斗机准备入侵我方空域，我方战斗机紧急升空进行拦截，敌我双方战机进行超视距空战的过程，我方的任务是消灭入侵我方领空的敌机并安全返回。按照超视距空战的实际情况，将作战任务分为战斗准备阶段、探测跟踪阶段、作战对抗阶段和退出返航阶段，它们分别对应的时间段为［t0，t1］、［t1，t2］、［t2，t3］和［t3，t4］。为完成作战任务，我方可能在作战过程中采取的行动如下。A1：地面保障；A2：战机迅速升空并进入作战状态；A3：机载雷达和地面雷达探测目标；A4：战机截获目标；A5：持续跟踪目标；A6：发射导弹并对其制导；A7：规避敌方攻击；A8：安全返回基地。阻碍我方战机完成作战任务的外界因素为事件，大致划分如下。E1：恶劣的天气和地形因素；E2：敌方进行电子干扰；E3：敌方出动飞机支援作战。

在行动和事件的共同作用下产生了不同阶段的阶段效果。S1：战斗准备效果；S2：探测跟踪效果；S3：作战对抗效果；S4：退出返航效果。

而此次作战任务的总目标即为期望效果。D：消灭敌机并安全返航。期望效果D 同阶段效果Si一样需要在每个阶段结束后进行评估，但由于之后的行动和事件还未产生，故其之后的阶段效果为0，而已产生的阶段效果对期望效果D 的影响值需要进行归一化处理。

具体的作战过程为：在S1阶段，我方采取A1、A2行动，并存在E1事件，持续时间为10 min；在S2阶段，我方采取A3、A4和A5行动，并存在事件E1和E2，持续时间为5 min；在S3阶段，我方采取A6和A7行动，并存在事件E1、E2和E3，持续时间为2 min；在S4阶段，我方采取行动A8，并存在事件E1和E3，持续时间为10 min。在某阶段内基本静态模型如图4 所示。

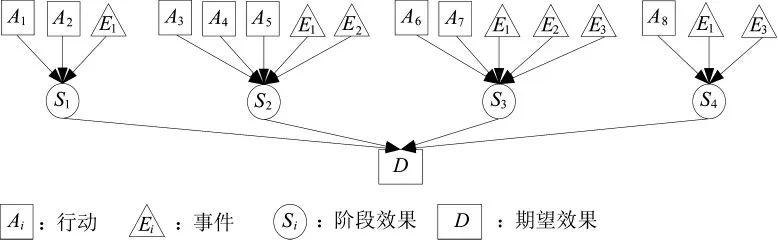
图4 基本静态模型图

假设事件对我方战斗机干扰很大，即定义为受到此事件干扰情况为很差，以此类推。我方在整个作战过程中行动完成情况和受到外部事件的干扰情况A1～A5分别为：一般、差、一般、好、差、好、一般。在执行作战行动过程中，战斗准备阶段受到干扰情况E1程度为一般；探测跟踪阶段事件中E1为差，E2为很差；作战对抗阶段事件中E1为差，E2为很差，E4为好；退出返航阶段受到事件E1为一般，E2为差。根据表1 的评分规则进行量化处理，分别得到行动和事件的量化评分情况，为A1～A8量化打分分别是：5、3、5、7、3、7、7、5。对应各作战行动阶段的过程评分：战斗准备阶段受到干扰情况下事件E1打分为5；探测跟踪阶段事件E1打分为3，E2打分为1；作战对抗阶段事件E1打分为7，E2打分为1，E3打分为7；退出返航阶段受到事件E1打分为7，E3打分为3。据图4 中DINs 的基本静态模型图，利用层次分析法建立判断矩阵。通过MATLAB 软件，检验判断矩阵一致性。得到权向量分别为D={S1，S2，S3，S4}={0.12，0.26，0.56，0.06}；S1= {A1，A2，E1}= {0.43，0.43，0.14}；S2= {A3，A4，A5，E1，E2}= {0.31，0.10，0.18，0.10，0.31}；S3={A6，A7，E1，E2}={0.22，0.22，0.06，0.12，0.38}；S4={A8，E1，E3}={0.58，0.11，0.31}。

将各权向量的值看作是事件或行动对其阶段效果影响值hi（xj）的初始值，且hi（xj）的值在该行动或事件发生的阶段不变，直至下一个评估阶段才发生值的变化。例如，在战斗准备阶段，A1、A2和E1对S1的影响值分别为0.43、0.43 和0.14，一直持续至探测跟踪阶段开始后A1、A2和E1对S1对的影响值才会随着时间变化。因此，在退出返航阶段出现的行动A8和事件E1、E3不会有影响值的改变。

结合实际作战过程和专家经验，表2 给出各行动和事件在各阶段α 影响因子的变化情况。如果事件E1、E2和E3在某一阶段出现，则用Eij表示在［tj-1，tj］阶段出现了事件Ei。

表2 α 值

在战斗准备阶段结束后即t1时刻时进行作战效能评估，得到D=S1=4.14；在探测跟踪阶段结束后即t2时刻时进行作战效能评估，得到S2=3.4。通过影响网络得出，此时A1、A2和E1对S1的影响值分别为0.36，0.57 和0.06。因此，得到D=0.32×S1+0.68×S2=3.45；同理可得到，在作战对抗阶段结束后即t2时刻时，S3=6.28，D=5.16；在退出返航阶段结束后即t3时刻时，S4=4.38，D=5.31。其阶段效果Si、期望效果D 以及采用常规层次分析法得到的效能评估结果变化如图5 所示。

图5 评估结果示意图

从图中对比阶段效果Si和期望效果D 的评估结果不难发现，在作战对抗阶段，阶段效果值比期望效果值高出不少。经数据分析，发现我方战斗机在此阶段较好地完成了发射导弹并对其制导以及规避敌方攻击的行动，并且外部事件没有对我方行动造成太大阻碍，使我方顺利完成了此阶段的任务；但由于在前期探测跟踪阶段，我方受到了敌方强烈的电子干扰导致探测、截获和跟踪目标较差，探测跟踪效果不佳，最终影响到了下一阶段的总体效果。并且我方战斗机在作战对抗阶段的出色表现持续影响到了退出返航阶段，并进一步提高了退出返航后期望效果的评估值。而采用常规层次分析法所得到的效能评估值，无法反应体现各作战阶段中各行动的完成情况和事件的干扰情况，难以实现实时评估的功能。通过对比分析可以发现，结合动态影响网络建立的期望效果曲线不仅在评估结果上更加客观公正，而且能更好地反映执行作战任务过程中作战效能的变化。