采用有限元方法的舵系受力直接计算

王鹏印 王海波 沈会宇 王运才 杨志宏

（大连船舶重工集团设计研究院 大连116021）

引 言

船级社规范规定了船体结构强度、重要机械尺寸、所有材料质量、各系统完整性以及其他特征或辅助系统的功能等，旨在控制船舶的安全与质量满足一定的要求，以保证船舶具有良好的适航状态。本集团所建船舶主要采用LR 规范、DNV 规范和CCS 规范等。LR 及DNV 规范是当今世界上应用最为广泛的船级社规范之一，而中国CCS 船级社规范近些年在国内被普遍应用，因此下文中将主要对上述三个船级社规范进行分析研究。

船舶规范中有很多数据因无法精确定量计算而采用经验公式。这些经验公式一般由拟合得到，没有完整的理论推导过程，经验公式更趋向于实际应用，因此在理论技术尚未成熟或有限元计算尚未应用的过去得到了大规模的应用。相关船级社一直允许采用直接计算法计算舵杆弯矩（Mb），DNV 还提供过直接计算法的指导文件，但需要的计算参数很多、计算过程很复杂。直接计算可以利用公式手算，也可以利用有限元软件计算。在有限元理论及有限元计算大规模应用的今天，规范中很多原来用经验公式计算得出的结果均被要求采用直接法计算。因此，有限元计算方法增加了一种新的舵系受力直接计算方法，对指导船舶设计乃至日后的发展方向都起到了重要的作用。

舵系是船舶的转向操控系统，舵机输出的扭矩通过舵杆传递到舵叶上，螺旋桨推力作用于舵叶上产生力矩使船舶转向，因此舵系结构中舵杆的稳定工作是保证船舶安全稳定运行的前提。而舵杆弯矩是设计舵杆的重要参数，其决定了舵杆的直径并间接决定了舵叶的厚度。因此该文在舵杆直径计算的基础上，针对规范中舵杆弯矩的经验公式以及用有限元方法计算进行了对比和分析。为便于从数值上更加直观地对比，该文依托某大型散货船进行分析。

1 某大型散货船基本参数

某大型散货船船长292 m、型宽45 m、型深24.8 m、主机型号MAN B&W 6G70ME-C9.2、主机最大功率15 360 kW×69.6 r/min、设计航速15.75 kn、舵叶面积77.07 m2。

2 LR 规范中舵杆弯矩的计算方法

关于舵杆弯矩，LR 规范原则上建议在进行舵杆直径计算时采用直接法计算舵杆弯矩。在工程领域中，直接计算法即采用有限元理论直接得出所需数值的方法。若船舶设计单位无法进行直接计算，LR 规范也根据实际情况给出了如下经验公式［1］：

舵杆弯矩：

式中：舵叶平均高度hR= 12.2 m；

舵叶平均宽度c= 6.317 m；

舵叶面积A= 77.07 m2；

舵叶受力CR= 3 383 297 N。舵杆直径：

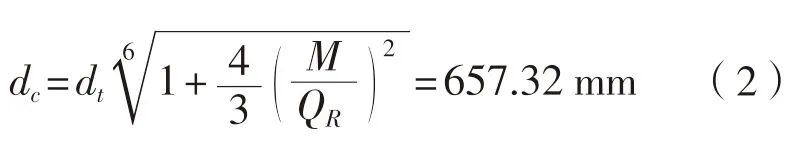
式中：舵柄处舵杆直径dt= 546.14 m；

舵杆扭矩QR= 2 198 715 N·m。

综上所述，用LR 提供的经验公式计算得出：上舵钮处舵杆所受弯矩2 719 kN·m，上舵钮处舵杆直径为657.32 mm。

3 DNV 规范中舵杆弯矩的计算方法

关于舵杆弯矩，DNV 船级社同样推荐采用直接计算法计算，但考虑到船舶设计院所的计算能力，DNV 船级社在规范中也同样给出了一个舵杆弯矩计算的经验公式［2］。但此经验公式较LR 经验公式有较大不同。

舵杆弯矩：

式中：舵叶受力FR= 3 383 297 N；

舵叶平均高度H= 12.2 m。

舵杆直径：

式中：舵柄处舵杆直径dt= 546.14 m；

舵杆扭矩QR= 2 198 715 N·m。

综上所述，用DNV 船级社提供的经验公式计算，上舵钮处舵杆所受弯矩2 428 kN·m，上舵钮处舵杆直径为641.48 mm。

4 CCS 规范中舵杆弯矩的计算方法

关于舵杆弯矩，CCS 规范没有像DNV 和LR规范中给出了计算舵杆弯矩的经验公式［3］，只是将舵杆弯矩定义为“剖面的舵杆弯矩”，具体计算方法没有任何描述。而CCS 规范舵杆直径计算公式同DNV 和LR 规范的公式完全相同，对设计经验欠缺者，尤其是既没有掌握其他规范诸如DNV和LR 的经验公式计算法，又没有掌握有限元理论的直接计算法，因此舵杆弯矩计算对于采用CCS规范设计的人员来说是一项不小的挑战。

5 有限元模拟软件计算舵杆弯矩

关于舵杆弯矩，CCS 规范中没有给出可参考的经验计算公式，虽然DNV 规范和LR 规范分别给出了不同的经验公式，但DNV 和LR 规范中已明确推荐首选应用有限元理论的直接计算法。而且所谓的经验公式都是在前人的经验上总结而来，没有完善的理论推导，正因为其没有完善的理论作指导，所以在公式制定时都预留了很大的安全余量，无形之中浪费了很多材料。

本文将分别使用建模软件Solidworks［4］和有限元计算分析软件Hyperworks［5］依托某大型散货船对半铲形舵直舵杆的上舵钮处弯矩进行有限元分析计算。首先用Solidworks 软件分别建立舵系零件模型并装配成整体；然后将装配体模型导入到Hyperworks 软件中进行力学分析；最后对用有限元理论计算的结果进行分析总结。

5.1 Solidworks模型建立

Solidworks 是功能强大的三维CAD 设计软件，具有高效的实体建模功能。因此该文用Solidworks软件按1：1 的比例对舵叶、舵杆、舵销、上下铸件、挂舵臂、螺母等零件进行精确的三维建模。

图1 舵系装配体模型

虽然计算目的是求得舵杆弯矩，但有限元软件计算是对整体进行计算，因此需要把分拆的零件组合成装配体。装配体需要做间隙、干涉等检查。三维模型的质量对后期的网格划分及计算精度都有很大影响，所以在模型建立时需要核对每一个尺寸，确保准确无误。该文数据依托于某大型散货船，舵系装配体模型见图1。

5.2 Hyperworks力学分析

Hyperworks 是一个创新、开放的企业级CAE平台，它集成了设计与分析所需的各种工具，具有强大的几何清理和网格划分等功能，能够对模型进行高效的力学分析，因此该文选用hyperworks 对模型进行力学分析。

5.2.1 在Hyperworks 中建立有限元模型

（1）载入Optistruct 用户界面并导入模型文件；

（2）定义弹性模量、泊松比等材料属性和几何属性；

（3）采用四面体单元对模型进行网格划分，详见图2。

图2 有限元模型网格划分

5.2.2 施加载荷并设定边界条件

（1）创建载荷集：将规范中计算出的舵力均匀分布到舵叶的每个节点上；对舵叶上的节点施加Z方向的载荷，详见图3。

图3 舵叶均布载荷分布

（2）创建约束：对舵杆和挂舵臂上表面施加固定约束，上舵承处施加X、Z方向约束，Y方向自由，参见图4。

（3）创建Optistruct 的载荷工况。

图4 舵叶模型约束

5.2.3 Hyperworks 求解

Optistruct 是以有限元理论方法为基础的结构优化计算工具，运行该程序求解后即可在相应图框内查看所需结果。

5.2.4 在Hyperview 中查看结果并进行后处理

（1）舵叶位移云图，见图5。

图5 舵系位移云图

（2）舵叶形变云图，见图6。

图6 舵系形变云图

（3）舵杆弯矩计算所需数值结果。

F1= 12 386 N，为舵杆上表面处约束节点力之和；

F2= -273 990 N，为舵杆上舵承处约束节点力之和；

L1= 8 372.5 mm，为舵杆上表面到下舵承中心处的距离；

L2= 6 162.5 mm，为上舵承中心到下舵承中心处的距离。

5.3 有限元计算结果分析说明

5.3.1 初步计算结果

（1）上舵钮处舵杆弯矩

（2）舵叶最大位移

δ= 68.39 mm。由位移云图可以看到舵叶尾部下端为最大位移处，然后逐渐上移，直到舵叶上铸件处位移基本为0。

（3）舵叶受力初步分析

从计算结果可以看出，挂舵臂承担了部分应力，说明挂舵臂刚度变化对舵杆受力产生重要影响，挂舵臂刚度越大，舵杆下舵承处的弯矩越小。

5.3.2 模型简化处理

舵系中的一些结构给模型的网格划分造成很大困难，而忽略这些结构或用相似的结构代替对有限元计算的结果不会造成太大影响，且很大程度上简化了计算难度。因此，文中对舵系模型作了一定的假设和近似处理：

（1）由于考虑到螺纹结构会给模型的网格划分造成不必要的麻烦，因此所建模型中会以圆柱体代替螺纹，但直径保持不变；

（2）由于倒角特征会给模型的网格划分及后期计算增加很大难度，而忽略倒角后对计算结果的影响不大，因此模型中无倒角；

（3）由于舵叶所受重力与浮力均为垂向力，舵系重量由舵承担，重力对舵力影响可忽略不计，因此计算时可忽略重量的影响。

6 舵杆弯矩规范计算和有限元计算结果对比分析

6.1 DNV规范和LR规范计算舵杆弯矩和直径

（1）DNV 规范计算舵杆弯矩和舵杆直径

舵杆弯矩：Mb= 2 428 kN·m ；

舵杆直径：dc= 641.48 mm；

（2）LR 规范计算舵杆弯矩和舵杆直径

舵杆弯矩：Mb= 2 719 kN·m ；

舵杆直径：dc= 657.32 mm。

6.2 有限元软件计算舵杆弯矩和直径

用Solidworks 软件精确建立舵系模型，导入Hyperworks 后用有限元理论方法进行直接计算。有限元方法不仅有较高的计算精度，而且能够适应各种复杂的形状，保证了计算结果的准确。

舵杆弯矩：Mb= 1 580 kN·m ；

舵杆直径：dc= 595.97 mm 。

6.3 规范法和有限元法计算结果分析

LR 规范和DNV 规范的舵杆弯矩为经验公式，为保证所设计产品的质量，经验公式通常都预留有很大的安全余量。DNV 也有直接计算规范，虽然计算结果更准确，但相对复杂繁琐。由表1 可见，以LR 规范为衡量基准，有限元方法计算的舵杆弯矩为LR 规范的58%，舵杆直径为LR 规范的91%，此趋势间接证明了有限元计算方法的可行性。有限元方法的计算结论需要船级社认可，其为舵系分析提供了另一种计算方法。

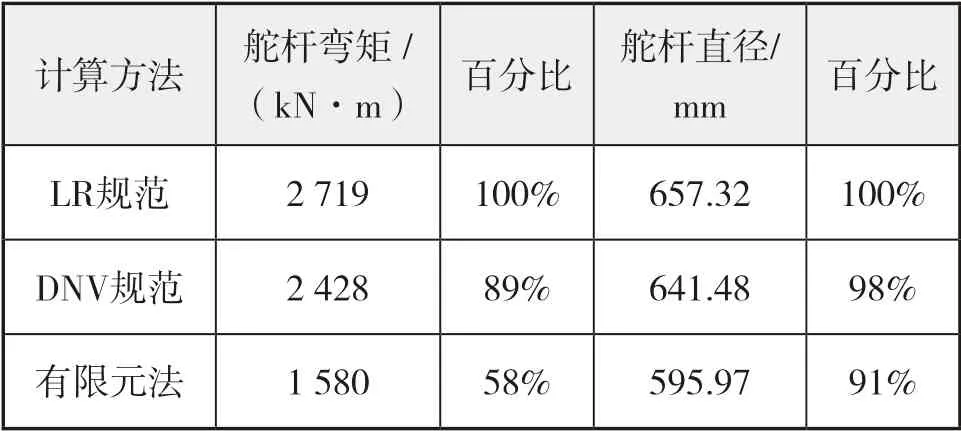
表1 规范法和有限元法计算舵杆弯矩和直径

7 结 语

该文研究的舵杆弯矩用船级社规范和有限元理论分别进行了计算。在参阅大量规范、规则和文献的基础上，分别用DNV 规范和LR 规范计算舵杆弯矩；然后再对舵系装配体模型用Solidworks软件进行合理简化；其次用有限元分析软件Hyperworks 对舵系装配体进行直接计算，得到舵杆弯矩值；最后将规范计算值和有限元计算值进行对比分析。

该文计算数据依托于某大型散货船，分别用规范法和有限元法对舵杆弯矩进行对比分析。结果表明，有限元方法计算的舵杆扭矩为规范法的58%，舵杆直径为规范法的91%。规范法采用经验公式计算，有限元法是应用软件直接计算，考虑到舵系是保证船舶安全稳定运行的重要设备，因此无论采用哪种方法均需要预留一定的安全裕度。有限元方法计算舵系受力是对规范经验公式计算方法的一个补充，为两个方法之间的相互校核提供了可能。