基于FLUENT 的过滤器滤网流场模拟计算

侯宗宗 郭雨菲

（中船重工第七二五研究所 洛阳471023）

引 言

随着航运业环境保护要求越来越严格，尤其是船舶压载水的处理更为重要，而滤网作为船舶压载水自动反冲洗过滤器的重要部件之一，直接决定过滤器的处理水量、过滤效率等工作性能，其结构采用四层金属丝网烧结而成，属于多孔材料使用范畴，具有结构强度好、耐磨与耐腐蚀等优点［1］，并有较好的流体渗透性能［2］。滤网的流场特性，主要涉及在工况中的压力损失、过滤流速及湍流情况。滤网内部的流动状况对于金属丝网的选型与设计，优化滤网的性能可使过滤器达到过滤效果强、使用周期长等目的［3］。目前，采用各种现场试验来研究与分析滤网的主要流阻性能参数［4］，即在不同的流速及各层丝网结构组合的条件下获得滤网的流场性能参数，并进一步改变相关设计条件取得相对达到设计要求的滤网结构，这将导致研发时间太长，且属于反复性的组合试验，更盲目与费力。

为解决上述问题，并省去大量重复性的组合试验，本研究过滤器的滤网为四层烧结不锈钢金属丝网，采用三维软件构建了滤网三维实体模型，依据船舶压载水过滤器在试验平台的过流试验来模拟计算其内部流场情况［5］，采用基于CFD 方法对其性能进行计算，能够全面呈现滤网内部的流场特性，包括速度场、压力场、湍流分布等，并获取滤网的流速-压差曲线以及拟合方程，为滤网的性能预报提供研究方法，并为进一步改善过滤器性能、延长使用周期提供依据。

1 理论方程和计算模型

1.1 理论方程

本文滤网流域模型是在三维定常的计算条件下，不可压缩的湍流流动，则流场的连续性方程和动量方程（N-S 方程）［6-8］：

采用标准的k-ε湍流模型（standardk-εmodel）：

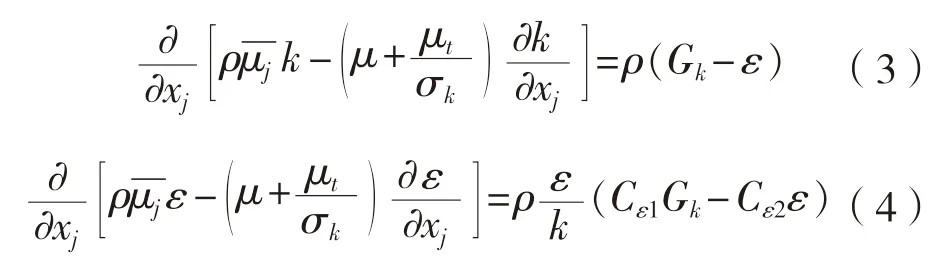
其中涡粘性系数用μt表示：

式中：xi和xj分别为i和j方向上的位置坐标；ui与uj均为瞬时速度，m/s；t为时间，s；p为静压，Pa；ρ为流体密度，kg/m3；gi为单位质量的重力，m/s2；ε为耗散率；µ为动力粘性系数，Pa·s；为雷诺应力张量；Gk为因平均速度梯度而产生的湍动能生成项，J。

同时，上述方程中的附加经验常数值为：

1.2 网格划分

选取的过滤器滤网采用四层烧结金属丝网，见图1，骨架层为孔板结构，依据实际编织情况建立其三维实体模型，见图2。基于CFD 软件构建滤网的外流场区域，见图3，模型采用非结构网格划分［7］，适当优化网格质量，并有效地控制计算量［8］，滤网流域模型网格总数为37 839 153，见图4。

图1 四层烧结金属丝网

图4 滤网流域网格划分

保证来流均匀以及出口不受湍流的影响，在滤网流域的前后均适当延长。

1.3 边界条件

将滤网流域四周的壁面设置为周期性无滑移［6-8］，近壁面区域的函数选择标准壁面。进口设成速度入口，出口设成一个大气压的压力出口。在迭代求解上，压力和速度耦合计算采用SIMPLE 算法，定常状态，压力插值采用标准格式，其余设置则选择默认值，并考虑收敛情况，选择适当的迭代步长。

2 计算结果及分析

2.1 流速-压差曲线

通过在不同的来流流速情况下，对其条件下的流场进行计算，得到了相应的仿真计算压差值，而其试验值是由整机SRF-100V 过滤器在过流试验平台实测，过滤器进出口管径为DN80，滤网直径245 mm，长为513 mm，采用水泵安全试验流量范围为70 m3/h 至100 m3/h，换算滤网处流速为0.365 m/s 至0.521 m/s。以模拟值与试验值绘出其性能曲线，见图5，仿真模拟结果与试验值相比，可以得出相对贴合度较高，走势基本一致。而过滤器的实际试验条件比较复杂，受到取压口位置、仪表精确度等不确定因素较多。结果表明：试验值与模拟值相差最大为9.7%；流速的增大会使湍流更为激烈，且损失增多，导致其压差值也增大；按照滤网流速与压差值的关系获得其拟合方程为：ΔP= 5 519.3v2 + 2 237.9v，拟合相关性为99%；三维实体仿真模拟结果具有较高可信度，并可以较全面呈现其流动性能。

2.2 流场特性分析

选取以设计流速为0.5 m/s 的速度进入滤网流域。由图6 和图7 可知滤网流场内部的压力分布与速度分布情况。

图5 流速-压差曲线

图6 截面压力分布图

图7 截面速度分布图

由于滤网内的丝网编织结构紧凑，流道非常不规则，水流先冲击保护网，经主滤网时流道变窄，使得压力分布比较集中，出现明显的压降，在流经滤网流体区域后总压值有明显的减小，而在滤网附近因为丝网密实使得水流在此处产生激流，在孔板过后表现较为明显的尾流形状，这与实际情况相符合。

下页图8 展示出压力沿轴向方向的分布情况，能直观反映出压力的变化情况，因滤网编织烧结会造成压力波动而引起压力更大的损失，证明了滤网的流阻特性。图9 展示了速度沿轴向方向的分布，进一步证实了上述的激流情况并因能量损耗而致使过后流速有所降低，在滤网之后趋于稳定。图10为主滤网处截面压力分布图，因四层丝网更为密实，贴近孔板处容易出现激流情况而致使在孔板区域出现明显的压降区域；图11 为孔板截面速度分布图，孔中心速度较大，符合实际情况。由湍流动能图（图12）能够得出滤网对流体流域的湍流影响最大，主滤网区域处湍流更为激烈，特别是主滤网前的流域，呈现出非常鲜明的湍流区域，但水流之后一段距离，湍流强度也随之逐步降低；图13 显示滤网流域内部的流线状况，更清晰地分析滤网内部流动，在孔板处呈现激流并在其后产生明显的涡流。

图8 压力沿轴线方向的分布图

图9 速度沿轴线方向的分布图

图10 主滤网处截面压力分布图

图11 孔板处截面速度分布图

图12 截面湍流强度分布云图

图13 滤网流线分布情况

3 结 论

本文采用基于FLUENT 的滤网流场数值模拟方法，分别建立与分析了滤网四层烧结金属丝网三维实体模型下的流场性能情况，包括速度场、压力场、湍流强度等情况。基于不可压缩的湍流理论获得总压值，通过在不同进速条件下滤网流场的模拟值与试验值对比，可得出以下结论：

（1）基于CFD 理论计算得到的模拟结果值和试验压差值相差不大，而且流速-压差的基本趋势相同，证明了数值模拟研究方法的可信度，并获得其拟合计算方程，为有效地研究与分析滤网的压降、流速等各方面的性能；

（2）在0.5 m/s 水流的计算条件下，最大流速可达到3 m/s，压差值为2 436 Pa，与试验值相差9.7%，符合实际情况；滤网的压损随着进速流速的增大而变大； 滤网内部丝网密实，水流流速越大，会造成更多的压力损失，并在滤网前后区域呈现明显的压降；在骨架层孔板的圆孔处激流情况更为突出，主滤网区域的湍流强度较强，其压力损失也主要集中于孔板圆孔区域，符合实际情况。