含分流电路Galfenol声子晶体的带隙与减振性能

2020-05-10曹淑瑛王金川郑加驹张福宝

压电与声光 2020年2期

曹淑瑛，王金川,郑加驹,张福宝

(1.河北工业大学省部共建电工装备可靠性与智能化国家重点实验室，天津 300130; 2.河北工业大学河北省电磁场与电器可靠性重点实验室，天津 300130)

0 引言

与传统声子晶体相比，含分流电路的压电声子晶体[1-4]可通过调整分流电阻、电感和电容等元件对其布喇格带隙(BBG)和共振带隙(RBG)调节，以降低振动传输。该减振控制法有望克服主动控制系统庞大且需能量供给的缺陷，在减振控制中有良好的应用前景。但压电智能材料存在易老化、工作温度范围窄及过热失效等缺点，限制了其应用。

与压电材料相比，磁致伸缩智能材料(如Terfenol-D和Galfenol)[5-7]有工作温度范围广，稳定性好及能量密度高等特点，在驱动[7-8]、分流阻尼[9-10]、振动能量采集[6]和声子晶体[11-16]等器件中有潜在的应用前景。然而，该器件显示了磁-机-电耦合非线性[5-6]，这给器件的设计和性能预估带来困难。

目前，已有研究利用等效压磁材料模型[11-13]、一维[14]和二维[15-16]Z-L模型来描述Terfenol-D的磁-机耦合非线性，并用平面波展开法分析其声子晶体的BBG。Matar等[11-12]和Zhou等[13]表明，在外部静磁场作用下，二维Terfenol-D声子晶体内的Terfenol-D因磁致伸缩效应产生了机械形变和弹性模量变化，从而使其BBG产生明显变化，且外加磁场方向对BBG的宽度和位置有显著影响。Ding等[14]和Zhang等[15]表明，Terfenol-D声子晶体的BBG除受外加磁场和预应力影响外，也受器件几何参数的影响。Gu等[16]表明，磁场和预应力可使Terfenol-D声子晶体的BBG获得新的点缺陷模态。以上均是利用材料的磁致伸缩效应对其BBG调控的研究。如何利用材料的逆磁致伸缩效应，将有害的振动能转化为电能，并通过分流元件调整其带隙，实现有效减振的研究还未见报道。

本文考虑Galfenol材料磁-机-电耦合的逆磁致伸缩非线性，利用Armstrong模型确定了材料特性参数，推导和验证了在分流电路下材料的有效弹性模量，并采用所建立的一维Galfenol声子晶体振动模型对其在不同偏置磁场Hb、应力σ及分流电容Cs下的带隙调控法及减振性能做了深入研究。

1 含分流电路Galfenol声子晶体理论建模

将Galfenol棒紧密缠绕螺旋线圈，通过线圈与分流电路相连，并将该Galfenol棒周期性地连接到环氧树脂棒上，形成在x方向上交替排列无限一维声子晶体结构，如图1所示。图中，P和Q段分别为长度lm的Galfenol棒和长度lb的环氧树脂棒，a=lb+lm为晶格常数，周期n=1,2,3,…,v(v为周期总数)，Zs为分流阻抗。该声子晶体第v个周期Q段右边界是自由的，当其第1个周期P段左边界受位移激励幅值Yejωt(ω为激励角频率)激励时，由逆磁致伸缩效应和法拉第定律可知，P段中磁感应强度B发生变化，从而匝数N和长度lc的线圈产生感应电压u、电流i和磁场Hc=Ni/lc，随之P段有效弹性模量Ee会变化，从而实现其弹性波调控。

图1 含分流电路的一维Galfenol声子晶体结构

Galfenol声子晶体的理论建模基于以下假设：

1) Galfenol中沿x轴的磁场H、B分布均匀。

2) 沿x轴的应变ε和σ处处相等。

3) 螺旋线圈的lc和横截面积Ac分别与Galfenol棒的lm和横截面积Am相同。

1.1 磁致伸缩材料本构方程

Armstrong模型[5]能准确描述Galfenol磁致伸缩效应和逆磁致伸缩效应的磁-机耦合非线性行为，并可描述该材料参数(如弹性模量、压磁系数、磁导率)随应力与磁场变化的非线性特性。

图1中，沿x轴给Galfenol棒施加H和σ时，材料的本构方程为

ε=σ/Em+d1H

(1)

B=d2σ+μ0μrH

(2)

式中：μ0为真空磁导率；d1为磁机转换耦合压磁系数；d2为机磁转换耦合压磁系数；Em为弹性模量；μr为相对磁导率。参数d1、d2、Em、μr均随磁场与应力变化，可由Armstrong模型表示为

(3)

(4)

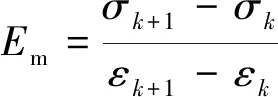
(6)

(7)

(8)

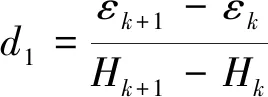
(9)

式中：α1=sinθcosφ；α2=sinθsinφ；φ为方位角；θ为极角；Et为总能量；Ms、λ100、Es、K分别为材料的饱和磁化强度、饱和磁致伸缩、饱和弹性模量和各向异性常数；γ、Ω为材料的两个因子；k和k+1为B、H、ε或σ的连续值。

Galfenol中，H=Hb+Hc。在Yejωt激励下，Galfenol产生的i很小[6]，从而Hc≪Hb，因此，可认为Galfenol在H≈Hb和σ附近工作，可利用式(3)～(9)计算该工作点(Hb,σ)下的材料参数。

1.2 分流电路下有效弹性模量

在Yejωt激励下，基于假设1)、2)和法拉第定律可得线圈中产生的感应电压为

u=-NAcBs

(10)

式中s=jω为拉普拉斯算子。

将式(2)和H=Hb+Hc代入式(10)，并考虑线圈的电阻Rc和Zs，可得：

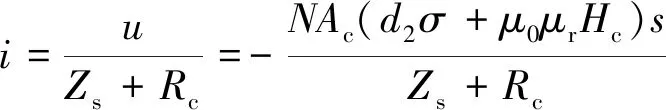
(11)

由式(11)和Hc=Ni/lc可求得Hc，并将其代入式(1)可得：

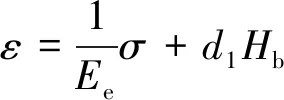
(12)

其中：

(13)

式中：Lc=μ0μrN2Ac/lc为电感；κ=[d1d2Em/(μ0μr)]1/2为磁机耦合因子。

由式(13)可得归一化有效弹性模量为

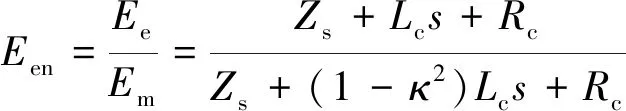
(14)

将复数Ee和Een表示为实部和虚部的形式为

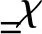
(15)

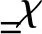
(16)

图1中，Zs=1/(Css)时，器件的电固有频率fn为

(17)

式中Cs为分流电容。

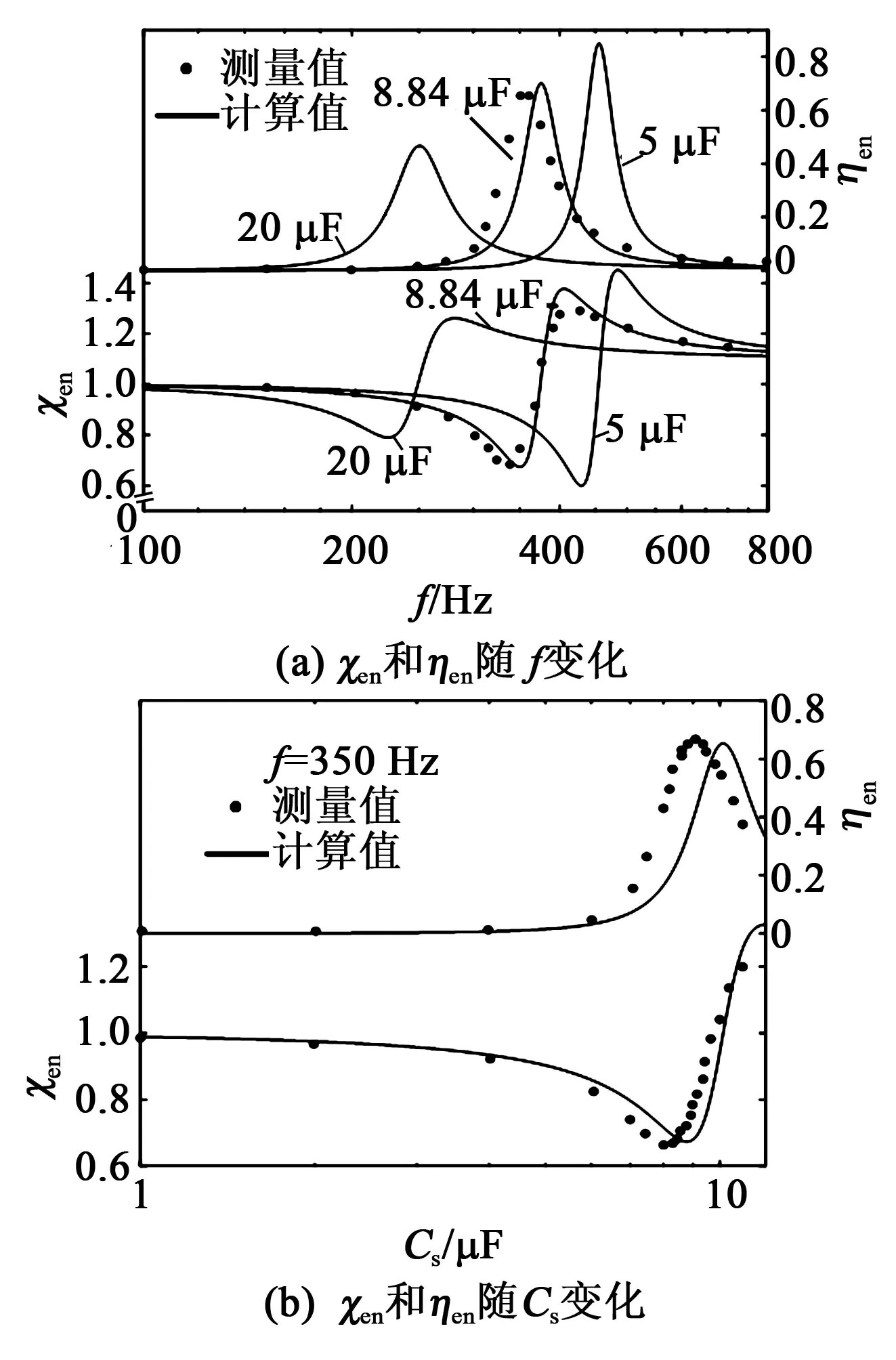
图2 Galfenol归一化的储存刚度和损耗因子特性曲线

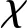
比较图2(a)、(b)中计算和实验曲线可知，计算曲线与实验曲线吻合良好，这说明式(14)可提供Een随f和Cs的合理数据趋势。

1.3 振动模型与传递矩阵理论

图1中，一维声子晶体的纵向振动方程[2]为

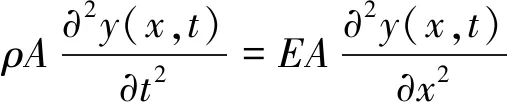
(18)

式中：y(x,t)为在x处的位移；ρ为密度；A为横截面积；E为弹性模量。对于P段，Galfenol棒的密度、横截面积和弹性模量分别为ρm、Am和Ee。对于Q段，环氧树脂棒的密度、横截面积和弹性模量分别为ρb、Ab和Eb。

利用Bloch定理和传递矩阵方法，可推得式(18)的特征值方程[2]为

|T-eα+jβI|=0

(19)

图1中，当该声子晶体第1个周期P段左边界受Yejωt激励时，利用边界条件和传递矩阵法[2]，可得其第v个周期Q段右边界位移幅值yvQ(va)与第1个周期P段左边界位移幅值y1P(0)的比，即位移传输为

(20)

式中D=[cos(λ2a) sin(λ2a)]，λ2=(ρb/Eb)0.5ω为Q段的波数；Tv为T的v次方。

2 结果与讨论

图1中，环氧树脂棒和Galfenol棒有相同的直径db=dm=5 mm和lb=lm=35 mm；N=460和内阻Rc=6.99 Ω；环氧树脂的Eb=4.35 GPa，ρb=1 180 kg/m3[2]；Galfenol的Es=59 GPa，Ms=1.66/μ0A/m，λ100=212×10-6，K=1.75×104J/m3，ρm=7 496 kg/m3，γ=0.9和Ω=707[5]。利用上述参数，采用所建的模型计算所得曲线如图3～5所示。

图3 Hb不同时，Galfenol参数随应力变化曲线

图4 开路下Galfenol声子晶体的性能曲线

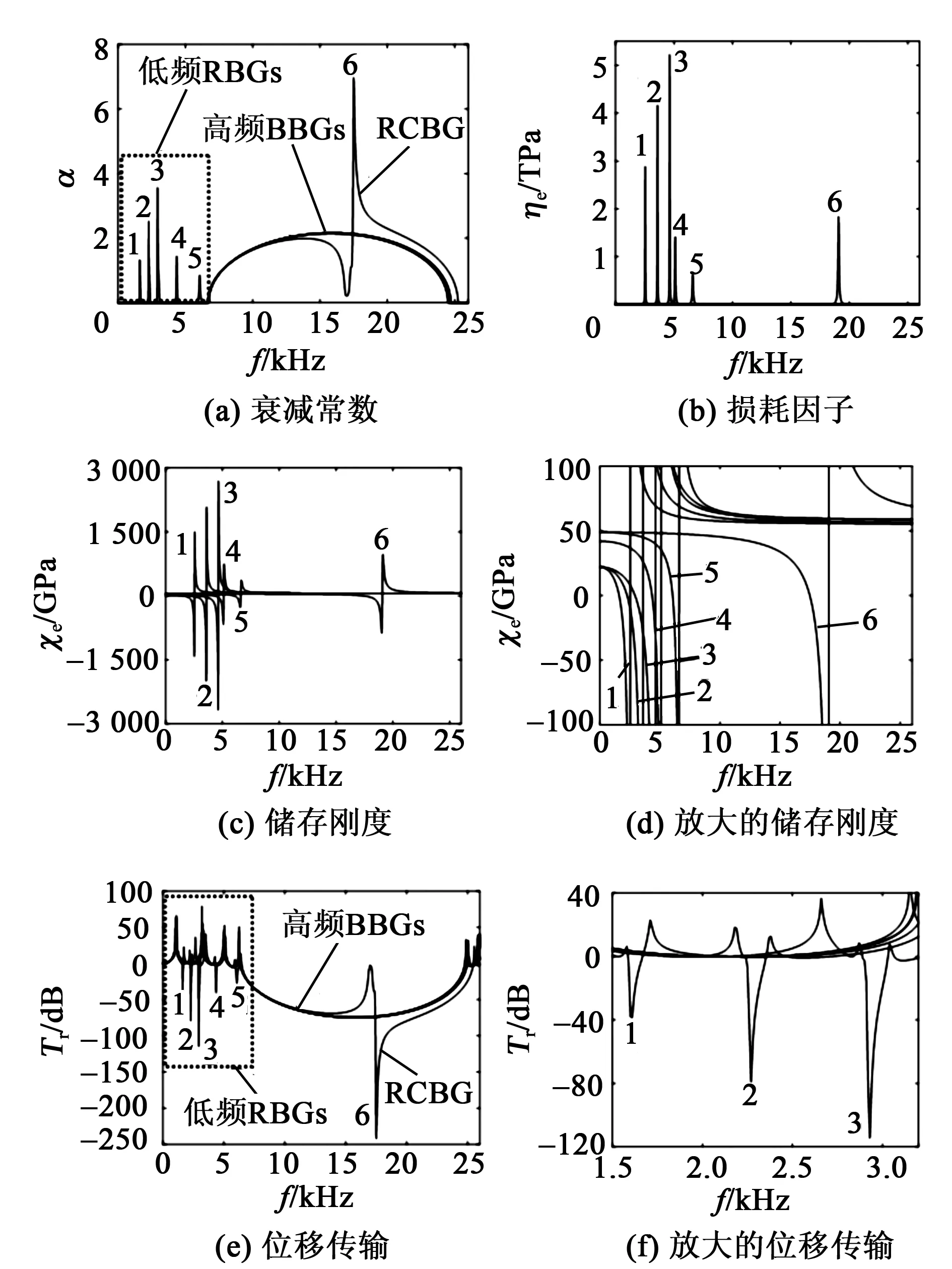
图5 分流电容电路下Galfenol声子晶体的性能曲线

2.1 Galfenol特性参数的非线性

图3为利用Armstrong模型计算在不同磁场下Galfenol参数Em、d1、d2、μr、Lc和κ随应力变化的非线性曲线。由图可看出，对于给定的H=Hb，Em首先随着σ的增加先减小后增加，最后接近Es=59 GPa。而d1、d2、μr、Lc和κ随着σ的增加先增加后减小。由于Galfenol棒的滞后小，故图3(c)中d1≈d2，这符合热力学理论。此外，在点(1.78 kA/m,-8.7 MPa)处，Lc和κ达到最大，即Lc max=98.9 mH，κmax=0.777。

比较图3中计算曲线与测量曲线[5]发现，计算和测量的d2-σ、Em-σ曲线有近似的数量和趋势，且在(H,σ)处，计算d1-σ、μr-σ与测量d1-H、μr-H[5]曲线的d1、μr数值非常近似。结果表明，Armstrong模型能准确描述Galfenol参数非线性特性。

在Hb=1.78 kA/m和σ=[-25 MPa，0]下，参数Em、d1、d2、μr、Lc和κ的数值变化范围最大，这有益器件应用。

2.2 开路下Galfenol声子晶体的性能

图4为在开路(即Zs=∞)下，σ和H=Hb对Galfenol声子晶体BBGs的影响。由图4(a)可看出，在H=Hb=1.78 kA/m时，BBGs的起始频率fs≈6.58 kHz几乎不随σ变化，而αp和fc随σ变化显著。

不同H=Hb下，αp-σ和fc-σ曲线如图4(b)所示。显然，对于给定的Hb，αp、fc随σ的变化规律与图3(a)所示的Em随σ的变化规律一致。这是因为当Zs=∞时，由式(13)可知，Ee=Em。即当Zs=∞时，BBGs特性仅取决于Em。此外，当Em接近Es(Es=59 GPa)时，BBGs的αp和fc数值分别接近最大值(αpmax=2.19,fcmax=24.66 kHz)。

实际应用中，为了实现减振，常希望在施加的Hb和σ较小时，器件的αp和fc可接近αpmax和fcmax，从而实现最佳或次最佳减振。由图4(b)可看出，在1.78 kA/m和-25 MPa下，器件的αp=αpmax,fc=fcmax,因此，(1.78 kA/m,-25 MPa)为器件的最佳工作点。此外，在工作点(1.78 kA/m,0)处，器件的αp≈2.13,fc≈23.99 kHz,分别接近αpmax=2.19和fcmax=24.66 kHz，因此,该点为次最佳工作点。

2.3 分流电容电路下Galfenol声子晶体的性能

图5为Zs=1/(Css)下,Hb=1.78 kA/m、不同σ和Cs时Galfenol声子晶体的性能。图中，曲线1：σ=-8.7 MPa，Cs=0.1 μF；曲线2：σ=-8.7 MPa，Cs=0.05 μF；曲线3：σ=-8.7 MPa，Cs=0.03 μF；曲线4：σ=-2 MPa，Cs=0.05 μF；曲线5：σ=0，Cs=0.05 μF；曲线6：σ=0，Cs=0.006 μF。对于给定的Hb=1.78 kA/m和σ=0、-2 MPa、-8.7 MPa，可由图3(a)、(d)得到其相应参数：Em分别为48.8 MPa、41.9 MPa、21.9 GPa，Lc分别为13.8 mH、26.8 mH、98.9 mH，κ分别为0.339、0.526、0.777。因此，图5中的曲线1～3和曲线5、6显示了变化的Cs对器件性能的影响，而曲线2、4和曲线5显示了变化的Lc、κ和Em对器件性能的影响。由图5可得：

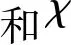
2) 当Cs和器件内在Lc组成的电磁振荡器起作用时，该声子晶体不仅有BBG，且有RBG和共振公共带隙(RCBG)。

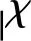
然而，曲线1～5的高频BBGs几乎不随Cs和σ变化，且与开路下最佳BBG具有相同的起始频率(fs≈6.58 kHz)、最大衰减常数峰值(αpmax≈2.19)和最大截止频率(fcmax≈24.66 kHz)。这是因为，由图5(c)、(d)可知，在谐振窄频带RBGs后，Ee总是迅速下降到饱和弹性模量(Es=59 GPa)。

此外，图5(a)、(e)表明，Cs=0.006 μF，σ=0时，RBG进入BBG，两带隙合并产生了衰减幅度很大的RCBG。

3) 比较图5(a)、(e)可知，图5(a)中衰减常数大的频率区域与图5(e)中振动衰减幅值大的频率区域相对应。此外，图5(e)表明，在f=6.58～24.66 kHz内，BBGs和RCBG的振动衰减幅值分别可达80 dB和250 dB。图5(e)、(f)表明，曲线1～3相应的3个RBGs振动衰减幅值分别约达40 dB、80 dB和120 dB，但其频率范围很窄，分别为1.58～1.66 kHz，2.24～2.35 kHz和2.88～3.04 kHz。为了改善RBGs带宽，需研究其混合分流电路[2]和非线性分流电路[4]。