An explicit representation and computation for the outer inverse
2020-05-10ShengXingpingChenJianlong
Sheng Xingping Chen Jianlong
(1School of Mathematics, Southeast University, Nanjing 211189, China)(2School of Mathematics and Statistics, Fuyang Normal University, Fuyang 236037, China)
Abstract:First, an explicit representation for a matrix A∈Cm×n with the prescribed range T and null space S is derived, which is simpler than is proposed and investigated. Then, the computational complexity of the introduced algorithm is also analyzed in detail. Finally, two numerical examples are shown to illustrate that this method is correct.
Key words:outer inverse; explicit representation; elementary operation; computational complexity

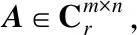

The {2} -inverse plays an important role in a stable approximation of ill-posed problems and in linear and nonlinear problems involving a rank-deficient generalized inverse[2-3]. In particular, {2} -inverse can be used in the iterative methods for solving nonlinear equations[1,4]and in statistics[5-6].


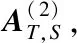
ind(AG)=ind(GA)=1
(1)
Furthermore, we have
(2)
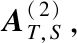
Lemma2[17]LetA,T,SandGbe the same as those in Lemma 1. LetVandU*be matrices whose columns form the bases ofN(GA) andN((GA)*), respectively. DefineE=VU. Then,Eis nonsingular, satisfying
R(E)=R(V)=R(GA),N(E)=N(U)=N(GA)
(3)
Moreover,GA+Eis nonsingular and
(4)
In the following lemma, we will proveV(UV)-2UG=0.
Lemma3LetA,T,SandGbe the same as those in Lemma 1. LetVandU*be the matrices whose columns form the bases ofN(GA) andN((GA)*), respectively. Then,
V(UV)-2UG=0
(5)
ProofSince the columns of matrixU*is the basis ofN((GA)*), we have (GA)*U*=0, which is also equivalent toUGA=0. This impliesR(GA)⊂N(U). From Lemma 1, we know thatr(G)=r(GA)=s, which means thatR(GA)=R(G). Then, we haveUG=0and Eq.(5) is followed.

1 Main Results
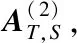
Theorem1LetA,T,SandGbe the same as those in Lemma 1. LetVandU*be matrices whose columns form the bases ofN(GA) andN((GA)*), respectively. DefineE=VU. Then,
(6)
ProofSinceV(UV)-2UG=0, we obtain Eq.(6) immediately from Eq.(4).

Theorem2LetA,T,SandGbe the same as those in Lemma 1. LetPandQ*be matrices whose columns form the bases ofN(AG) andN((AG)*), respectively. DefineF=PQ. Then,
(7)
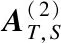
Theorem3LetA,T,SandGbe the same as those in Lemma 1. Then there are two nonsingular elementary matricesUandVof ordern, respectively, such that
(8)
(9)
where matrixB∈Cs×nandscolumns ofBare the same as those ofIs; furthermore,
ProofAccording to Lemma 1, we haver(GA)=r(G)=s, then there are two elementary matricesUandVsatisfying (8) and (9). This means
(10)
Comparing both sides of (10), we drive
(11)
We notice that matricesU2andV2are row full rank and column full rank matrices, respectively, and then, the above four equalities imply that
GAV2=0,U2GA=0
(12)
This implies that
(13)
According to the fact thatr(U)=r(V2)=n-s=dimN((GA)*)=dimN(GA), we obtain

Theorem4LetA,T,SandGbe the same as those in Lemma 1. Then, there exist two nonsingular elementary matricesPandQof orderm, respectively, such that
(14)
(15)
where matrixC∈Cs×mandscolumns ofCare those ofIs; furthermore,
The proof of Theorem 4 is similar to that of Theorem 3.

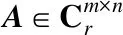
Algorithm1

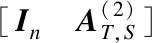
In the following theorem, the computational complexity of Algorithm 1 is analyzed, which only focuses on multiplications and divisions.

(16)

According to the fact thatscolumns ofBare the same as those ofIs, we can directly readV1andV2. In the third step,n2(n-s) multiplications are required to computeV2U2.

n(n+m-1)+n(n+m-2)+…+n(n+m-n)=
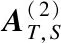
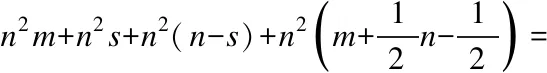
Ifm≤n, the similar algorithm and computation complexities are given as follows.
Algorithm2


(17)
3 Numerical Examples
The Gauss-Jordan elimination is a popular method for computing the inverse of a nonsingular matrix of low order by hand. In this section, Algorithm 1 and Algorithm 2 can be used to compute some famous generalized inverses by hand if the size of matrixAis small by choosing the appropriate parameter matrixG.
Example1[18]Use Algorithm 1 to compute the Drazin inverseAdof matrixA,where

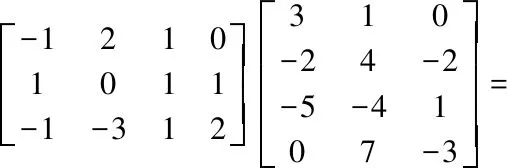
SolutionSimple computation leads to
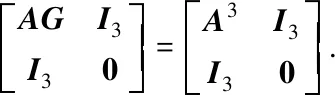


Thus, we haves=1 and
FromU2andV2, in view of Algorithm 1, we have
Finally, perform elementary row operations on [AG+V2U2G]→[I3Ad]

Therefore, we obtain
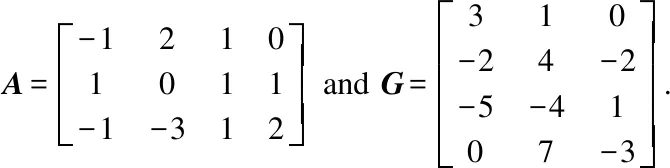
SolutionBy computing, we have

Executing elementary row operations on the first 3 rows and column operations on the first 3 columns of the following partitioned matrix:


This implies
By direct calculation, we can obtain
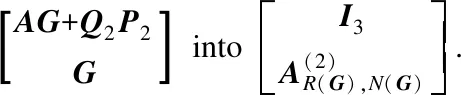

This yields
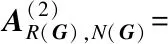
4 Conclusion

杂志排行
Journal of Southeast University(English Edition)的其它文章
- The walking distance decay law of amenity selection based on binary logistic model
- Evaluation of rutting and low-temperature cracking resistancesof warm-mix recycled asphalt bindersunder the secondary aging condition
- Effects of curing age on compressive and tensile stress-strain behaviors of ecological high ductility cementitious composites
- Dispersion of graphene in silane coupling agent aqueous solutions
- The cause of human fatigue and scenario analysisin the process of marine transportation
- Revenue optimization strategy of V2G based on evolutionary game
