既有钢筋混凝土桥梁纵向配筋面积估算公式研究
2020-05-09林启辉王龙辉梁健衡
林启辉 ,王龙辉 ,2,梁健衡 ,2,李 星 ,2
(1、广东建科建筑工程技术开发有限公司广州510500;2、广东省建筑科学研究院集团股份有限公司广州510500)
0 引言
在对既有桥梁进行维修加固时,时常遇到设计资料缺失的情况,无法为加固设计提供配筋信息。已有研究[1-5]根据现场荷载试验,考虑到桥梁构件缺损状况、材质强度、自振频率的影响,同时结合桥梁荷载试验检算系数、承载能力恶化系数、截面折减系数等判定结构或构件的承载能力状况,但没有对加固方法进一步地阐述。虽然《公路旧桥承载能力鉴定方法》[6]附录2中提供了一种估算受拉钢筋面积的方法,但是该方法所计算出的结果与实际情况的差距非常大[7],缺少实用性。因此,本文以正截面抗弯承载能力公式为基础,推导未知配筋梁纵向配筋面积的公式,根据桥梁静载检测数据推算出原有受力钢筋面积,并进行多组试验梁试验以及实际工程数据验证了公式的可靠性,从而为桥梁的维修加固设计提供基础数据信息。
1 理论公式推导
1.1 现有的旧桥钢筋推导方法
依据文献[6]中附录2关于梁桥截面抗弯特性估算方法,如式⑴所示。

式中:Sh为受压混凝土面积对中性轴的面积矩;a为受压截面受拉钢筋面积重心距梁(或板)受拉边缘距离;x为截面中性轴距截面受压边缘的距离。
求得Aa后可按规范有关公式进行截面抗弯特性计算。
上述方法进行钢筋估算只与截面形状有关,与原桥承载能力、桥型、主梁形式等重要因素都无关,所以该公式存在着极大的局限性。
1.2 本研究新方法
本方法以桥梁的静载试验检测结果为依据,以正截面抗弯承载能力公式为基础[8,9],推导钢筋混凝土桥梁的纵向配筋面积公式。
推导公式基本假定:①平截面假定;②不考虑受拉区混凝土拉应力;③不考虑受压区纵向钢筋面积。
在某弯矩M作用下,钢筋混凝土梁的受力图如图1所示。
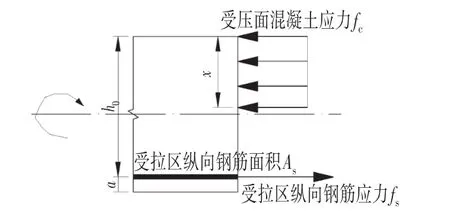
图1 钢筋混凝土梁受力图Fig.1 Tensile Force Diagram of Reinforced Concrete Beam

式中:M为荷载试验中,满足荷载效率时所取用的弯矩值;x1、x2为荷载试验检测时,理论计算、实际状况计算的受压区高度;fs理、fs检为理论、实际检测状况受拉区钢筋应力;fc理、fc检为理论、实际检测状况受压区混凝土抗压强度设计值;As理、As检为理论、实际检测状况纵向钢筋面积;Es为钢筋的弹性模量;h0为截面有效高度;a为梁底到受拉钢筋形心的距离;b为截面宽度;εs理、εs检、εs等效分别为理论计算、实际检测状况、检测状况下理论计算的受拉区钢筋应变;η为静力荷载试验系数;考虑到检测试验荷载试验系数的影响,εs等效=εs检/η。
1.3 公式实际应用
根据静载试验评定桥梁的荷载等级,按理论公式计算桥梁满足该荷载等级的配筋量As理以及此时理论状况下主梁受拉钢筋应变εs理。根据静载试验报告中对应荷载等级下的主梁受拉钢筋应变εs检(在实际工程中,静载试验报告往往给出的是梁底应变,可直接将梁底应变作为梁底纵向钢筋应变εs理,是偏于保守的),再由式⑻即可得出钢筋混凝土主梁的纵向配筋面积。
2 试验梁验证
为验证本文推导出的钢筋混凝土桥梁纵向配筋面积公式的正确性,设计了试验梁荷载试验,试验方案及试验结果如下。
2.1 试验梁设计
为探究不同情况下本文推导公式的准确性,设计了不同截面形式、配筋率、重心位置、混凝土强度等的试验梁。试验梁所用的材料等级[10]如下:混凝土为C30/C50,普通钢筋为HRB335,箍筋为HPB300。
试验混凝土梁分为矩形截面梁与T形截面梁,矩形截面梁的截面尺寸为200 mm(宽)×300 mm(高);T形截面梁的截面尺寸为200 mm(宽)×500 mm(高)×500 mm(翼缘宽)×100 mm(翼缘高)。梁长为2 000 mm,两侧各留100 mm作为支座锚固用,有效长度为1 800 mm。试验所用混凝土梁分为4组,各组梁设计参数如表1所示,试验梁截面配筋如图2、图3所示。

表1 2种截面试验梁设计参数Tab.1 Design Parameters of Two Kinds of Section Test Beams

图2 试验梁矩形截面尺寸及配筋Fig.2 Rectangular Section Size and Reinforcement of Test Beam
2.2 试验方案
试验梁采用简支梁,加载采用三分点两点对称加载,试验采用分级加载,对矩形截面梁按照每20 kN为一级的加载顺序进行加载,对T形梁按照每40 kN为一级的加载顺序进行加载,直至试验梁达到承载能力极限破坏停止加载,试验加载过程中采用钢筋应变计记录跨中位置处钢筋应变,加载装置如图4所示。
2.3 试验结果
试件加载完毕后,变形结果如图5所示。

图3 试验梁T形截面尺寸及配筋Fig.3 T-shaped Section Size and Reinforcement of Test Beam
根据试验数据,当荷载试验系数大于1.15,或小于0.7时,应用本文推导公式计算得出的钢筋面积与实际值误差较大,考虑到当荷载超过试验梁极限承载能力15%后,即荷载试验系数η>1.15,试验梁接近或已处于破坏阶段;当荷载试验系数η<0.7时,受拉区钢筋可能没有到达屈服强度,钢筋有可能还在线弹性变形阶段,钢筋强度没有达到抗拉强度设计值,试验梁此时安全储备较大,这2种情况对实际工程参考意义不大,且根据《城市桥梁检测与评定技术规范:CJJ/T 233-2015》[11]荷载试验系数η范围要求为(0.85,1.05),也限于篇幅,本文只摘取荷载试验系数η范围为(0.7,1.15)的试验数据,试验数据分析见下文(在试验过程中式⑻中的As理取为试验梁的实际配筋值As实配)。
选取符合要求的矩形截面、T形截面梁试验数据如表2、表3所示,矩形截面梁、T形截面梁荷载试验系数与误差关系如图6所示。

图4 加载装置示意图Fig.4 Schematic Diagram of Loading Device


图5 梁开裂破坏状况Fig.5 Cracking and Failure of Beam
对图6分析可知:
⑴ 荷载试验系数η不超过0.97时,当η增加时,误差从负值接近0,逐渐减少;当荷载试验系数η超过1.06后,与真实梁底纵向配筋误差超5%,并且误差此后呈线性增加;

表2 矩形截面梁局部试验数据Tab.2 Local Test Data Sheet for Rectangular Section Beam
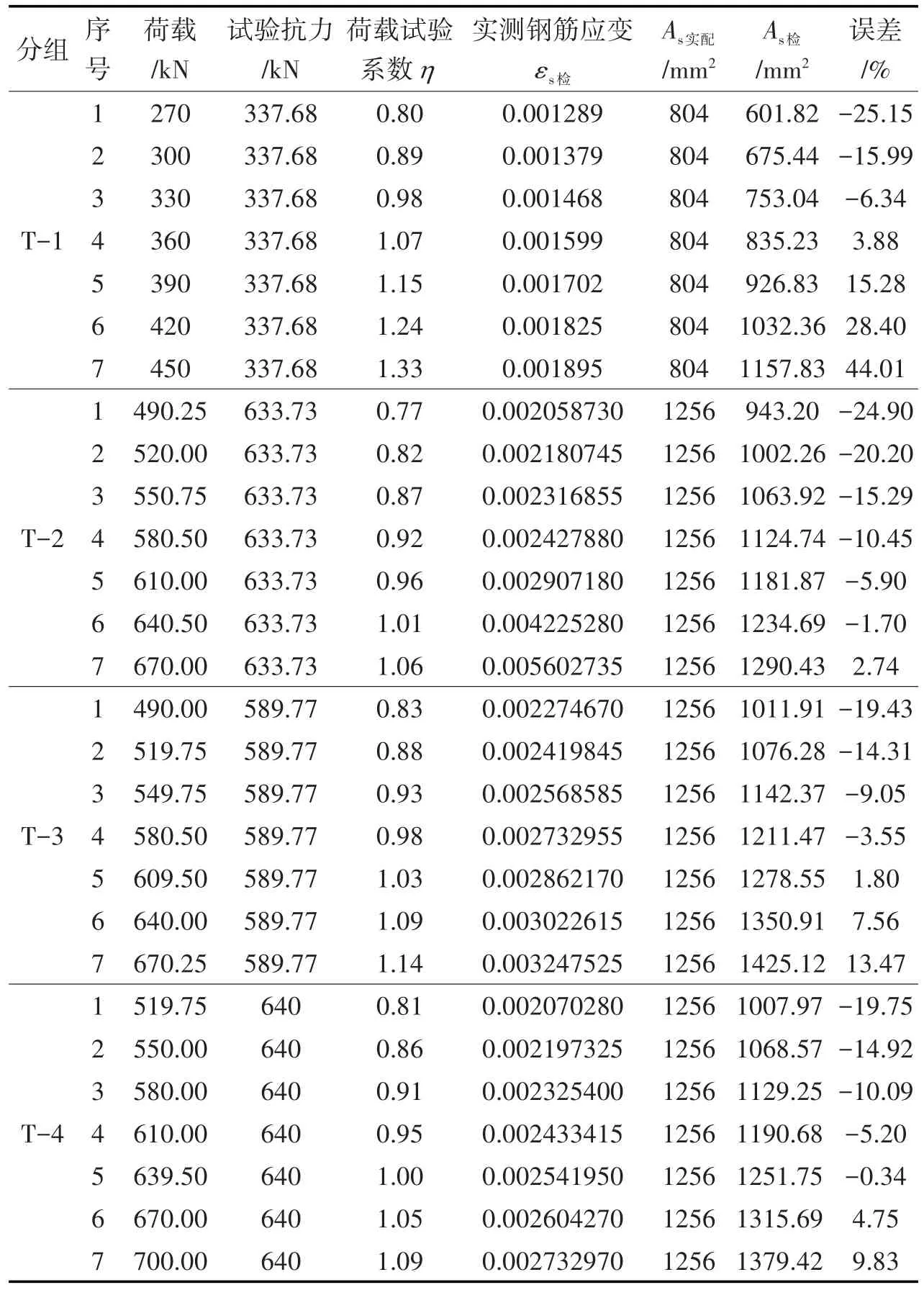
表3 T形截面梁局部试验数据Tab.3 T-shaped Beam Local Test Data
⑵ 不同截面形式、配筋率、重心位置、混凝土强度的矩形截面和T形截面,在荷载试验系数η范围为(0.97,1.07)时,用本文推导出来的纵向钢筋面积计算方法得出的As试与实配钢筋面积As实配误差仅为(-5%,5%),说明本文提出的纵向钢筋面积能很好地适用于不同截面。
⑶ 矩形截面梁与T形截面梁的试验结果相似,当荷载试验系数越接近1,误差越小。当荷载试验系数η在(1,1.04)区间内时,公式推导值与真实值无限接近。


图6 荷载试验系数与误差关系Fig.6 Relationship between Load Test Coefficient and Error
⑷ 对比分析图6a与图6b,可以看出,R-4与T-4的零点在η为(1,1.02)范围内,其他组的零点在η为(1.02,1.04)范围内,这表明当混凝土的强度提高,按本文纵向钢筋面积推导公式计算的结果越接近实际配筋值。
3 实际工程应用
某公路桥梁,跨越河涌,建成于1995年5月,原始设计图纸缺失。该桥全长20.0 m,上部结构为简支T型梁。
该桥的静动载试验结果显示:主梁竖向承载能力不满足公路-Ⅱ级荷载等级的使用要求,需进行维修加固后才能满足公路-Ⅱ级荷载等级的使用要求。
该桥跨径符合标准跨径长度,但是其截面信息(见图7)与同样标准跨径的桥梁不相符,也未能查到与该桥相似的同类型桥梁。

图7 加固梁截面尺寸Fig.7 Section Size of Beam Need to be Reinforced(cm)
⑴ 按照文献[6]钢筋混凝土T型截面梁进行推算:
a=6 cm;x=0.16×(h-a)=0.16×(133-6)=20.32 cm
Aa=Sh/(h-a-x)=83 161/(133-6-20.32)=77 954 mm2
该估算值远远超过了加固桥可能的实际配筋,因此采用文献[6]的计算方法无法准确得到加固桥主梁纵向钢筋实际配筋面积。
⑵ 根据本文推导公式计算该桥的推算纵向配筋:
根据静载检测报告,该桥的试验荷载弯矩:384kN·m,理论计算弯矩值:416 kN·m,荷载试验系数η=0.92,梁底面实测应变值:εs检=188με,理论应变值:εs理=147με。根据式⑻计算得到钢筋面积为7 527.3 mm2。
2012年年底,在对该桥进行加固施工时,凿除主梁混凝土保护层后检查该桥的实际纵向配筋为8根32的钢筋和4根18的钢筋,实际配筋面积为7 451.6 mm2。实际配筋与式⑻计算得到的钢筋面积非常吻合。本文方法推导的钢筋面积、实际配筋面积及文献[6]计算的钢筋面积及对比如表4所示。

表4 加固梁纵筋面积估算比较Tab.4 Comparison of Rreinforcement Area of Beam Need to be Reinforced
4 结论
⑴ 本文以正截面抗弯承载能力公式为基础,推导出了利用静载试验数据计算未知配筋梁纵向钢筋面积的公式。
⑵ 试验梁荷载试验分析了不同截面、不同混凝土强度、配筋等情况下对公式准确性的影响。试验结果表明荷载试验系数越接近1,误差越小,公式越准确。
⑶ 通过实际工程运用验证了本文公式的正确性。本文推导的公式具有较好的准确性和可靠性,值得大力推广,为旧桥加固设计提供原有梁底配筋的计算方法,使得针对缺少原始配筋资料的加固设计有据可依,避免盲目保守设计,从而带来可观的实际经济效益。
