基于Quickprop算法的BP神经网络在边坡稳定性预测中的应用

陈 源，潘宇雄，胡会根，袁厚海

（海南有色工程勘察设计院 海口570206）

0 引言

边坡稳定性分析评价是岩土工程中较为复杂的一项综合性工作，目前多采用野外实际测量数据进行分析研究。然而，受野外测量环境以及测量仪器的影响，分析结果多为不可确定性。除此之外，各种不确定性因素如天气、降水量，以及边坡边界、施工设计参数等的不明确，进一步加大了边坡稳定性的评估难度。经过前人研究，边坡稳定性与上述参数之间很难用理论公式进行模拟表示［1］，要求边坡稳定性分析方法能够较好识别并确定影响因素和稳定性状态之间的联系［2］，因此提出了各种基于已有边坡工程实际检测数据基础上的理论模型［3］。随着人工智能技术的进一步发展，各类智能学习方法已经在岩土工程中得以应用，例如遗传算法［4］，人工神经网络算法［5］，支持向量机预测算法［6］，粒子群优化算法［7］等引入岩土工程分析研究中。

人工神经网络具有较强的建模功能和学习能力，通过对样本数据的学习训练，可以较好地拟合样本数据中输入参数和输出结果之间复杂的数学关系，从而实现对未知结果的预测，对于岩土工程中复杂问题，能够较好地适应参数变量和目标结果之间的数学对应关系，目前得到较好的推广应用。然而，岩土工程由于其受力机制复杂，目标函数的非线性程度高，常规预测方法很难获取受力效应的数学解，且常规的人工神经网络方法存在一些不足［8］，在面对岩土工程的复杂工程特性时，预测效果往往不够理想。黄永恒等人［9］应用BP神经网络实现对岩土工程安全监测数据的预测，并通过优化各类组合后实现岩土工程的预测，取得一定成效。舒苏荀等人［10］采用神经网络改进模糊点估计法进行边坡稳定性分析，取得较好的预测结果。胡军等人［11］提出联合BP神经网络和协调粒子群算法建立CPSO-BP模型，对于边坡稳定性预测精度较高。

岩土工程中，很难判定边坡稳定性有效影响因素以及获取所有相关因素，且上述方法都是通过优化组合方法或者改进输入参数方式等进行预测，没有结合岩土工程的特殊性以及BP神经网络的算法原理对预测的方法原理进行入手研究。因此，本文结合岩土工程自身复杂性质，改进了BP神经网络的构建，采用基于Quickprop算法对预测误差进行归类判断，通过对误差不同方向的导数变化量来对学习速度和效率进行调节，提高神经网络的预测精度。

1 BP神经网络预测方法

1.1 BP神经网络预测原理

人工神经网络（Artificial Neural Network）是近年来迅速发展起来的一种人工智能研究学科，具有较高的数据拟合能力和自适应非线性系统建模水平，在各类学科的应用中拥有巨大潜力。BP（Back Propagation）网络作为一种执行误差逆传播并进行训练的多层前馈网络，具有较好的应用效果，应用也最为广泛［12］。整个网络结构由输入层、隐含层以及输出层组成，每一层由若干个结点（神经元）组成，层间结点通过权值联接，同一层结点之间没有系［13］。经典的三层BP网络结构如图1所示。

图1 经典BP神经网络结构Fig.1 Classical BP Neural Network Structure

网络的训练主要包括信息正向传播和误差反向传播2个阶段，如果误差超过预定的最小误差，则对各层节点之间的连接权值进行调整，从而实现输出误差最小的目的。

BP神经网络采用梯度下降法作为网络的学习算法，定义图1中的输入层、隐层和输出层的各自节点数分别是n，l，m，输入的学习样本为：X1，X2，…，XP，XP=样本中对应的目标输出为：T1，T2，…，网络预测输出为：Y1，Y2，…，YP，

将第p个学习样本输入图1所示的网络结构，则隐层、输出层各自的输出结果分别为：

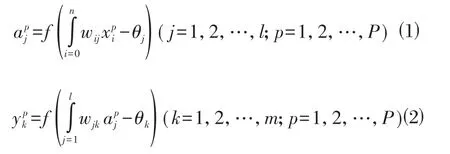
当第p（p=1，2，L，P）个学习样本输入网络后，其均方误差应为输出单元的误差平方和，即：

则所用样本的总误差为：

输出误差极小化通常采用批处理方式或增量方式，输出层实现更新的同时，隐层连接权值和阀值也一并实现更新，则输出层更新调整公式为：

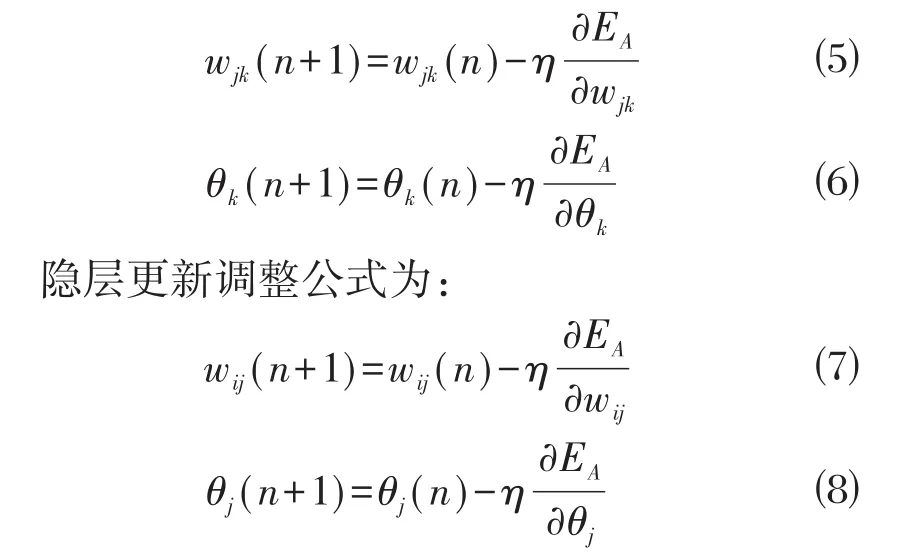
式中：n表示迭代次数；η表示学习速度。

1.2 BP神经网络的改进

标准BP神经网络预测算法的激励函数采用是Sigmoidal函数，该函数的值域为0～1，其一阶导数的区间为0～0.25，导数值最大位置在0点处。网络训练过程中，梯度变化值在接近极小点位置处逐渐趋于0。在训练过程中，为保证网络的收敛性，学习步长取较小的固定值，上述情况的存在，将致使网络收敛速度慢；另外，岩土工程问题通常属于多维建模问题，其求解空间更是一种复杂的多维曲面，且函数空间中存在多个局部极小值点，常规BP神经网络采用最速下降法，其本身只能发现局部极小值点［14］，这便限制了算法的搜索能力，以至于BP神经网络易于陷于局部极小值点。

针对上述存在的问题，本文采用Fahlman提出的Quickprop算法改进BP神经网络学习算法［15］，该算法集中许多最优反传算法的优点，利用误差函数构成的数据平面的弯曲部分信息来加快学习速度［16］。该算法基于误差函数对所有权值的变换函数都是二次曲线，且存在所有权值在同一时刻同时发生变化，而权值的变化不影响误差函数的斜率。因此，根据前一时刻以及当前时刻的权值和斜率，计算曲面抛物线的极小值，则有效计算当前时刻的最优调节量［17］，其表达式为：

式中：△wij表示神经元i和神经元j的连接权值调节量，S（t+1）和S（t）表示误差函数对连接权值当前时刻和前一时刻的偏导数。即：

然而，直接应用Quickprop算法在式⑼会产生很大的调节量，从而使反向调节到极大值点，收敛过程也可能会出现不稳定现象等［18］，因此运用Quickprop算法对BP算法进行改进时综合考虑了梯度下降法，权值改变量的表达式为：

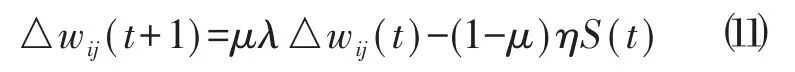
式中：η表示学习速度；μ表示比例系数，为加快网络收敛，比例系数通常取值0.6～0.9之间；λ为调整公式，表达式为：

式中：δ为Fahlman最大增长系数，通常取值为1.75。

改进的算法以常规BP网络构建方式为基础，以图2为例，图2a表示常规BP神经网络结构，其隐含神经元数目为2n-1/（n+1）个，n表示输入层的神经元数目，输出层的神经元数目为1个［18］。通过遍历循环训练之后，网络的全局均方误差趋于稳定，则整个网络停止训练并固定当前隐层输入端的权值。在训练候选隐含神经元时，找到相对最优的隐含神经元是网络学习的目的之一，通常采用逐步寻优法进行计算，并将计算结果引入网络结构（见图2b、图2c）。本文采用改进算法对网络进行调整，通过候选隐含神经元的训练实现输入端权值的调整，在保持原有隐含神经元的输入参数不变的基础上，使得输出端参数可变。当网络的全局均方误差趋于既定误差时，网络训练不在持续，改为进行候选隐含神经元的训练。在新网络的整个迭代训练过程中，网络的输出层和候选隐层神经元交替进行训练，直至整个网络的全局均方误差符合既定目标误差范围。

图2 神经网络Fig.2 Neural Networks

1.3 仿真实验

为验证2种方法对神经网络的收敛性能，采用1个1×10×1的三层网络构成一个零相位波形生成器，输入弧度值，采用2种方法建立的网络进行模拟对比，将弧度值分为120等份，作为训练样本。训练函数为：

将训练样本分别经常规BP神经网络函数和改进后的BP神经网络方法进行测试，对比分析2种网络的收敛性能，2种网络结果如图3所示。

由图3可知，常规BP算法的输出结果在函数的极大值出现“锯齿”跳跃，如图3中黑色虚线所示。改进后的算法，其输出结果中“锯齿”现象消失，跟实际值蓝色曲线吻合得很好，具体如图3中红线所示，二者的测试误差如表1所示。

图3 常规BP网络和改进BP神经网络模拟效果Fig.3 Simulation Effect of Conventional BP Network and Improved BP Neural Network

表1 试验数据处理Tab.1 Test Data Processing

图4是改进算法与常规BP神经网络算法的收敛速度对比图，在进行模拟中，常规BP神经网络的学习速度η为0.15，迭代5 000次后样本的均方误差为0.000 821，网络在整个收敛过程中，误差下降得较平缓。改进算法中，其学习速度η为0.15，最大增长系数δ为1.65，比例系数μ为0.73，网络迭代500次时误差已经下降到0.000 965，迭代1 543次时误差下降到0.000 098 7，此时已认为网络完全收敛。从图4以及表1可看出，改进算法后的BP神经网络显然效果更佳。

图4 常规BP网络和改进BP网络收敛效果图Fig.4 Convergence Effect Diagram of Conventional BP Network and Improved BP Network

2 边坡稳定性分析

2.1 因素选择

影响边坡稳定性的因素较多，经过国内外学者研究，主要因素有边坡角φ、岩土层内摩擦角φ、重度γ、孔隙压力比ru、黏聚力c和边坡高度H［11］，边坡的稳定性是以上因素共同作用的结果。对研究工区的土性进行调查统计，编制土性参数统计表，为后续神经网络模拟参数输入做好铺垫。采用某地区的35个边坡工程实例数据进行测试［19］。为进一步测试本文算法，本文样本数据如表2所示。

图5为2种网络的均方误差和隐含神经元数目关系示意图，可以看出改进BP神经网络算法新增17个隐含神经元，误差收敛到最小，而常规BP神经网络算法要增加28个隐含神经元，增加了计算量，收敛速度更加缓慢。表3是神经网络经过30轮训练的算法性能对比，从表3中可看出改进的BP算法不仅提高了收敛速度，而且改良了训练效果，数据分类的正确率有了明显的提高。

图5 均方误差随新隐含神经元数的误差变化Fig.5 The Variation of Mean Square Error with The Number of New Hidden Neurons

2.2 建立神经网络预测模型

为进一步验证本文改进网络预测边坡稳定性的可行性，再次采用某地区的一组数据进行测试。然后应用本文构建的三层BP神经网络对训练样本进行训练，其参数设置如下，采用Sigmoidal函数作为激励函数，初始权值取0.3，在进行候选隐含神经元训练时，10个候选节点也同步进行训练。

输入样本数据时，需要进行预处理，从而使得网络的训练更加稳定，当输入的样本数据远远大于0时（饱和区段），将导致网络学习速度极度缓慢，严重影响网络的预测结果，因此需要对样本输入进行预处理，预处理公式如下：

经过1 500次的迭代之后，将输出结果和训练样本的误差进行统计，结果如图6所示。

由图6可知，本文改进的BP神经网络预测效果较好，相对常规BP网络而言，网络预测误差较为稳定且维持在一个较小的数值范围内。相对误差最大值为15%，平均误差为3.246%。常规BP神经网络的相对误差最大为52%，平均误差为16.2%，从而有效证实改进后的BP神经网络模型具有较好的预测精度，在工程应用中具有较好的推广性。

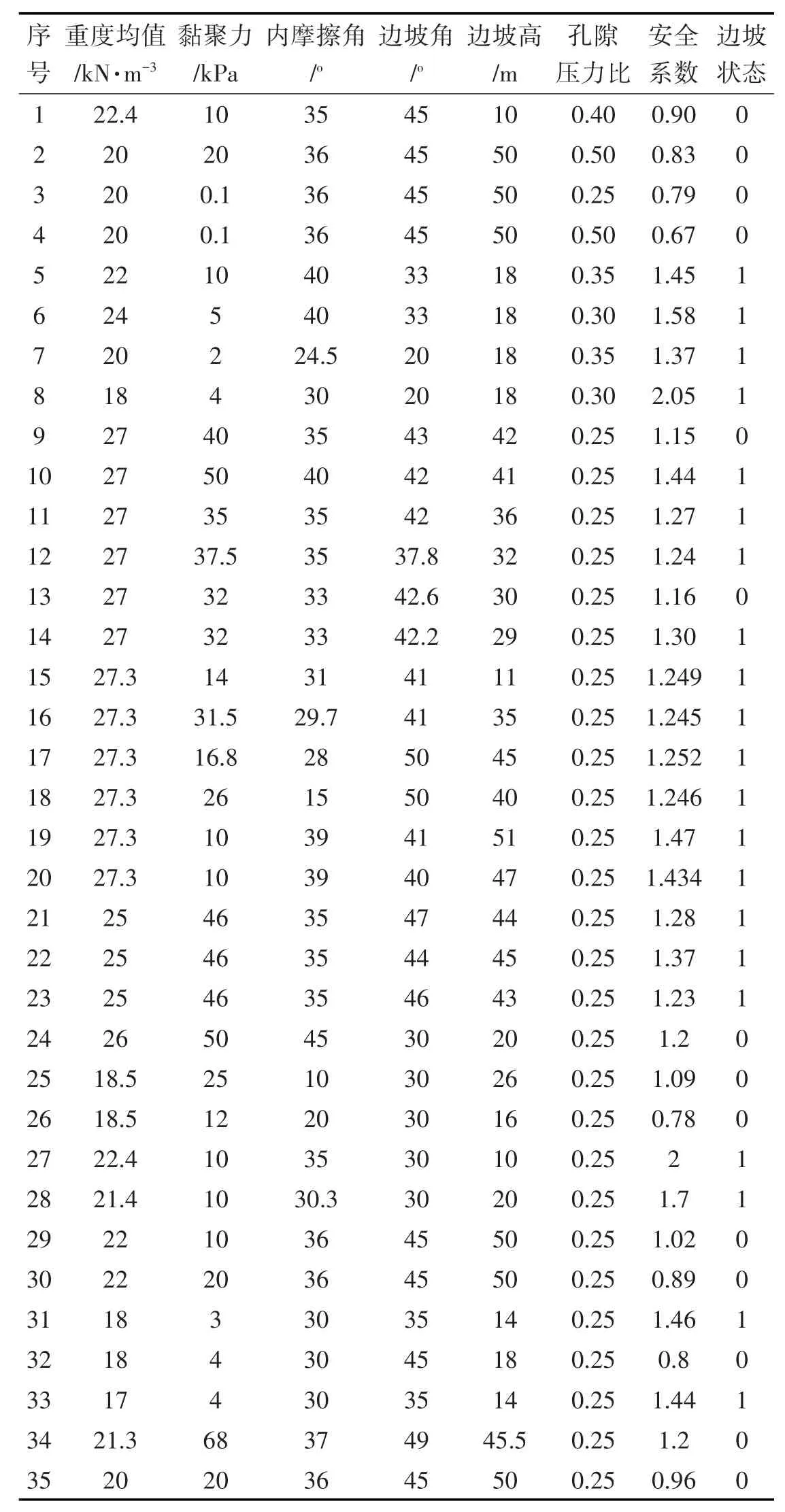
表2 训练样本和检验样本Tab.2 Training Samples and Test Samples

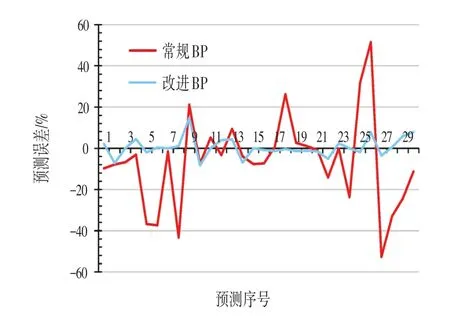
图6 2种网络预测模型于检验样本的相对误差分布Fig.6 Relative Error Distribution of Two Network Prediction Models in Test Samples

为进一步测试本文算法的预测精度，采用棋盘问题来验证改进神经网络问题对边坡稳定性分类能力，采用2007～2017年共10个年度的数据进行测试，将上述的6个参数分为2组，其中重度值，黏聚力、内摩擦角为一组，边坡角、边坡高、孔隙压力比为一组。网络的输出层仅有一个值，即输出为0或1，目的在于检测输入参数所确定的点是否落在棋盘的黑色或者红色方格内。图7a为样本数据的预测结果，图7b为测试数据的网络输出结果，其中样本为600组数据，测试数据为1 300组数据。网络输出值为1表示边坡稳定性安全落在黑色方格内（“·”号表示），网络输出为0时表示边坡稳定性危险落在红色方格内（“+”号表示）。

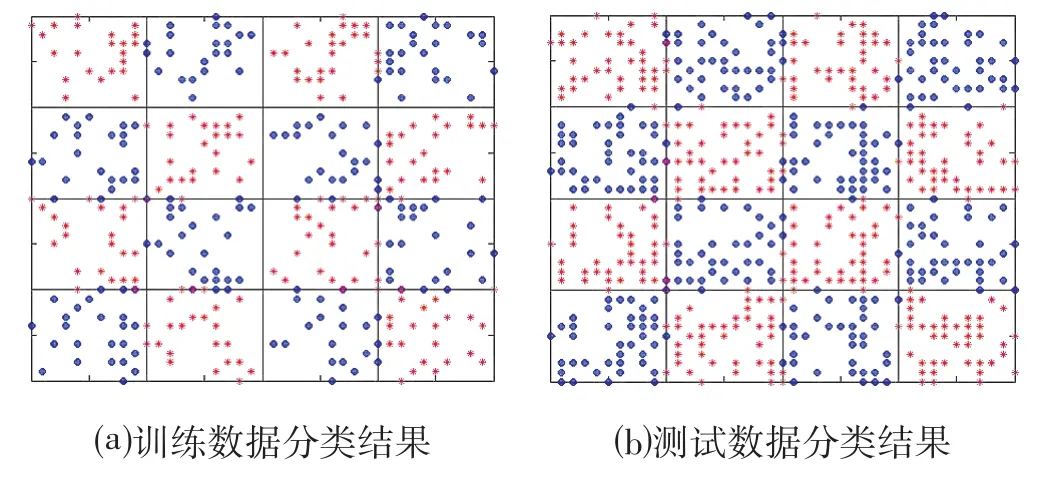
图7 改进神经网络的分类能力棋盘示意图Fig.7 Chessboard Diagram of Improved Neural Network Classification Ability

从图7可以发现，改进的新BP神经万络具有较好边坡稳定性识别分类能力。

2.3 预测结果分析

由图5～图7及表3可见，本文改进的BP神经网络可以取得较好的边坡稳定状态预测结果，与常规BP神经网络预测结果相比，预测精度高，预测效率快。对于通过一个学习样本，改进型的预测误差最大为10%，平均预测误差为3.24%，而常规BP神经网络最大预测误差为53%，平均预测误差为16.2%。

表3 算法性能对比Tab.3 Algorithm Performance Comparison

从本文提出的改进型BP网络的预测结果来看，改进算法具有自适应扩展网络大小以对样本进行学习，对于网络的收敛速度和预测精度均能实现有效提升。

当然神经网络预测也存在一定的局限性，对于学习样本中影响因素种类较少甚至错误数据，其预测结果存在一定的误差，因此如何对已有样本数据中剔除不可靠数据也是该方法需要进一步研究的重点之一。

3 结论

⑴ 岩土工程由于自身相关因素，致使其功能函数难于用显式表达式进行描述，常规的预测方法很难获取较为真实可靠的预测结果。针对上述情况，本文对常规BP网络构建方式以及学习能力进行改进，同时对误差归类和前进方式进行了改善，从而使得改进的BP神经网络在学习方式和预测精度等方面有了明显提高，是其在岩土边坡稳定性预测方面具有较好的应用价值。

⑵ 改进算法通过建立岩土边坡稳定性模型，通过输入黏聚力、内摩擦角以及重度等6个输入参数对稳定性模型进行预测，相关结果显示，新算法提高收敛速度和泛化能力，在预测精度以及预测效率上都具有较好的应用效果，表明改进后的算法所建立的模型预测边坡稳定性是可行的。