基于统一理论框架的故障诊断模型及学习进化方法*
2020-05-09张士刚骆彦廷杨拥民
张士刚,罗 旭,骆彦廷,杨拥民
(国防科技大学 智能科学学院 装备综合保障技术重点实验室, 湖南 长沙 410073)
当前在工程中使用的故障诊断方法有基于数据驱动的方式、基于模型的方式、数据和模型结合的方式等不同种类。基于数据驱动的方式需要大量的实验或实测数据进行模型训练,这在新研制装备或者无良好数据记录的装备上是不适用的。基于模型的方式对模型的精度有较高要求,其适用于工作原理清晰的装备,缺点在于精确模型建立复杂。数据和模型结合的方式是当前研究的热点之一。达到这一目的的关键在于采用一种合理的模型,既能实现对先验知识的表达又能较好地将数据融入模型中。
概率图模型是大的知识表达模型。贝叶斯网作为其中的模型之一,由于具有明确的物理意义,在故障诊断领域已得到了较好的应用[1-3],并且表现出良好的发展和改进前景。按照概率图理论研究专家美国斯坦福大学Koller教授的说法,概率图是少数同时集表达、推理、学习三种能力于一体的框架模型之一[4]。该模型相关的特性和故障诊断所面临的问题有诸多共通之处,受到了国内外学者的普遍关注。Pattipati教授所带领的团队以概率图理论为基础提出了动态多故障诊断(Dynamic Multiple Fault Diagnosis, DMFD)模型[5-6]、因子隐马尔科夫模型[7](Factorial Hidden Markov Model, FHMM)、耦合因子隐马尔科夫模型[8-9](Coupled FHMM, CFHMM)等多种动态故障诊断模型,有效解决了动态故障诊断、不确定性条件下的多故障诊断等问题;Li等研究了动态贝叶斯网在飞机机翼健康监控数字孪生中的应用[10];Cai等研究了贝叶斯网在瞬时和间歇故障诊断中的应用,对模型的构建和应用方法进行了阐述[11-12];于寄语研究了贝叶斯网在机械故障检测中的应用[13]。除了模型的应用方法,在模型构建方面,当前也有不少学者进行了理论和方法研究工作,比如Campos等研究了基于信息熵简化搜索空间的贝叶斯网构建方法[14];Andrews等研究了混合变量情况下的贝叶斯网评分方法[15];Scutari等对三种不同类型的贝叶斯网模型学习方法进行了对比研究,包括基于约束的方法、基于评分的方法和二者结合的混合算法[16]。
总的来看,国内外学者在概率图理论方法或者概率图在故障诊断的应用方面均有不少研究工作,但大部分的研究是针对应用、学习或者推理的某一方面,而未对模型构建、不同场景下的诊断应用、预测方法、学习进化等方面进行统一的阐述。本文在系统梳理总结已有研究成果的基础上,研究了多模式系统的诊断模型构建方法,形成了基于概率图的故障诊断模型及学习进化统一理论框架。系统阐述了该模型在故障诊断领域的应用场景,包括模型构建、多模式情形下的模型、动态故障诊断模型、诊断模型学习进化方法等内容,并指出了在该理论框架下下一步可进行深入研究的方向。研究过程中涉及的主要模型及其特点如表1所示,其中序号7-11所示的模型为下一步可深入研究的模型。

表1 研究涉及的模型及主要特点Tab.1 Characteristics of the models discussed in this research
1 贝叶斯网与故障诊断
贝叶斯网是一种基于网络结构的有向图解表示,是基于概率分析、图论的一种不确定性知识表达和推理模型,是一种将因果知识和概率知识结合的信息表示框架。具体来讲,贝叶斯网是由节点以及连接节点之间的有向边及其中的概率参数组成的。在故障诊断中,主要考量的是故障模式和测试之间的关系。与之相对应,诊断贝叶斯网所包含的元素也主要由这些变量组成。其中,测试量和故障模式分别映射为变量,它们之间的影响关系映射为有向边。如图1所示,为某发动机诊断贝叶斯网的部分结构,其中包含了喷油器雾化不良、喷油器阻塞两种底层故障模式,这两种故障模式发生时均可导致燃烧不良,所反映出来的征兆包括缸内爆压偏低、功率降低、油耗偏高等可测特征。

图1 诊断贝叶斯网示例Fig.1 Example of diagnostic Bayesian networks
变量节点由不同的状态组成,节点之间通过相关性概率表(条件概率表)表示相关性强度。如表2所示,为节点“燃烧不良”所对应的概率表。依据表中的内容,若喷油器雾化不良未发生、喷油器阻塞发生时,燃烧不良的概率为0.7。其他状态组合时的参数具有类似的含义。
表2“燃烧不良”节点条件概率表
Tab.2 Conditional probability distribution table of the poor combustion node
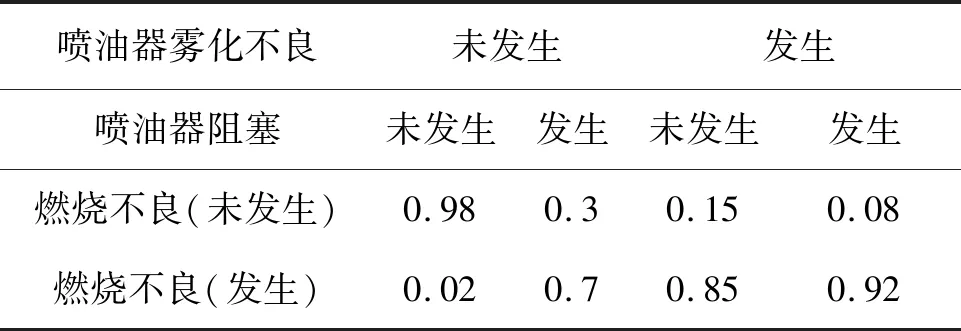
喷油器雾化不良未发生发生喷油器阻塞未发生发生未发生发生燃烧不良(未发生)0.980.30.150.08燃烧不良(发生)0.020.70.850.92
实现基于贝叶斯网诊断的关键在于针对具体装备构建出类似图1所示的贝叶斯网,并且基于实测数据进行推理计算。诊断的过程为给出故障征兆或者测试数据推理得出诊断结论的过程。在实施过程中,首先将测试量或已知征兆按照实测值设为证据变量,然后进行推理计算,可得出其他变量不同状态的发生概率。依据故障变量的概率,可判断是否有故障发生。以图1所示的贝叶斯网为例,假设系统有功率降低和油耗偏高两种征兆,经过推理后,得出的故障发生概率分别为:燃烧不良0.995,喷油器雾化不良0.708,喷油器阻塞0.648。可以判断柴油机系统发生了燃烧不良的问题,故障原因可能是喷油器雾化不良和阻塞,雾化不良的概率高于阻塞。
2 诊断贝叶斯网构建方法
在一般情况下,贝叶斯网的构造方法有两种:一种是通过咨询专家手工构造,另一种是通过数据分析,利用机器学习的方法来获得贝叶斯网。但是经过总结可以发现,无论哪种方法,要么需要大量的实际测试数据,要么需要进行大量的分析设计工作,工作十分复杂。在实际工作中,尤其对于一种新装备来说,往往无法提供大量的故障数据供贝叶斯网的学习使用,严重限制了这种方法的应用。
在现代装备设计过程中,除了功能要求以外,对装备的测试性、维修性、可靠性等通用质量特性普遍提出了要求。测试性建模是其中的关键工作内容之一。为此,可采用基于测试性模型的贝叶斯网自动构建方法来简化贝叶斯网的构建过程[17]。从测试性分析与设计的角度来看,在测试性建模过程中已经对系统的结构、故障模式及测试之间的关系进行了大量分析工作。充分利用这些先期工作,减少重复劳动并提供一种通用的自动构建诊断贝叶斯网的方法是一件十分有意义的事情。具体实现方案如图2所示,其中接口文件和所构建的贝叶斯网为示意图。接口文件主要是相关性矩阵,表示的是故障(f1~f4)和测试(t1~t4)之间的相关性。具体而言,元素1表示对应列的测试可以检测到对应行的故障,元素0表示不可检测。贝叶斯网构建的主要思想是实现测试和故障及其相关性关系到节点及有向边的映射[17]。当前该方案已经在发动机、装甲车辆、航天产品等装备上进行了初步应用。实施过程中,首先采用TEAMS软件构建系统的测试性模型(即多信号流图模型),对系统进行测试性分析,进行传感器优化设计[18];然后,生成以相关性矩阵为主的接口文件;在此基础上,依据因果关系的一致性,构建诊断贝叶斯网模型,用于诊断和推理。

图2 诊断贝叶斯网构建方法示意Fig.2 Example of diagnostic Bayesian networks constructing method
3 动态故障诊断方法
普通的贝叶斯网是一种静态结构,无法有效表达故障的演化信息。而实际上,当前的故障状态和上一时刻的故障状态密切相关,故障也可能会存在传播和时延的问题。针对这一复杂故障情形,需要更为强大的模型。因此,基于贝叶斯网和马尔科夫相关理论,研究提出了一种动态故障诊断推理模型[19],故障演化、耦合关系等动态参数可得到有效表达,如图3所示。

图3 动态故障诊断模型Fig.3 Dynamic fault diagnosis model
在该模型中,不同的故障模式通过单个马尔科夫链进行表征。每一个圆圈表示故障状态,方块表示测试值。模型中的有向边表示故障和故障之间或者故障和测试之间的相关性关系。在实际系统中,不同故障之间的关联关系表示故障耦合,故障和测试之间的关系表示测试关系。这些关系的发生可能存在时间延迟,表示故障传播时间和测试时延。
该模型将故障的动态特性引入诊断推理过程中,可适用于复杂非线性系统的诊断。同时,由于模型可表达故障之间的关联关系,该模型具有一定的耦合故障诊断能力。和常规的故障诊断不同,基于该模型的故障诊断需要考虑测试的时序问题。推理过程中,可选择时间窗迭代计算的方法,即选取一段时间的测试结果,进行推理计算,得到该窗口内的故障状态。随着新的测试结果的加入,逐步移动诊断窗口,更新诊断结论。基于该思想,前期研究中提出了部分采样算法和分块坐标上升-维特比算法[19],可用于工程中的诊断推理。
4 多模式系统故障诊断方法
针对大部分系统而言,其工作状态不可能一成不变,并且不同工况之间还可能存在过渡状态。在不同运行工况下,故障的特征可能不尽相同,测试正常与否的判决方式也不尽相同。这类变工况系统的故障诊断也称为多模式系统故障诊断。针对这一问题可采用下述两种方案进行建模。
4.1 变结构贝叶斯网
普通的贝叶斯网一旦结构确定就不会再发生变化,这不适用于变工况系统的故障诊断。变结构贝叶斯网的提出为解决这一问题提供了一种新的思路。变结构的含义为依据诊断网络中某些变量取值的不同,有些边的相关性会发生改变。其中最典型的是环境独立贝叶斯网[20-21],如图4所示。其中c表示环境控制变量,f3到t4之间边上的参数表示只有当c=1时该相关性关系才会存在。如果c表示某一工况参数,则表示只有在工况代码为1时f3和t4之间才有相关性关系,这和多工况故障诊断过程及需求具有一致的含义。

图4 环境独立贝叶斯网Fig.4 Context-specific independence Bayesian networks
为了更加直观地表达变结构信息和实现贝叶斯网的构建,在此可将工况变化信息抽象为一个节点,通过参数的相关性设置实现变结构的表达。和第2节所示的单模式下的贝叶斯网构建方法不同,在这种变结构情况下,贝叶斯网的构建和参数设置方式如下所述。
1)对系统相关性进行分析和表征:建立系统的多模式测试性模型,对系统进行分析,得到一组共两个相关性矩阵。假设系统共有m个故障模式,n个测试,k个开关。第一个矩阵表达故障和测试之间的相关性关系,即D1=[dij]m×n,其中dij∈{0,1},取值为0表示第j个测试在任意模式下均无法检测到第i个故障;取值为1表示第j个测试可以检测到第i个故障。第二个矩阵表达的是开关和测试的相关性,用D2=[rij]n×k表示,其中rij∈{0,1},取值为0表示第j个测试和故障的相关性不受第i个开关状态的影响;取值为1表示第j个测试和故障的相关性和第i个开关的状态相关。
2)确定多工况系统贝叶斯网的结构:依据贝叶斯网的定义,贝叶斯网的结构包括节点以及节点之间的连接关系两部分。在变结构系统中,贝叶斯网由两层共三类节点组成。第一层为故障和开关层,分别用故障节点和开关节点表示。第二层为测试层,用测试节点表示。故障节点和故障模式相对应,共有m个。开关节点和开关相对应,共有k个。测试节点和测试相对应,共有n个。
在确定好节点数目和类型后,为节点之间添加连接关系。添加的方式依据两个相关性矩阵进行,具体为:针对矩阵D1=[dij]m×n,如果dij=1,则在第i个故障(用fi表示)和第j个测试(用tj表示)之间添加连接关系,方向由fi指向ti;针对矩阵D2=[rij]n×k,如果rij=1,则在第j个测试(用tj表示)和第i个开关(用si表示)之间添加连接关系,方向由si指向tj。
3)确定变结构系统贝叶斯网的参数并采用树形结构进行表征:针对故障节点,设置正常和异常两种状态,异常概率表示故障率。针对开关节点,设置开和关两种状态,概率分别设为0.5。针对某一个测试节点,用集合E={F,S}表示初始备选节点集,其中F表示与其相关的故障节点,S表示与其相关的开关节点。从集合E中选择相关故障节点数目最多且不为0的开关节点作为下一步的树节点。针对开关闭合分枝,从E中去除该开关节点;针对开关断开这一分枝,从E中去除该开关节点以及和该开关相关的故障节点,更新E。若无开关节点,选择故障率最高的故障节点作为下一步的树节点,从E中去除该故障节点,更新E。针对故障存在这一分枝,存储参数1,停止扩展该分枝;针对故障不存在这一分枝,若E中不包含其他故障节点,存储参数0,否则,继续选择节点,扩展参数表达树,直至达到停止条件。最终所得的二叉树即为测试节点的参数。
以某系统为例,假设m=3,n=2,k=2。如图5所示,f1~f3为三个故障节点,t1~t2为两个测试节点,当s2闭合时,f3和t1相关,否则不相关。

图5 变结构系统Fig.5 Multimode system
则可得到两个矩阵分别为:
(1)
(2)
所得到的变结构贝叶斯网如图6所示。节点t1的参数设置如图7所示。

图6 变结构系统贝叶斯网Fig.6 Bayesian networks of the multimode system
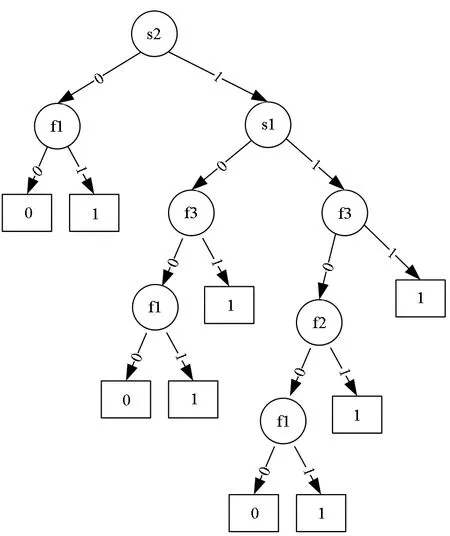
图7 t1节点的参数设置Fig.7 Parameters of node t1
除了t1以外,其他的参数设置方式和传统的贝叶斯网一致,比如,针对故障节点(即f1, f2, f3),每一节点均有两种状态:正常和异常。异常的概率即故障率,假定三个故障率分别为0.1、0.3和0.6。针对开关节点(即s1,s2),每一节点有两种状态:开和关。两者的发生概率均设为0.5。
为了证明方法的有效性,在此采用贝叶斯网建模和推理工具GeNIe进行仿真分析[22]。假定每个故障模式均有两个状态——good和bad,测试有pass和fail两个状态,分别表示测试正常和异常。仿真过程中假设测试t1异常,t2正常,当s1打开、s2闭合时,诊断结果如图8所示。此时,f2没有被任何测试检测,故其故障概率为原始故障率0.3。以此为基础进行推理,f1可确定为异常,f3可被t2完全排除。
当s1和 s2均闭合时,结果如图9所示。此时t1可检测到f1、f2和f3。f3可被t2完全排除,f1、f2的经推理后的故障率分别为0.27和0.81,均比原始概率有所提升,符合实际情况。

图8 s1打开、s2闭合时诊断结果Fig.8 Diagnostic result that s1 is open and s2 is closed

图9 s1、s2均闭合时诊断结果Fig.9 Diagnostic result that both s1 and s2 are closed
4.2 变结构动态故障诊断模型
如果实际系统中的故障情形比较复杂,故障具有动态特性,则多模式系统故障诊断可用变结构动态模型进行建模[23],如图10所示。

图10 变结构动态诊断模型Fig.10 Multimode dynamic fault diagnosis model
该模型主要由两部分组成:第一部分为若干个第3节所述的动态诊断模型,分别代表不同工况下的诊断网络,它们的相关性参数以及故障集合可能不同;第二部分为控制网络,可以认为是一个马尔科夫模型,用来确定系统的工况或模式。实际诊断推理过程中,首先基于部分测试信息进行推理,依据控制网络确定系统当前的状态,对系统工况进行判定。然后依据确定的工况自动选用合适的动态诊断推理模型,进行参数调控,获取推理模型,并进行推理计算,得到系统当前的故障状况。不同工况下的模型可以通过过渡状态进行连接。在过渡状态,模型参数依据控制网络状态变量的取值进行合理设置。
5 故障诊断与预测一体化方法
随着状态监控理念的进步,故障不只是要求能进行诊断,而且要求能尽可能地提前预知,即故障预测。在前文阐述的动态诊断模型中,虽考虑了时间要素,但测试只和等于或比它时刻早的故障相关,即只考虑了时延现象。事实上,故障预测和时延在时间参数上是相反的关系,通过对模型进行改进,测试可以和以后时刻的故障状态相关,则可以实现对故障预测信息的表征,达到利用统一模型实现故障诊断和预测一体化的目的。如图11所示[24],原有的诊断推理算法经过时间变换即可用于故障预测推理[25]。

图11 含故障预测的动态诊断模型Fig.11 Dynamic fault diagnosis model considering fault prediction
基于该模型,针对某航天器电源系统进行了仿真计算,某次计算结果如图12所示[25]。

图12 故障预测案例结果Fig.12 Result of a fault prognosis case
在图12中,横坐标表示时刻点,纵坐标表示故障索引。仿真过程中,首先注入某个故障模式,生成测试数据;然后,利用该测试数据和诊断模型按时刻顺序依次进行诊断推理,比较推理结果和实际注入的故障,如果二者一致表示诊断结果正确,如果可以对未来的故障状态进行提前输出,证明模型具有一定的故障预测能力。在图12中,“*” 表示在验证过程中注入的故障模式,方框表示采用诊断模型的诊断推理结果。图中所展示的是诊断推理到30时刻时(即图中所示竖线表征的时刻)的诊断状态。由图示结果可以看出,诊断模型不仅给出了30时刻以前的状态,而且还给出了未来两个时刻的状态,并且和实际注入的故障一致,表明了诊断模型具有一定的故障预测能力。需要说明的是,达到这一目的前提是所构建的模型具有和实际系统相符的合理结构和参数。
6 诊断策略学习进化方法
贝叶斯网等概率图故障诊断模型的构建依赖于先验知识。然而,当前装备的相关知识是在设计阶段就设计确定的。由于系统设计时运维知识有限,对运行环境的认识不够,或者针对新研制装备本身就缺乏相应的故障知识积累,在诊断策略使用过程中经常存在“水土不服”的现象。尤其是新研制的装备,诊断系统虚警率高、维修策略不符合实际等问题反映强烈,影响了装备的可用性。为此需要研究一种既能利用设计时的先验知识又能随着使用数据积累进行能力增强的机制,为实现智能自适应诊断提供一条新的解决途径。在此可采用一种通过参数学习和结构学习改进诊断策略的方法。其基础模型为前文所讨论的贝叶斯网等诊断模型,参数学习采用最大似然估计的方式,结构学习采用改进的评分-搜索策略,基本思想如图13所示。

图13 利用结构学习方法改进诊断模型的流程Fig.13 Procedure of fault diagnosis model improvement using structure learning
为了验证方法的有效性,采用仿真的方法进行了验证。仿真策略为:首先随机生成诊断模型,然后基于该模型生成一组采样数据。将模型随机删除部分边,然后再采用学习算法进行学习改进,得到学习后的模型。基于原始模型、删除边后的模型、学习后的模型采用相同数据进行模拟诊断推理,进行结果对比并判断学习效果。某系统的仿真结果如表3所示。其中正确检测率指的是故障状态被正确检测出的比例,错误检测率指的是正常状态被错误地隔离成故障的比例。可以看出,和删除边后的模型对比,参数学习后和结构学习后的模型诊断结果均有提升,接近或好于原始模型,从而证明了方法的有效性。更为深入和详细的阐述可参考文献[26]中的研究。

表3 学习结果对比Tab.3 Comparison of the learning result
7 模型的研究改进展望
1)隐变量与未知故障:在贝叶斯网构建过程中,故障模式可能考虑得不够完善,即变量集合不够全面。在使用过程中,可能会存在数据和模型不符的现象。通过贝叶斯网隐藏变量的学习,有可能发现未知故障,提高对系统故障模式的认识水平并为改进诊断策略提供支撑。
2)局部诊断模型优化:复杂结构的贝叶斯网运算量较大,使用过程可能存在推理时间过长的问题。实际工程中,可依据实际状况研究模型局部优化措施,比如因果独立假设等,增强实用性。
3)复杂变量情形下的推理:在诊断系统中,测试量有连续量也有离散量。当前常用的诊断贝叶斯网以离散量为主,如何实现混合变量情形下的建模和诊断推理是需要研究的问题之一。另外,可能还存在部分变量可观测的情形,如何进行学习改进和优化是需要研究的内容。
4)分层及分布式故障诊断:复杂系统往往由很多部件组成,并且具有复杂的层级结构。实际诊断过程中,诊断层级不一定到故障模式,到可更换单元即可满足要求。另外,由于系统单元模块多,采用单个模型复杂度很高,在诊断效率上无法满足应用要求。如何针对复杂系统实现分层诊断和分布式诊断是非常有意义的研究内容之一。
8 结论
1)对基于概率图的诊断推理模型进行了阐述,提出了基于统一理论框架的故障诊断模型这一理念,研究了针对多种应用场景的故障诊断整体技术方案。
2)研究了统一理论框架下的贝叶斯网构建、动态故障诊断、多模式故障诊断、预测和诊断一体化推理、诊断模型学习改进方法等内容,对各模型之间的关系进行了阐述,给出了部分模型的仿真结果,验证了方法的有效性。
3)对模型的进一步发展进行了展望。
