采用优化加点Kriging模型的助推火箭残骸安全区预示方法*

祝学军，卜奎晨，王 浩，高 峰，赵长见

(中国运载火箭技术研究院， 北京 100076)

飞行安全区，又称飞行安全控制区，是指火箭实际飞行时，可能使发射场、航迹区的人员、设施遭受损伤和破坏的区域[1]。根据火箭正常飞行或故障飞行情况，可将安全区划分为发射场安全区(或称为首区安全区)、子级残骸安全区、航区安全区及落区安全区。由于飞行安全区是火箭正常飞行时分离残骸或者异常飞行时的自毁残骸可能到达的区域，该散布区域大小与火箭性能和飞行环境密切相关，因此在进行安全区计算时需要考虑各种偏差和干扰的影响，如发动机性能偏差、结构质量偏差、气动偏差、大气偏差及风干扰等。

传统弹道式飞行器采用抛物线弹道，大部分弹道位于真空中，飞行器在大气层内飞行的时间较短，气动偏差、大气偏差及风干扰等因素对安全区范围影响相对较小，传统弹道式飞行器在进行飞行安全区计算时，往往采用几种主要偏差极限叠加的方法进行安全区计算，计算方法偏保守。由于我国经济不断发展，人员经营和活动范围不断扩大，航天发射可用区域不断缩小，导致发射场安全控制实施难度不断加大。传统极限偏差叠加的安全区计算方法因过于保守已不再适用。

相比传统弹道式飞行器，助推滑翔飞行器的助推火箭残骸在大气层中飞行的时间更长，受大气环境和气动力偏差的影响更严重，其分离残骸安全区范围显著增大，进一步加大了发射场安全控制实施难度，此外，还存在对发射时间选择等方面的需求，对安全区精细化设计需求更高。

国内外学者在飞行安全区精细化计算方面开展了较多的研究工作[2-4]，并取得了一定的成果。文献[1]采用Monte Carlo方法进行了运载火箭残骸落区的计算，有效地减少了安全防范区域。文献[2]针对火箭在不同季节、不同月份发射的飞行包络开展了打靶仿真，用于确定发射时间。但由于偏差组合工况过多、仿真时间不充裕，无法满足使用的需求，为此采取了选取恶劣工况的方法来降低仿真次数。可见，Monte Carlo方法将安全区范围、偏差项及发生概率建立了关系，是一种较为精细化的安全区计算方法，但当计算工况较多时，存在仿真时间过长的问题。国内外学者针对如何确定Monte Carlo方法打靶次数开展研究[5-6]，并得出“对于一般的工程技术问题，打靶次数3000～5000即可满足工程精度要求”的结论。但由于存在需要单独施加偏差(如风干扰)及需对发射时间(不同季节、不同月份)进行选择等问题，打靶次数仍然会大量增加。为了进一步加快仿真速度，近年来在采用代理模型加速Monte Carlo打靶方面也有一定的研究，文献[7-8]分别针对Kriging模型开展了相关研究，并取得了一定的成果。

本文结合Monte Carlo方法和代理模型的特点，提出了一种基于优化加点Kriging模型的助推火箭残骸安全区分析方法，为助推火箭残骸等安全区预示提供理论参考。

1 弹道计算模型

1.1 运动方程

火箭及分离残骸的弹道计算质心运动动力学方程和绕质心转动动力学方程[9]见式(1)和式(2)。

(1)

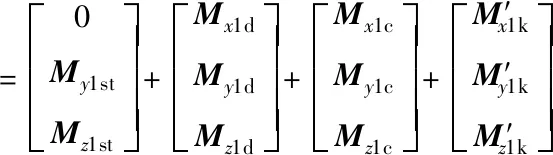
(2)

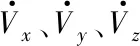
质心运动学方程见式(3)。

(3)

式中，x、y、z为发射系位置分量，Vx、Vy、Vz为发射系速度分量。

为防止姿态角解算出现奇异问题，采用四元数方法进行姿态角解算处理。基于四元数的绕质心转动运动学方程见式(4)和式(5)。

(4)

(5)

式中，q0、q1、q2、q3为四元数，φT、ψT、γT为姿态角。

1.2 主要偏差情况

在针对助推火箭残骸散布区域等进行安全区计算时，需要考虑助推段发动机性能偏差、质量特性偏差、气动系数偏差、大气偏差(温度、密度、压强)、风干扰等不确定干扰因素，同时考虑残骸飞行段的气动系数偏差、大气偏差及风干扰等不确定干扰因素。干扰因素的分布规律依赖于统计数据，一般可以认为发动机性能偏差、质量特性偏差、气动系数偏差、大气偏差等服从高斯分布，记为：

(6)

发动机性能偏差一般包括发动机推力偏斜、发动机工作时间偏差、推力偏差和总冲偏差等。

风干扰一般取为常值项，风速大小VW随飞行高度变化，计算公式见式(7)。由于风向或射向的不确定性，通常按照顺风、逆风、左侧风、右侧风四个工况分别施加并针对其他偏差项进行模拟打靶分析[3]。

VW=f(h)

(7)

2 安全区预示方法

2.1 安全区预示模型

在不确定性干扰因素的影响下，工程上残骸安全区范围通常假设为某一矩形区域，由纵向最远距离εymax、纵向最近距离εymin、横向最远距离εxmax、横向最近距离εxmin构成。结合助推火箭及分离残骸弹道运动方程，综合考虑分离残骸运动过程中的不确定性因素影响，假设分离残骸运动的某一组不确定性干扰因素为Pi=[Pi1,Pi2,…,Pin]T，残骸落点距离发射点的纵向距离为Y(Pi)，横向偏移距离为X(Pi)。则残骸安全区预示模型如式(8)所示：

(8)

式中：Pr(·)表示残骸落入某一区域的概率；P表示所有组不确定性干扰因素；Pfy1,Pfy2,Pfx1,Pfx2为对应的目标失效概率。残骸安全区预示问题的物理意义在于高效寻找安全区域的阈值εymax,εymin,εxmax,εxmin，使得残骸落在该阈值之外的概率等于给定的目标失效概率Pfy1,Pfy2,Pfx1,Pfx2，从而确定残骸安全区域。

针对这一模型，常规的Monte Carlo方法需针对所有不确定干扰因素进行大量的打靶分析，对残骸落点结果进行统计，确定安全区域的阈值，给出满足目标失效概率要求的安全区域范围，这一方法体现了概率设计思想，符合实际物理意义，此外Monte Carlo方法具有非侵入性和无偏性，能够给出精确的安全区预示范围。然而，Monte Carlo方法需要大量调用弹道仿真模型，导致计算效率较低，时间成本较高，难以满足快速设计迭代的工程需求。针对这一问题，本文提出了一种基于优化加点Kriging模型的安全区预示方法，结合Monte Carlo和代理模型的特点，通过序列优化加点策略自适应更新代理模型，直至满足收敛条件，进而结合Monte Carlo方法高效完成概率安全区分析计算。

2.2 Kriging模型

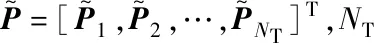
(9)

式中，f(P)=[f1(P),f2(P),…,fn(P)]T为回归基函数，β=[β1,β2,…,βn]T为回归系数，fT(P)β项对真实模型进行全局性近似。z(P)为服从高斯分布N(0,σ2)的随机过程，两个训练样本点Pi和Pj之间的协方差定义为：

Cov[z(Pi),z(Pj)]=σ2R(Pi,Pj),i,j=1,…,NT

(10)

式中，R(Pi,Pj)为相关函数，表征Pi和Pj之间的空间相关性，本文选取服从高斯分布的相关函数[11]。

利用对数似然函数，分别对式(9)的回归系数β及式(10)中的方差σ2求导，给出两者的极大似然估计：

(11)

(12)

(13)

进而，针对某一组不确定性干扰因素Pi，Kriging模型在给出预测值的同时，还可以进一步给出预测值的预估标准差，服从如下高斯分布：

(14)

2.3 优化加点Kriging策略

为了进一步提高安全区域分析计算的求解效率，提出了一种基于优化加点Kriging模型的高效概率安全区预示方法。以求解纵向最远阈值εymax为例，根据识别的分离残骸干扰因素分布类型及其分布参数，在整个随机概率空间选取一定数量的Monte Carlo样本点集PMC，结合纵向最远阈值的目标失效概率Pfy1，为保证样本点集PMC的相关系数不大于0.05，Monte Carlo样本点数量NMC满足如下条件：

(15)

(16)

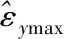
(17)

(18)

综上所述，分类失效概率可以表达为如下形式：

(19)

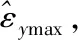
2.4 安全区预示流程

基于优化加点Kriging模型的安全区预示方法流程图如图1所示。

图1 基于优化加点Kriging模型的安全区预示流程图Fig.1 Flow chart of prediction method for safety control zone based on infill-sampling Kriging model

同理根据上述方法，可以确定纵向最近距离阈值εymin、横向最远距离阈值εxmax和横向最近距离阈值εxmin，从而给出子级残骸概率安全区。

3 实例分析

以某型助推火箭子级残骸安全区计算为例，对提出的基于优化加点Kriging模型安全区预示方法进行仿真验证。子级残骸主要参数如表1所示，子级残骸分离时刻及飞行过程中主要偏差量分布规律如表2所示，为简便起见，不考虑风的影响。

表1 子级残骸主要参数Tab.1 Main parameters of booster rocket′s debris

表2 子级残骸主要偏差的分布规律Tab.2 Distribution regularity of booster rocket′s debris

3.1 与Monte Carlo方法对比分析

为了验证基于优化加点Kriging模型的安全区预示方法的快速性和准确性，首先采用Monte Carlo方法开展助推火箭残骸落点统计分析。取目标失效概率为Pfy1=Pfy2=Pfx1=Pfx2=0.01，为保证Monte Carlo采样点集相关系数小于0.05，根据式(15)计算出样本点个数约为40 000，则选取打靶次数为40 000对助推火箭残骸安全区进行统计。同时，取相同的目标失效概率，采用基于优化加点Kriging模型的安全区预示方法进行助推火箭残骸落点统计，两种方法对应的统计结果对比情况见表3。

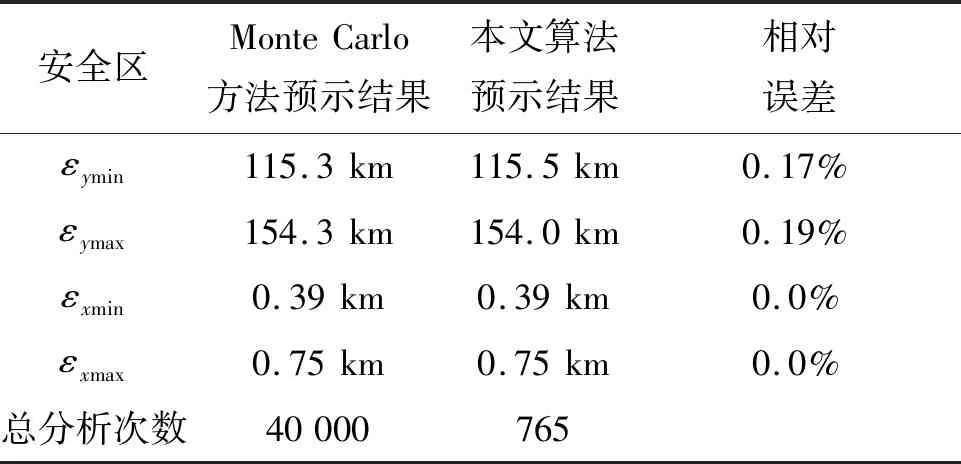
表3 两种方法计算结果对比Tab.3 Prediction result of two different methods

由表3可见，本文提出的基于优化加点Kriging模型的安全区预示方法与Monte Carlo方法相比，预示结果相对误差小于0.2%，具有较高的计算精度，且分析次数大大降低，具有较高的计算效率。

3.2 与极限偏差叠加方法对比分析

采用传统的极限偏差叠加方法，对助推火箭残骸分离时刻的相关偏差及残骸气动力系数偏差等进行极限偏差组合，计算出来的纵向最近距离εymin为100 434.8 m，纵向最远距离εymax为271 834.848 m，横向最近距离εxmin为243.995 m，横向最远距离εxmax为2214.77 m。对应的安全区预示范围与基于优化加点Kriging模型的安全区预示结果(失效概率阈值0.000 1)对比情况见图2。

图2 优化加点Kriging模型方法与极限偏差叠加法对比Fig.2 Prediction result of infill-sampling Kriging model and conventional extreme deviation overlying method

从图2可以看出，采用基于优化加点Kriging模型的安全区预示方法计算的安全区范围远远小于传统极限偏差叠加方法的安全区计算结果，前者面积仅仅是后者的13%，可大大降低发射场安全控制实施的难度。

此外，通过改变目标失效概率，可实现安全区的精细化预示，为发射场实施安全控制分级管理提供理论和数据支撑。图3中给出了失效概率阈值分别为0.1、0.01和0.000 1的助推火箭残骸安全区预示范围，对应的助推火箭残骸落点在该区域内的概率分别在60%、96%和99.96%以上。

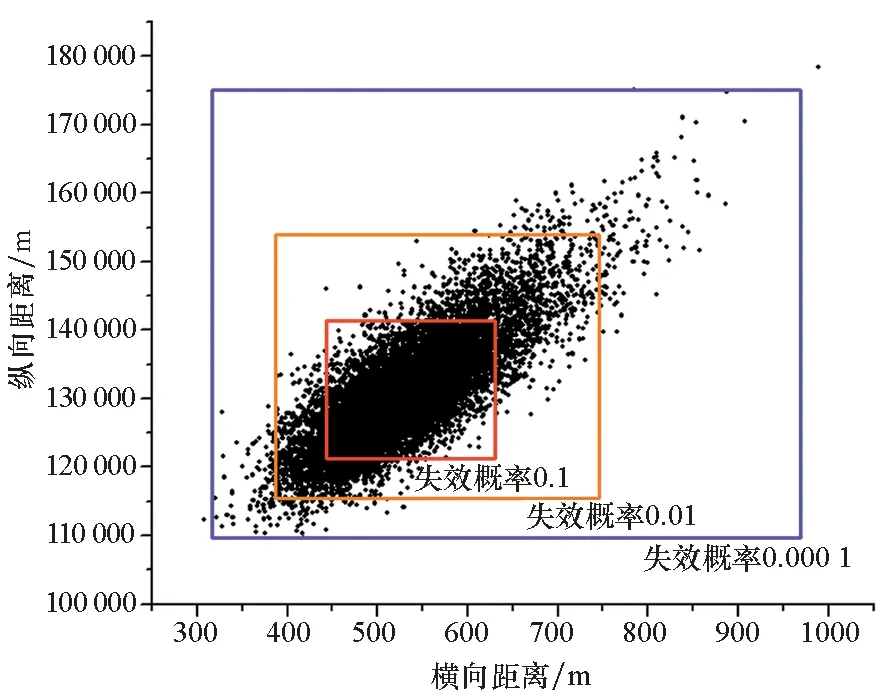
图3 不同失效概率对应的安全区预示结果Fig.3 Safety control zone prediction result under different failure probabilities

4 结论

本文的主要研究工作和结论如下：

1)建立火箭及其分离残骸弹道计算动力学模型，并采用四元数方法对姿态角解算进行处理；

2)提出基于优化加点Kriging模型的安全区预示方法，结合Monte Carlo和Kriging代理模型的特点，给出安全区预示流程；

3)以某型助推火箭残骸安全区计算为例进行仿真验证。结果表明，基于优化加点Kriging模型安全区预示方法具有较高的准确性和高效性，满足快速迭代的工程需求，相比传统极限偏差叠加方法，可显著降低安全区覆盖面积，具有较强的工程应用价值。