某型高速艇机有限元模态分析

孙浩俊，于洪亮，闫 锦，廖建彬

(集美大学轮机工程学院，福建 厦门 361021)

0 引言

游艇作为高端休闲产品，需要具有良好的舒适性，对振动也有更高地要求。游艇结构振动的振源主要来自主机的振动和海水对艇身的冲击等[1]，因此为了减小游艇艇身的振动，有必要研究如何降低柴油机工作所产生的振动。模态分析技术是现代机械产品结构动态设计和分析的基础，是近年来迅速发展起来的分析系统结构动态特性的强有力工具[2]。从分析方法的角度来讲，模态分析分计算模态分析和实验模态分析，用实验模态分析的结果来修正有限元模型，由此可得到精确的、合理的有限元模型。

Yuan G J等[3]建立了某型低速柴油机机体的有限元模型，通过计算得到机体的应力和位移分布，为机体结构优化提供了参考；Liu B等[4]利用有限元分析对S385柴油机机体进行了自由和约束模态有限元分析，通过对振动模态的分析，找出了机体的薄弱点，为改进机体的结构设计和动态响应分析提供了理论支持；李小雷等[5]建立了某大功率柴油机机体、曲轴、缸盖组合结构的有限元模型，为动力响应分析提供了参考依据；谭季秋等[6]采用有限元分析方法得到车用柴油机振动系统的固有频率和主振型，并与实验模态分析结果进行对比，最终得到可靠的柴油机计算模态分析结果。

本文以某型艇用柴油机为研究对象，建立了柴油机的三维几何模型和有限元模型，并进行有限元模态分析和实验模态分析，最后将有限元数值计算的结果和实验模态分析的结果进行对比，以验证有限元模型的合理性。

1 柴油机机体有限元模态分析

采用三维建模软件CATIA对柴油机机体和各个零部件建模，然后将柴油机整机几何模型导入ANSYS有限元分析软件中进行模态计算。

1.1 柴油机振动系统的模态参数求解

模态分析是进行结构动力学分析的基础，其最终的目标是获取结构的模态参数，即振动频率、模态振型和模态阻尼。在不考虑阻尼的情况下，结构的振动微分方程如式(1)所示[7]。

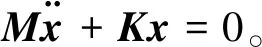
(1)

对式(1)进行求解，可以得到柴油机振动系统的固有频率和主振型。令式(1)的解为：

x=Xejωt。

(2)

式中：X是位移的幅值向量；ω为频率；t为时间。

将式(2)及其对时间的二阶导数代入式(1)，消去因子ejωt得：

(K-ω2M)X=0。

(3)

式(3)的特征方程可表达为：

det|K-ω2M|=0。

(4)

由式(4)可解得系统的固有频率ωi(i=1,2,…,n)，将ωi代入式(3)可求得对应的位移幅值向量X，即固有振型，并记为{φi}。

1.2 几何模型的建立

该柴油机为四缸直列四冲程小型艇用主机，净质量为300 kg，外形尺寸：长×宽×高=830 mm×664 mm×735 mm。

在建模过程中，综合考虑模型的精度和计算的时长，在构造计算模型时作适当的简化。不考虑直径小于5 mm的圆角，对影响不大的螺栓孔、水孔和油道孔等都不予考虑[8-10]。

图1为该型柴油机的实物图。

根据该柴油机机体的实际形状，在CATIA软件中建立对应的几何模型，如图2所示。

由于在建模过程中对机体及柴油机各零件进行了较多简化，最后建成的几何模型的质量要小于实际柴油机的净质量，二者质量的误差为4.93%。

1.3 有限元模型的建立

将几何模型导入ANSYS软件,建立有限元模型。模型各零部件所采用的材料和材料属性如表1所示。

在Design Modeler中将柴油机的某些零件组成一个多体部件，对不同材料的零件分别设置不同的材料，并且保证各个零件的网格彼此之间存在关联。

由于研究关注的是机体部分的模态，所以在进行网格划分时，将不影响柴油机机体模态振型计算的零件如活塞、连杆和附件等设置为刚体结构。这样不仅降低了网格划分的难度，减少了网格的单元节点数目，也减少了后续的模态分析的计算量。

选定Solid 187四面体单元对模型进行网格划分，网格单元尺寸为10 mm，单元总数为163 817个，节点总数为329 020个，具体划分情况如图3所示。

网格划分完成后，网格的平均质量(Average)为0.66，可用于有限元模态分析。

由于柴油机的4个底座都被螺栓固定于基座上，每个底座都被分别约束了3个移动自由度和3个转动自由度，所以应该对柴油机的4个支柱底部施加固定约束。采用Block Lanczos法进行模态计算。

表1 柴油机各零件所用材料及材料属性

1.4 有限元模态分析结果

对柴油机进行有限元模态计算，从计算结果中获得柴油机的前6阶模态振动频率和模态振型，如图4所示。

机体前6阶固有频率的计算值如表2所示。

表2 柴油机前6阶固有频率和模态振型

柴油机有限元分析得到计算模态的第1阶振型是油底壳的呼吸振动；第2阶振型是油底壳的1阶弯曲振动；第3阶振型是曲轴箱与油底壳连接处的呼吸振动；第4阶振型是曲轴箱与油底壳连接处的2阶呼吸振动；第5阶振型是机体绕曲轴轴线的扭转振动；第6阶振型是曲轴箱与油底壳连接处的2阶弯曲振动。

通过振型分析可知：柴油机机体和缸盖部分刚度较大，机体和缸盖部分振动的相对振幅很小；而油底壳和曲轴箱的刚度较小，发生在油底壳和曲轴箱上的振动的相对振幅比较大。该型柴油机的额定转速为3000 r/min，由额定转速计算得该柴油机的二谐次频率为100 Hz，远低于柴油机的第1阶模态频率，故机体与柴油机的激励不会发生共振。

2 柴油机机体的实验模态分析

对机体结构进行激振，考虑阻尼后，柴油机的振动方程为[11]:

(-ω2M+jωC+K)X=F。

(3)

式中：C为阻尼矩阵;F为激振力向量。

将位移向量X表示为互相独立的n组振动模态的线性叠加：

(4)

式中：γk(k=1,2,…,n)是振动模态坐标，取决于k阶振动模态的量。

将式(4)代入式(3)可得：

(5)

根据振动模态关于M、C、K的正交性，在式(5)两边同时左乘k阶振动模态φkT(k=1,2,…,n)，可解得k阶模态坐标γk，再由式(4)得

(6)

式中：mk、ck、kk分别为第k阶的模态质量、模态阻尼、模态刚度。

因为频响函数是响应和激励之比，所以由式(6)可以得到柴油机振动系统的频响函数为：

(7)

Hij表示在j点进行激励，在i点获取响应的频响函数。因为频响函数矩阵H是对称矩阵，Hij=Hji，为求得柴油机的振动模态，只需测量频响函数矩阵的一行或者一列即可。

2.1 实验方法和测试系统组成

采用脉冲激励法测试，给机体上单一点施加脉冲激励，在机体上多点同时采集响应信号。力传感器采集的力脉冲信号和加速度传感器采集的振动响应信号都是模拟信号，经过采集仪后转化为数字信号。对信号进行传递函数分析，将各测点的传递函数进行集总平均，确定该柴油机的低阶模态参数，并拟合出对应的模态振型。

模态测试现场如图5所示。模态测试系统原理图如图6所示。

2.2 测点布置与激振方案

考虑到该柴油机的外形特点和传感器安装的难易程度，在柴油机两侧的外壁各设置12个测点，总计24个测点。在柴油机的一侧安装12个三向加速度传感器，同时拾取振动信号。用力锤分别在柴油机的侧面、底部和曲轴轴向方向外壳上固定一点进行激振，三个方向激振完成后，重复上述步骤，对柴油机另一侧外壁的测点进行测试。为了测试结果的准确性，在每个激振点分别敲击5次。

2.3 模态测试结果

对每个测点的数据在LMS振动数据采集仪里进行频响函数计算，得到每个测点的频响函数，最后在LMS Test.Lab模态分析软件中对频响函数进行模态拟合，得到柴油机机体的前3阶固有频率，如表3所示。以实验模态的前3阶固有频率为基准，计算出计算模态与实验模态的固有频率的相对误差，其值小于3.02%，计算结果见表3。由表3可知建立的有限元模型是可靠的。

表3 机体试验模态振动频率

柴油机测试模态第1阶振型表现为油底壳的呼吸振动；第2阶振型表现为油底壳的1阶弯曲振动；第3阶振型表现为曲轴箱与油底壳连接处的呼吸振动。实验模态分析前3阶振型如图7所示。

3 结论

本文对一台艇用高速柴油机整机进行了计算模态和实验模态分析，得到如下结论。1)计算模态与实验模态振动频率相对误差小于3.02%，证明了经过适当简化的柴油机有限元模型可以被用来获取柴油机整机结构的动态特征。2)油底壳和曲轴箱处较大地振动会传输到游艇艇身，因此加强油底壳和曲轴箱的刚度，可以减少游艇的振动，提高游艇的舒适性。