西安市城市生活垃圾产生量的多元回归及ARIMA模型预测*

2020-05-09杨小妮张凯轩杨宏刚

环境卫生工程 2020年2期

杨小妮，张凯轩，杨宏刚，于媛

（1. 西安建筑科技大学华清学院，陕西西安 710043；2. 西安建筑科技大学环境与市政工程学院，陕西西安 710055；3.西安建筑科技大学资源工程学院，陕西西安 710055）

1 引言

2004 年起，我国超越美国成为世界第一大废弃物生产国，城市垃圾的管理已成为城市发展所要考虑的关键问题，生活垃圾产生量预测已经纳入城市环境卫生总体规划或城市环境卫生设施规划中。我国学者对城市垃圾产生量的预测做了大量研究：顾浩钦［1］利用灰色理论对上海市城市生活垃圾产生量进行了预测。熊蕾蕾［2］运用多元回归分析方法对徐州市2015—2022 年城市生活垃圾产生量进行预测。孙昊欣等［3］基于多元回归对无锡市城市生活垃圾年产生量进行了预测，但是没有对优选影响因子的过程进行介绍，直接选取了4个相关系数大于0.95 的影响因子。章清悦等［4］采用BP 神经网络对天津市2015—2017 年垃圾产生量进行预测。何鹏等［5］通过对各项预测方法特性的分析，选取灰色预测法，对天水市2017—2027年生活垃圾产生量进行预测，但是并未对垃圾产生量的影响因素进行定量的分析［5］。张红玉等［6］运用ARIMA 模型对北京市朝阳区的建筑垃圾进行了分析和预测。本研究运用ARIMA 模型预测已优选垃圾产生量影响因素，再利用多元线性回归模型对未来5 a 西安市城市生活垃圾产生量进行预测。

2 西安市城市生活垃圾现状

西安市2007—2016 年城市生活垃圾清运量见图1。江村沟是西安市最大的垃圾填埋场，目前90%的西安市城市生活垃圾存放在此，但以目前的垃圾产生量速率，预计2020 年将达到征地红线，不得不提前封场，西安市的城市生活垃圾处理问题已迫在眉睫。所以，科学、准确、合理地预测西安市未来几年的城市生活垃圾产生量，对做好城市生活垃圾日常控制工作、突发事件情况下的应急处置工作，以及城市规划管理有着重要意义。

图1 2007—2016 年西安市生活垃圾清运量

3 多元线性回归模型建立及预测

多元线性回归模型是研究在线性相关条件下，2 个或2 个以上自变量对一个因变量产生影响。而在城市垃圾产生量的预测分析中，对生活垃圾的影响因素有多项，受多个变量的影响。回归分析可以准确地计量各影响因素之间的相关程度与回归拟合程度的高低，做出优选提高预测方程的效果。所以多元回归分析法对生活垃圾产生量的预测更加方便和准确。

3.1 影响因素的选择

通常，影响城市生活垃圾产生量的主要因素为人口、经济发展水平、居民生活水平、基础设施建设水平4 个层面［7］。其中人口数量的增加必然会导致垃圾排放量的增加，随着西部大开发以及一带一路的建设，西安市作为整个西部的核心城市、丝绸之路经济带的起点，近年来涌入了一大批务工人员和技术人才，西安市的人口数量以及人口密度呈直线上升，同时，旅游接待人数也是影响城市垃圾产生量的一大重要因素。经济发展水平包括地区生产总值和社会商品零售总额。居民生活水平包括居民可支配收入、人均消费性支出和城市气化率/燃气率，但是西安市的城市用气普及率在2010 年已经超过99%，其对西安市未来垃圾产生量的影响很小，故本研究不再考虑将该因素作为未来西安市生活垃圾产生量的一个影响因素［8］。基础设施建设水平包括城区面积、清扫保洁面积、市容环卫专用车辆总数。表1 为2007—2016 年各影响因子数据［9］。

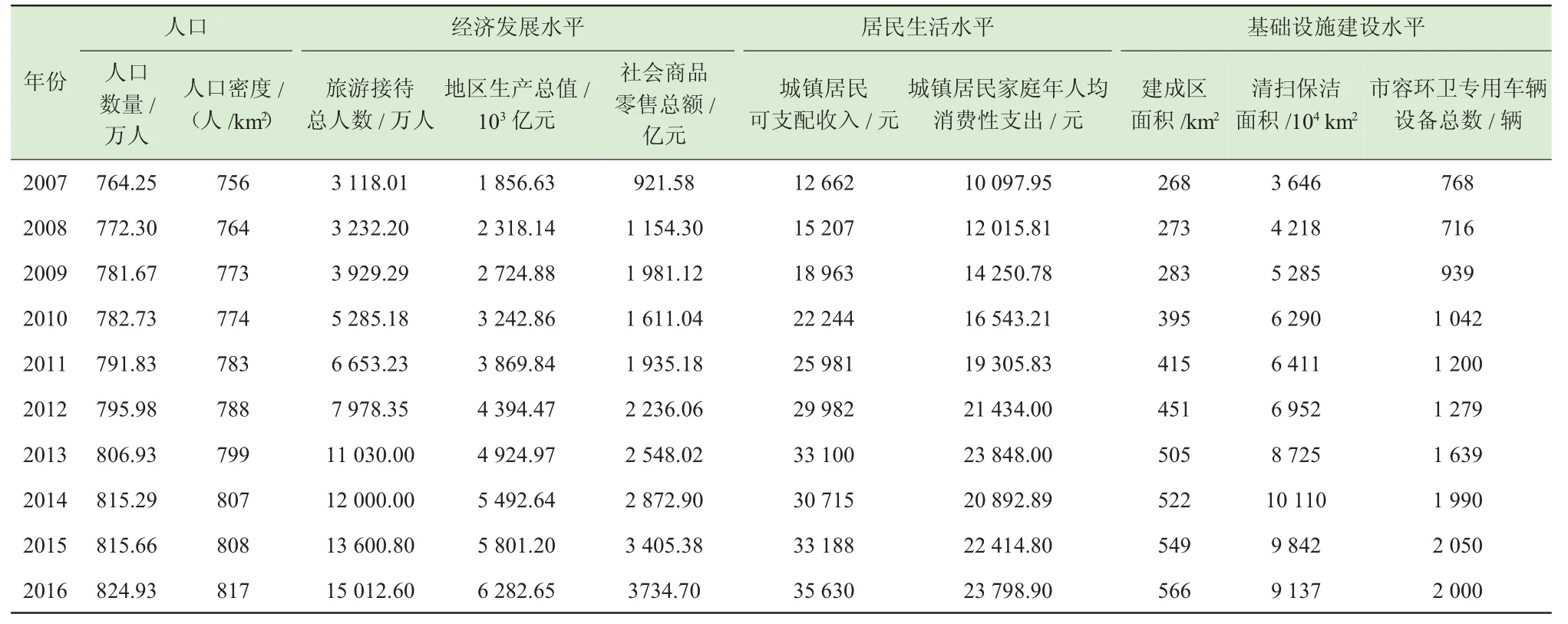
表1 2007—2016 年西安市生活垃圾产生量影响因素统计

为选取合适的影响因素，本研究通过对生活垃圾产生量和影响因子间关联系数进行计算，将其相关性进行量化比较从而得到最优选，计算方法如下：

式中：rm为y 关于zm的相关系数；zmi为第i 个历史数据对应的影响因子zm的数值；yi为第i 个历史数据对应的生活垃圾产生量，t；m 为选定影响因子个数；n 为有效历史数据个数，不应少于6 a，且应满足n≥m＋1，数据较为详实的地区宜使n≥3（m＋1）。

将表1 中各影响因子的数据作为建模数据，带入相关系数计算公式（1），得到表2 中影响因素与城市生活垃圾产生量的相关系数。

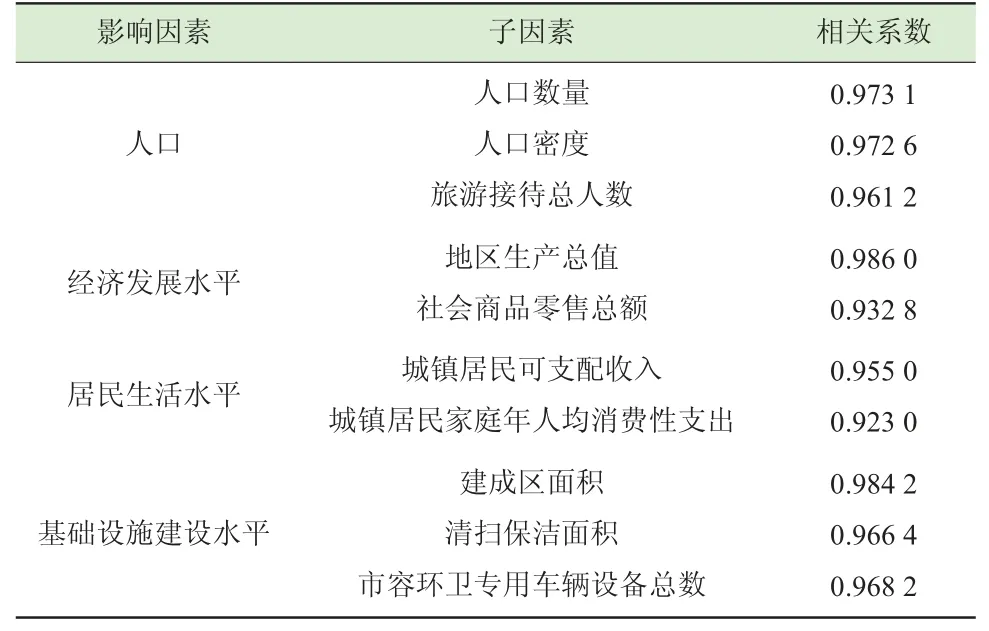
表2 西安市生活垃圾产生量与影响因素相关系数

从表2 可知0.973 1＞0.972 6＞0.961 2、0.986 0＞0.932 8、0.955 0＞0.923 0 及0.984 2＞0.968 2＞0.966 4，因此，在影响因子的选择中，人口中选择子因素人口数量，经济发展水平中选择子因素地区生产总值，居民生活水平中选择子因素城镇居民可支配收入，基础设施建设水平中选择子因素建成区面积。

选择影响因素时除参照关联度的分析结果外，还应考虑西安市城市规划及发展对各影响因素产生的影响。2019 年，西安市出台了最新的落户政策，不仅在政策上有所放宽，并且在经济上也做出了一定的支持，这让西安市人才引进计划得到了进一步发展，会对人口数量因素造成一定影响。而目前西安市已建成4 条地铁线路和1 条机场城际铁路，共计161.46 km，另有7 条在建项目，致使西安市内及其至各大城市间人员流动性大增，对经济状况有很大的刺激作用。上述情况对地区生产总值和城镇居民可支配收入均存在一定影响。同时，2019年，西安市安排棚户区改造在建项目30 个，总投资1 423.5 亿元，棚户区改造前期储备项目22 个，拟总投资1 173.5 亿元，两者累计棚户区改造项目52 个，这对建成区面积因素有较大影响［10］。综上所述，本研究中选择的4 个生活垃圾产生量的影响因素是合理的。

3.2 预测模型建立

假设获得n 组有效的历史数据（z1i，z2i，…，zmi，yi）（i=1，2，...，n），按式（2）构建多元线性回归分析模式对应矩阵模型：

式中：Y 为n 组生活垃圾年产生量有效历史数据的矩阵形式，即Y=（y1，y2，y3，…，yn）；Z 为n 组选定的影响因子有效历史数据的矩阵形式，

P 为回归系数的矩阵形式，即P=（p1，p2，p3，…，pm）。

利用选定的影响因子作为自变量Z，生活垃圾年产生量作为因变量Y，构建多元线性回归分析模型：

式中：P0，P1，P2，…，Pm为回归系数；Z1，Z2，...，Zm为各影响因子数据。

以2007—2014 年所选影响因素和生活垃圾年产生量为基础数据，带入公式（3）计算得回归系数P0、P1、P2、P3、P4，由此可得生活垃圾年产生量的预测模型：

式中：Z1表示人口数量，万人；Z2表示地区生产总值，亿元；Z3表示城镇居民可支配收入，元；Z4表示建成区面积，km2。

3.3 模型检验

将已知2015、2016 年所选影响因素数据分别带入公式（4），对2015、2016 年生活垃圾产生量进行预测并与实际垃圾产生量对比，从而对预测模型进行检验，具体误差结果见表3。

表3 西安市生活垃圾产生量多元回归模型误差检验结果

由表3 可知，预测的结果均大于实际值，且呈放大趋势，但是2 a 预测结果的相对误差均在20%以内。说明已建立的多元线性回归模型方法具备一定的合理性，但在预测未来5 a 及以上数据时，可能会存在误差大的缺点，建议该模型在应用时只针对未来4 a 内的结果进行预测。

3.4 西安市城市生活垃圾产生量预测

由于运用多元线性回归方程对生活垃圾产生量进行预测，需要所预测年份的对应4 个影响因素的影响数据，故引入ARIMA 模型对2019 和2020 年各影响因素的数值进行预测。

ARIMA 模型，也称为著名的Box-Jenkins 模型，是由Box 和Jenkins 在70 年代初创立的一种时间序列建模方法。一个ARIMA （p，d，q）模型就是一个作了d 次差分后的ARIMA （p，q）模型，而ARIMA （p，q）是AR（p）和MA（q）的组合。针对常见的非平稳时间序列，通过差分的方式，变为相对平稳的时间序列。d 为时间序列成为平稳时所做的差分次数，代表时序数据需要进行几阶差分后才是稳定的。AR 是自回归，p 为自回归项，一般代表预测模型中采用的时序数据本身的滞后数；MA 为移动平均，q 为移动平均项数，代表预测模型中采用的预测误差的滞后数［11-12］。

1）阶数为p 的AR 模型的算法方程如下：

式中：yt表示样本值；φi（i=1，2，…，p）表示AR（p）的参数，αt表示白噪声序列。

AR 模型反映的是当前t 时刻的样本值yt，与前t-1 时刻的值yt-1，前t-2 时刻的值yt-2，直到前p 时刻的值yt-p之间的线性关系。

2）阶数为q 的MA 算法方程如下：

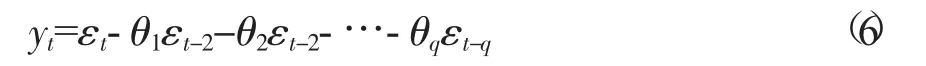
式中：yt表示样本值；θi（i=1，2，…，q）表示MA（q）的参数；εt表示白噪声。

MA 体现的是t 时间点的样本值yt与q+1 个不同时间点的噪声的关系。

3）一个ARMA（p，q）过程可以视为AR（p）与MA（q）过程的迭加，模型结构如下：

式中：yt表示样本值；φi（i=1，2，…，q）和θi（i=1，2，…，q）表示ARMA（p，q）的2 个参数；εt表示白噪声，且εt～N（0，σ2）。

ARMA 体现的是t 时间点的样本值yt，和前p个不同时间点的值以及q+1 个不同时间点的噪声的关系。

3.4.1 影响因素的ARIMA 预测

1）数据平稳性的检验。ARIMA 模型建模的基础是要确保数据的平稳性，即数据随时间序列在某一常数值间随机在一定范围内波动，本研究采用自相关图法进行检验。

2）数据平稳性处理。采用一阶差分法对非平稳化数据进行平稳化处理。

3）模型定阶。以人口数量这一影响因素为例，利用AIC 准则确定最佳模型阶数为p=2，q=1，d=1。

4）模型参数估计。在MATLAB 的库函数中调用最小二乘法对模型参数进行估计。

5）残差白噪声检验。合适的ARIMA 模型尽量拟合线性成分，残差表现为白噪声。可对残差进行Q（Ljung-Box）统计量和自相关图分析。检验的结果就是看检验概率p 值。本研究中显著性水平取为0.05。如果检验概率p 值大于给定的显著性水平，就拒绝原假设（其原假设是相关系数为零），即序列为白噪声。LB 检验结果见表4，表4 中人口数量、地区生产总值、城镇居民可支配收入、建成区面积前1～8 阶的p 值都显著大于0.05，说明相关系数与零没有显著差异，即时间序列中有用的信息已经被提取完毕，残差数列为白噪声，故建模成功。