基于频域中值滤波的自适应卫星通信恶意干扰检测

刘建成,郝学坤,王赛宇,王 超,姜少飞

(1.中国电子科技集团公司第五十四研究所,河北 石家庄 050081;2.中国电子科技集团公司第五十研究所,上海 200331;3.中国人民解放军31634部队,云南 昆明 611731)

0 引言

信息化战争已是目前军事活动的主要形式，伴随而至的是作战双方围绕电磁信号的对抗升级。对于应用战略重要性日益突出的卫星通信而言，将面临严重的敌方实施的恶意干扰，抗干扰技术方法已成为保障可靠通信必不可少的措施，而干扰有效检测是进行抗干扰的前提和基础，所以如何有效检测接收信号中是否存在干扰已成为抗干扰卫星通信所亟待解决的问题。

目前，针对人为恶意干扰的检测方法主要可分为能量检测、循环平稳特征分析和高阶累积量计算三方面。能量检测法可在时域和频域进行，频域能量检测通过对信号频谱能量统计分析实现，具有一定的抗噪能力，应用更为广泛。文献[1]针对常规能量检测法易受外界噪声影响的问题，研究利用背景噪声的估计强度设定检测门限，一定程度上提升了能量检测法的性能。文献[2]针对典型的能量检测算法，研究了该算法在多径衰落和遮挡信道条件下的检测性能，推导了对应的检测概率和虚警概率数学表达式，为能量检测算法的应用提供了理论依据。文献[3]在原有能量检测基础上，提出双门限检测法，即根据接收信号噪声的强度大小分别设定两个检测门限，以实现不同噪声强度情况下的窄带干扰检测，弥补了低信噪比时能量检测法的不足。文献[4]将改进的能量检测算法应用于同时收发认知抗干扰通信系统，通过频谱感知阶段获得的自扰信道容量与系统传输速率比较，分别设定不同的门限进行能量检测。

对于循环平稳特征分析的检测方法[5]，主要是利用了信号的循环平稳特征以及相关特性，区分干扰信号与噪声。文献[6]针对卫星通信系统干扰检测问题，首先分析了能量检测和信号功率谱密度估计算法，进而设计基于Welch谱估计和能量检测相结合的干扰检测方法。文献[7-8]针对雷达面临的宽带压制式干扰，研究了宽带干扰的数字互相关检测方法，并对其性能进行了理论推导和分析，该检测方法需要两个接收站获得不同时延不同方位的信号，进行互相关处理。文献[9]研究认知无线电的频谱感知方法，对OFDM信号进行符号周期内的循环自相关函数估计，同时计算判决门限，并进行比较判断有无信号。

由于二阶矩构成的特征只能针对具有平稳特征的信号，研究者们提出了高阶累积量的分析方法，并应用于信号检测。文献[10]研究低信噪比条件下的信号检测问题，提出了基于四阶累积量的DSSS/QPSK信号检测方法，利用信号非平稳特征克服了环境噪声对检测性能的影响。文献[11]针对全球导航卫星系统(GNSS)强噪声条件下干扰检测问题，研究基于高斯噪声三阶对角切片的高阶累积量检测方法，该方法是利用高斯噪声三阶以上累积量近似为0的特性，实现抑制噪声检测干扰的目的。文献[12]指出能量检测和循环平稳特征分析检测只适用于平稳噪声环境，为此提出基于四阶累积量(循环多谱)的感知算法，能够有效实现非平稳噪声环境的频谱感知。

除上述3种典型干扰检测方法外，研究者们还针对某些特殊场景提出了不同的检测方法。文献[13]针对直扩通信系统中的窄带干扰，利用压缩采用情况下的特征量实现了窄带干扰有效检测，不过其检测性能随干扰带宽增大和强度的减弱而产生明显恶化。文献[14]以码分多址测控系统为研究对象，提出变换选择模式识别的干扰检测方案，该方法对脉冲干扰、调频干扰和窄带干扰分别采用压缩增益和谱均值-方差进行检测，检测过程需要进行分数阶傅里叶变换，计算复杂度较高。文献[15]针对直接序列扩频系统，研究利用不含干扰的接收信号特征实现对复杂干扰的检测，该方案对传输帧和同步前缀的形式有特定要求，不适用于其他系统。文献[16]利用GNSS信号时延特征，给出了针对转发式欺骗干扰的信号捕获阶段的联合检测方案，该实现方案主要采用多峰与半高宽检测判断有无转发式欺骗干扰。文献[17]针对不同调制方式对应的最优干扰，采用匹配滤波比较的方法实现混合信号有无最优干扰的判断，该检测方案需要多组匹配滤波器，检测干扰的样式受限。文献[18]针对多天线认知无线系统，研究提出基于协作分散自适应的特征值频谱感知方法，有效提升了多天线系统的频谱感知能力。文献[19]针对认知无线电系统频谱感知所面临的射频干扰，利用循环谱分析和人工神经网络实现了基于压缩感知的宽频带干扰检测，不过该检测方法针对性强，且实现较为复杂。

综上所述，循环平稳特征分析和高阶累积量检测方法计算复杂度高，对待检测的恶意干扰类型有特殊要求，而现有能量检测方法具有抗噪能力弱和适应性差的不足。为此，本文提出基于频域中值滤波的自适应恶意干扰检测方法，具有计算复杂度低、易实现和噪声环境适应能力强的特点。

1 频域中值滤波自适应干扰检测

干扰的能量检测法具有简单易实现的优点，在实际中得到了充分应用。但是由于干扰检测需要同时考虑期望信号和噪声的影响，能量检测法采用相对固定的判决门限，使其对噪声环境和期望信号的适应能力较弱，降低了检测性能。

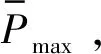
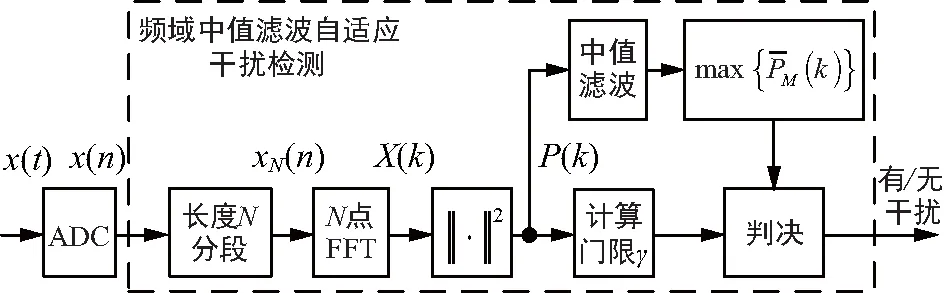
图1 频域中值滤波自适应干扰检测原理框图Fig.1 Principle of adaptive jammer detection based on medium filtering in frequency domain

将接收信号x(t)采样值x(n)进行长度为N的分段处理，得到序列xN(n)，再进行N点FFT变换：

(1)

对FFT序列X(k)求模的平方并进行修正，使得中心频率对应为k=N/2，表示为：

P(k)=SHIFT{‖X(k)‖2}。

(2)

(3)

同时，依据设定的采样率fs和待检测带宽B，确定带宽B对应P(k)中的数据个数M，记带宽B对应的数据为PM(k)，M和PM(k)计算如下：

(4)

(5)

式中，门限计算时的调整系数α需要考虑实际的期望信号强度与噪声强度，其原则为低信噪比时α应取值偏大(为保证小的虚警概率，通常设置其上限为2)，而随着信噪比的增加α逐渐减小至1。这主要是因为，当信噪比较小时，噪声的随机性会增加检测的虚警概率，需将门限计算的调整系数α增大;而随着信噪比的增大，噪声影响逐渐减弱，门限调整系数α应该减小以提升低干信比情况下的成功检测概率。

可见，频域能量检测实现简单，具有抑制噪声能力。在非静默期干扰与期望通信信号、噪声同时存在的情况下，当干扰信号带宽小于通信信号带宽的1/2时，通过本文提出的频域中值滤波法能够有效检测是否存在干扰。若干扰与通信信号带宽相当，二者在频域几乎重合，则需进一步采用其他特征进行干扰检测。

2 性能分析

干扰检测方法性能优劣体现在检测概率Pd与虚警概率Pf，以及方法实现的计算复杂度，所以该节将推导分析本文干扰检测方法的检测概率、虚警概率及其计算复杂度。

对于干扰检测是二元判定问题，即将计算的变量与设定的门限对比，得到有无干扰的结果。由帕塞瓦尔定理[20]可知，傅里叶变换之后并不改变信号强度大小，便于分析可将检测概率推导转换至时域。对于干扰检测，其时域数学表述为：

(6)

式中，j(t)为干扰信号，n(t)表示外界噪声。为便于分析，同时不失其一般性，n(t)可认为是均值为0、方差为σ2的加性高斯白噪声。

(7)

由于检测变量Ep中的期望信号和干扰强度是确定的，且期望信号与噪声、干扰与噪声、期望信号与干扰之间均可认为是不相关的。假设期望信号为强度为ps，干扰强度为pj，对有无干扰2种情况下，变量均值计算如下：

(8)

考虑期望信号可认为是幅度恒定的信号，根据式(8)计算检测变量方差时可略去期望信号的强度分量，计算如下：

由大数中心极限定理[20]可知，当检测判决点数足够多，检测变量将服从正态分布，其均值和方差如式(8)和式(9)，故可推导得出检测概率与虚警概率表达式为：

(10)

除检测概率外，算法计算复杂度也是影响其实际应用的重要因素。本文提出的检测方法以FFT为基础，假设接收混合信号数据长度为N，中值滤波长度为L，则除FFT运算外只需(N-2L)L次加法运算，而通常情况下N远大于L，所以本文检测方法的计算复杂度与常规频域能量检测算法在同一数量级，并未显著增加计算量。

3 仿真验证

由于实际应用中，卫星通信载荷或地面终端接收的待检测信号通常包含通信信号、干扰信号和信道环境噪声，故本节仿真考虑通信信号与干扰并存的非静默期场景，仿真对比不同信噪比和信干比情况下本文方法与典型频域能量检测[2]。

仿真以单音、多音、线性调频和部分频带噪声4种典型恶意干扰为检测对象，期望信号假设为QPSK，其符号速率R为1.28 Msps。同时考虑卫星通信传输信道多径效应弱等特点，可初步考虑采用高斯白噪声信道，干扰具体仿真参数设置见表1。本文方法与典型频域能量检测方法的FFT点数均为1 024，本文方法中值滤波长度L设为100，门限调整系数α为1.15，典型频域能量检测方法判决门限设为检测带宽内平均能量的1.25倍。统计1 000次蒙特卡洛仿真，得到不同SNR和不同ISR对应的检测率，期望信号带内SNR设为3 dB和10 dB，干信比ISR从-20～10 dB。SNR为3 dB时两种干扰参数对应的仿真结果如图2所示，SNR为10 dB时2种干扰参数对应的仿真结果如图3所示。

由图2结果可见，在期望信号与信道噪声功率之比为3 dB时，对于仿真所采用的4种典型干扰，本文提出的检测方法性能均优于已有的频域能量检测算法。以单音干扰为例，当检测概率为80%时，本文方法与典型频域能量检测算法相比，所需干信比JSR降低约4 dB，而其他3种干扰的性能提升均在5 dB以上。对比图2(a)和图2 (b)可见，当干扰参数发生变化，即扫频干扰和部分频带噪声干扰的带宽变大时，已有的典型频域能量检测算法对扫频和部分频带噪声干扰的检测性能急剧下降，当JSR高达10 dB时，仍无法实现有效检测，而本文方法检测概率仍能达到90%以上。分析图3(a)和图3(b)，可见其变化趋势与图2基本一致，本文提出的检测方法性能提升显著。

表1 几种干扰参数设置
Tab.1 Parameters of jammers

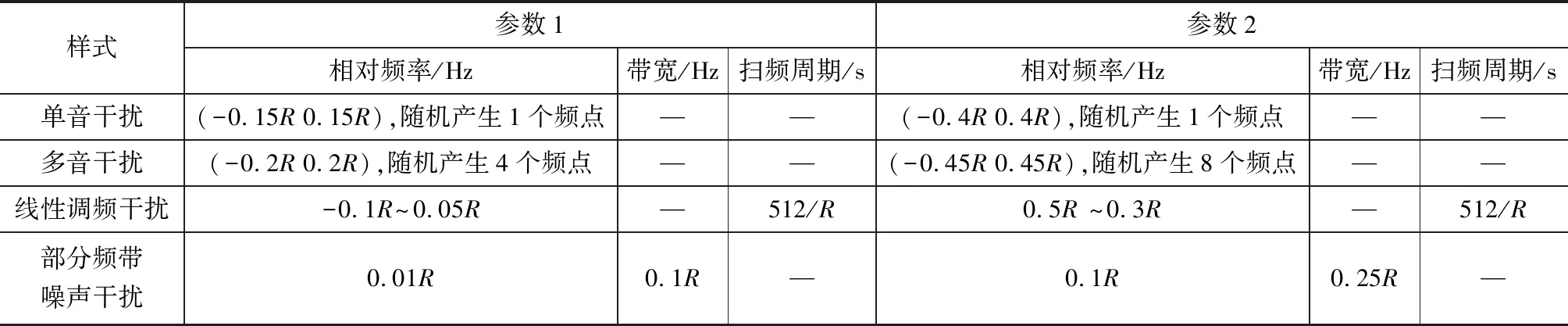
样式参数1参数2相对频率/Hz带宽/Hz扫频周期/s相对频率/Hz带宽/Hz扫频周期/s单音干扰(-0.15R 0.15R),随机产生1个频点——(-0.4R 0.4R),随机产生1个频点——多音干扰(-0.2R 0.2R),随机产生4个频点——(-0.45R 0.45R),随机产生8个频点——线性调频干扰-0.1R～0.05R—512/R0.5R ～0.3R—512/R部分频带噪声干扰0.01R0.1R—0.1R0.25R—

图2 SNR=3 dB时2种干扰参数的检测概率曲线Fig.2 Detection probability curves of two parameters with SNR=3 dB

图3 SNR=10 dB时2种干扰参数的检测概率曲线Fig.3 Detection probability curves of two parameters with SNR=10 dB

另外，对比图2和图3可发现，由于SNR的增大使得信道噪声对检测性能的影响减小，本文方法和已有检测算法对干扰的检测性能均有所提升。尤其是对于参数(2)对应的扫频和部分频带噪声干扰，当SNR由3 dB增加至10 dB，本文方法在JSR为5 dB时，检测概率已能够达到95%以上，已有方法在JSR为10 dB时检测概率也提升至80%左右。

由此可见，对于不同类型的干扰，在不同信道环境条件下，本文提出的干扰检测方法与典型频域能量检测算法相比，性能均有较大改善，能够有效实现恶意干扰的准确检测。

4 结束语

针对卫星通信在军事应用中面临的恶意干扰检测问题，提出了基于频域中值滤波的自适应恶意干扰检测方法。通过不同信道条件下对典型恶意干扰检测的仿真对比，表明本文提出的方法能够显著改善检测性能，所需干信比降低5 dB以上。同时理论分析表明，该方法具有低计算复杂度，便于实现。综上所述，本文提出的基于频域中值滤波的自适应恶意干扰检测方法，能够显著改善现有能量检测算法的性能，实现不同条件下多类型相对窄带干扰的有效检测。