基于空间网格模型的装配式钢板组合梁桥受力分析

曾思清，杨 凯，王伟力，杨大海

(1.广东云茂高速公路有限公司，广州 510623；2.安徽省交通规划设计研究总院股份有限公司，合肥 230088)

0 引言

随着国家政策的引导与产业技术的发展，近年来装配式桥梁应用逐渐增多。装配式桥梁的主要特点在于设计标准化、生产工厂化与安装机械化。在中小跨径的桥梁建设中，选择使用组合结构具有较好的经济效益与技术优势，是实现中小跨径桥梁装配化的一种较优途径。双主梁钢板组合梁桥具有构造简单、受力明确、用钢量较低、施工方便等优点，目前在国内多个省份已有应用。工字型主梁与桥面板均采用工厂预制，两道工字梁间通过小横梁连接形成框架。预留湿接缝与桥面板剪力钉槽，通过后浇混凝土实现与钢主梁结合，桥面板通过预留剪力钉槽与钢主梁结合成组合截面，小横梁和桥面板无连接。其典型构造如图1所示。

图1 装配式双主梁钢板组合梁桥典型构造

在高速公路的桥梁建设中，双主梁钢板组合梁桥面板宽度适用范围一般在12.25m～16.75m，主梁间距一般为桥面宽度的0.55倍；其主梁间距和桥面板宽度均较大，所以受力区别于“浅窄梁(全截面的变形满足平截面假定、构件的剪应力按开口截面的弯曲应力取用、忽略顶板的水平剪应力)[1]”，具有明显的空间效应。桥面板承受纵桥向正应力、横桥向正应力与面内主应力，存在比较突出的剪力滞效应。在2018年实施的《公路钢筋混凝土及预应力混凝土桥梁设计规范》(JTG 3362-2018)中提出一种精细化分析方法—空间网格模型[3]。文献[1-2]对混凝土箱梁采用空间网格的精细化分析方法进行了研究，并于实体模型进行对比。文献[4]提出采用空间网格法模拟波形钢腹板组合梁桥，对空间网格划分密度与计算精度进行了研究。文献[5]采用空间模型对组合梁斜拉桥进行承载能力分析。根据双主梁钢板组合梁桥的结构与受力特点，其适用于精细化的空间网格模型，但针对空间网格模型在装配式钢板组合梁桥中的应用尚未见文献研究报道。

本文以某双主梁钢板组合梁桥为工程实例，采用平面梁格法、空间网格模型、实体板壳有限元分析模型，对比3种分析方法的基本原理与计算结果，以验证空间网格模型在组合梁中应用的有效性与可靠性。

1 工程实例

以某一装配式钢板组合梁桥为工程实例，取一标准联(3×30m)进行分析。钢主梁的梁高为1.6m，桥面板的宽度为12.75m，桥面板横向张拉预应力，标准断面如图2所示。主梁钢材为Q345qD，预制桥面板混凝土等级为C50，湿接缝为无收缩微膨胀混凝土。根据建造条件和建造规模，钢梁的架设可选择顶推施工、汽车吊施工或架桥机施工。施工的主要流程：架设钢梁→吊装桥面板→浇筑剪力钉槽与湿接缝→桥面铺装与安装护栏。根据施工流程可知，桥面板与钢梁自重由钢主梁独自承担，二期荷载与运营活载由组合梁截面承受。

图2 标准断面(单位：mm)

2 分析模型

2.1 平面梁格模型

平面梁格模型是将结构用一个梁格来等效模拟，真实结构的纵向刚度等效为纵向梁格刚度，横向刚度等效为横向梁格刚度[2]。平面梁格模型能能够计算腹板受力分配效应，但在计算薄壁效应和剪力滞效应时存在不足，荷载的横向传递通过横向梁格进行分配，可以解决腹板剪力计算问题，但不能计算桥面板内的面内剪应力与主应力。

本文的计算模型根据工字型主梁位置，将结构划分为两道纵梁，桥面板与钢梁的组合作用通过MIDAS CIVIL中组合截面实现；两道纵向主梁直接通过横向梁格连接。其有限元离散模型如图3所示。

图3 梁格法计算模型

2.2 实体与板壳模型

实体与板壳模型能够较真实地对几何、荷载、边界进行模拟，可以考虑腹板受力分配效应、薄壁效应、剪力滞与局部荷载效应[1]；但计算模型的分析结果包含了整体效应与局部效应，两类效应难以区分，且内力需要根据应力积分得到。

本文的计算模型利用土木专用的有限元分析软件MIDAS FEA进行分析，桥面板采用六面体实体单元，钢梁采用四节点板单元，预制桥面板和钢梁上翼缘之间的连接通过共节点的方式实现。

图4 实体与板壳模型

2.3 空间网格模型

空间网格模型是将结构离散成板单元，每一块板单元被离散为十字型交叉的正交梁格，用该十字交叉的纵横梁格等效替代板的刚度[5]。空间网格模型需要根据结构形式、受力特性与施工方案进行截面离散与划分。截面离散与划分后，结构的整体受力转化为各“划分梁”的受力，例如截面弯矩转化为顶板和底板划分梁的轴力，受力模式与板壳模型基本类似。

在本文的空间网格计算模型中，根据装配式钢板组合梁桥的结构特点与施工流程，将组合梁结构中的钢梁和混凝土板离散，如图5所示。由于工字梁上下翼缘宽度较小且腹板受力满足平截面假定，因此工字型钢梁采用单梁进行模拟；根据剪力钉布置数量，桥面板与钢梁之间属于完全抗剪连接，因而通过刚臂连接钢主梁和混凝土桥面板单元。本文计算重点关注桥面板的空间效应，桥面板采用十字交叉的正交梁格进行模拟，如图6所示。通过计算，可以得到各正交梁格截面的内力。

图5 截面离散

图6 桥面板简化原理

3 结果分析

3.1 静力分析对比

根据前述所建立的分析模型，提取二期恒载作用下的桥面板上缘纵桥向截面正应力。表1为空间模型计算所得中跨跨中截面与中支点截面桥面板应力，空间网格模型准确反映出桥面板的剪力滞效应。将空间网格所得结果与平面梁格模型、实体板壳模型进行对比。从图7与图8可知，利用空间网格模型计算得到的桥面板截面纵桥向应力分布为阶梯状，其计算结果与实体板壳模型分析基本一致，相对差值基本保持在5%以内，最大相差在9%(约束位置)，说明空间网格模型满足工程精度需求。

表1 空间网格模型桥面板纵向应力

注：表中正值为压应力，负值为拉应力。

图7 跨中截面桥面板应力对比

图8 支点截面桥面板应力对比

相比于平面梁格法模型，实体板壳模型与空间网格模型均可得到结构不同位置处的位移。为研究空间网格模型的位移计算精度，在第2跨满布车道荷载，集中荷载作用于跨中，提取空间网格模型中9号梁活载下的位移，并与实体板壳模型相应位置的位移(图9)进行对比(图10)。空间网格模型与实体板壳模型最大竖向位移均发生在跨中，空间网格模型最大竖向位移为3.26mm，实体板壳模型为3.48mm，两者相对差值为6%，其他位置位移相对差值在3%左右。空间网格模型的位移计算精度较高，能够实现结构分析的精细化要求。

图9 实体板壳模型桥面板位移(单位：mm)

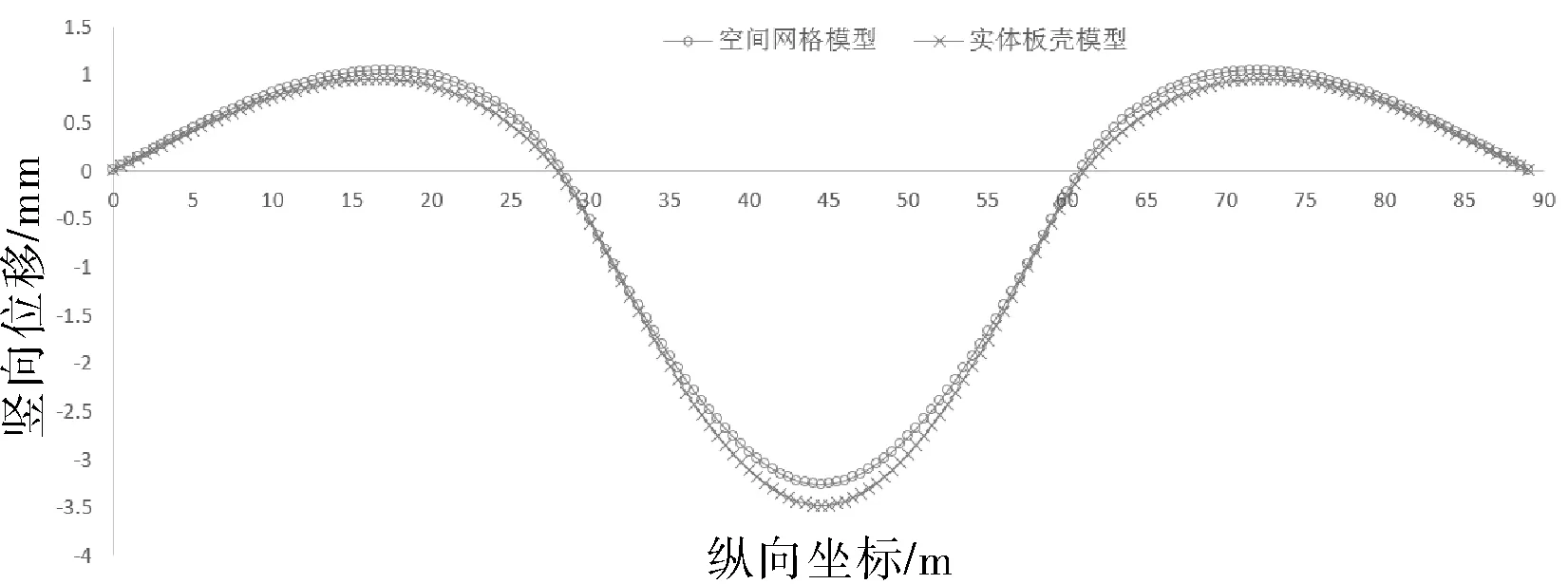
图10 桥面板相同位置位移对比

3.2 动力特性分析

自振频率与振型是结构自身动力特性的直接反应,本文对3种计算模型的前5阶振型与自振频率进行对比研究。图11为3种计算模型的一阶振型模态，均为竖弯振型。表2中对3种计算模型的前5阶自振频率进行对比，平面梁格模型和实体板壳模型的计算结果相对误差在2%～15%之间，空间网格模型与实体板壳模型的计算结果相对误差在10%以内；同一模态相比，空间网格模型计算结果与实体板壳模型更接近。通过以上分析对比，表明采用空间网格进行计算，其对结构的刚度与质量分布模拟更接近实际情况。

图11 一阶振型模态

表2 自振频率对比

4 结论

本文通过对某一装配式双主梁钢板组合桥梁的计算分析，对比平面梁格模型、空间网格模型与实体板壳模型的静力与动力计算结果进行对比，主要得到以下结论：

(1)空间网格模型适用于钢板组合梁桥的静力计算分析，其截面应力分布与位移的计算结果和实体板壳模型计算结果一致，能准确反映结构的空间受力特性。

(2)空间网格模型适用于动力计算分析，相比于平面梁格模型，其能较准确地模拟结构的刚度与质量分布。

(3)实体板壳模型虽然精细化程度较高，但建模难度较大，计算速度较慢。空间网格模型弥补了平面梁格模型的不足，同时建模相对简单且计算效率较高，是一种适用于工程实际的精细化分析模型。