基于边界分析的最大实体要求和最小实体要求混合设计与标注

徐旭松，吴德辉

(1.江苏理工学院 机械工程学院，江苏 常州 213001； 2.浙江省先进制造技术重点实验室，浙江 杭州 310027; 3.博世电动工具(中国)有限公司，浙江 杭州 310052)

0 引言

Requicha[3]提出以实效边界为基础研究含公差信息的CAD几何模型和计算机辅助公差设计方法。为了将公差标准中的不易操作的语义和图示形式的公差带实用化，Jayaraman等[4-5]提出了用于公差描述的实效边界要求(Virtual Boundary Requirements, VBRs)和状态公差(Conditional Tolerances, CTs)的概念。Dantan等[6]在上述构想和理论的基础上，采用实效边界来表达产品装配与功能的状态，提出了“体内可迁移”的虚拟量规的概念来约束零件的几何变动，并以此虚拟量规来验证MMR和LMR。Pariel等[7]提出了使用最大实体和最小实体要求的“虚拟配合量规”的概念模型，并研究出将其运用于尺寸计量的具体算法。Humienny等[8]采用动画技术，对垂直度和位置度公差标注中的最大实体要求应用于被测要素和基准要素时的公差补偿和基准偏移进行了可视化研究。Anselmetti等[9-10]基于实效边界分析和虚拟量规研究了最大实体要求和最小实体要求在功能公差设计中的应用和标注，特别是针对复杂装配节点公差设计中的应用及复杂曲面的最大实体要求/最小实体要求使用、补充定义、标注方法，完善了GPS标准，并指出最小实体要求在工程中应用未得到充分调研，其在工程中的价值仍未引起足够重视和广泛研究。国内学者杨将新等[11]研究了基于最大实体要求和最小实体要求的同轴度公差数学模型。茅健等[12]将小位移矢量簇引入到公差数学建模中，系统地研究了轴/孔位置度公差在最大实体要求和最小实体要求下的不同约束条件及相应的位置度公差数学模型。潘淑清[13-14]探讨了相关要求在结构设计中的应用，并对零件采用相关要求的评定方法进行了研究，李丽娟等[15]研究了采用最大实体要求、可逆要求下零件的合理评定方法。吴玉光等[16]研究了对基准要素采用最大实体要求时的几何要素检验方法。黄美发等[17]研究了被测要素和基准要素使用最大实体要求的M-M同轴度误差数学模型及评定方法。

综上所述，最大实体要求在公差控制中的运用已得到广泛研究，相对而言，最小实体要求在公差设计中的运用未得到广泛重视和应用。本文在已有文献研究的基础上，以某铰链组件公差设计为例，利用实效边界分析方法研究最大实体要求和最小实体要求在被测要素和基准要素上的应用及其混合标注。

1 实效状态边界

边界(Boundary)是由设计给定的具有理想形状的极限包容面(极限圆柱面或两平行平面)。该极限包容面的直径(或距离)称为边界尺寸。当最大实体要求或最小实体要求应用于几何公差规范时，就形成状态公差，此时的公差带边界形成实效状态边界(Virtual Condition Boundary, VCB)，零件的实际要素(提取组成要素)不得超出实效状态边界。实效状态边界反映几何功能要求，其本身就是相对于基准或基准系的一个理想几何要素，它具备几何要素的4大特征(大小、形状、方向、位置)。实效边界要求有2种类型[4-5,18]：①装配要求；②材料体积要求。装配要求是对零件材料增加量的限制；材料体积要求是对零件材料减少量的限制。实效状态边界(VCB)是尺寸公差和几何公差共同形成的边界，实际要素(提取组成要素)全部位于装配要求或材料体积要求的实效边界之内则认为满足功能要求，零件合格。例如，几何公差规范到尺寸要素上、并使用最大实体要求，这将在尺寸要素的实体外部(非材料边)附近形成一个实效状态边界，即最大实体实效边界(Maximum Material Virtual Boundary, MMVB)，实际要素不得跨越最大实体实效边界；而当使用最小实体要求时，将在尺寸要素的实体内部(材料边)建立起一个实效状态边界，即最小实体实效边界(Least Material Virtual Boundary, LMVB)，实际要素不得跨越最小实体实效边界[19]。实效状态边界计算见表1。

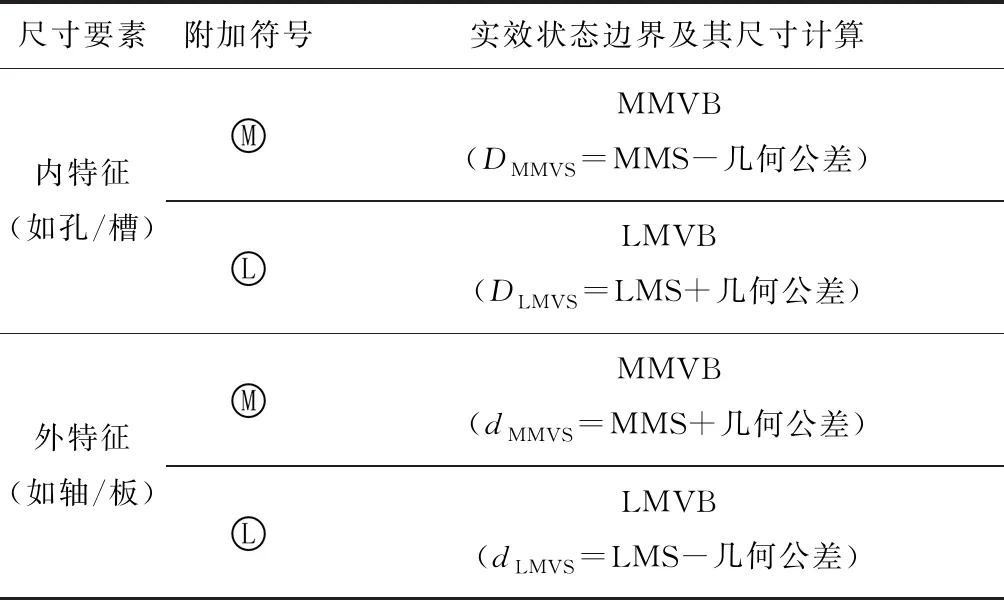
表1 实效状态边界及计算

最大实体要求(最小实体要求)是指提取组成要素应遵守最大实体实效边界(最小实体实效边界)，且局部尺寸应处于极限尺寸之内。最大实体要求(最小实体要求)适用于导出要素(中心要素)有几何公差的综合要求的情况。最大实体要求和最小实体要求既可用于被测要素，也可用于基准要素。

2 最大实体要求应用于被测要素与公差补偿

2.1 最大实体要求应用于被测要素实例分析

如图1所示的铰链结构组件装配，它由上板、下板、铰链销和挡圈组成。装配过程为：先将上板和下板用螺钉连接，然后插入铰链销子，最后安装挡圈。上板和下板之间的定位采用定位面、定位槽和定位孔/销。图2和图3为上板和下板的尺寸与公差标注初步方案。

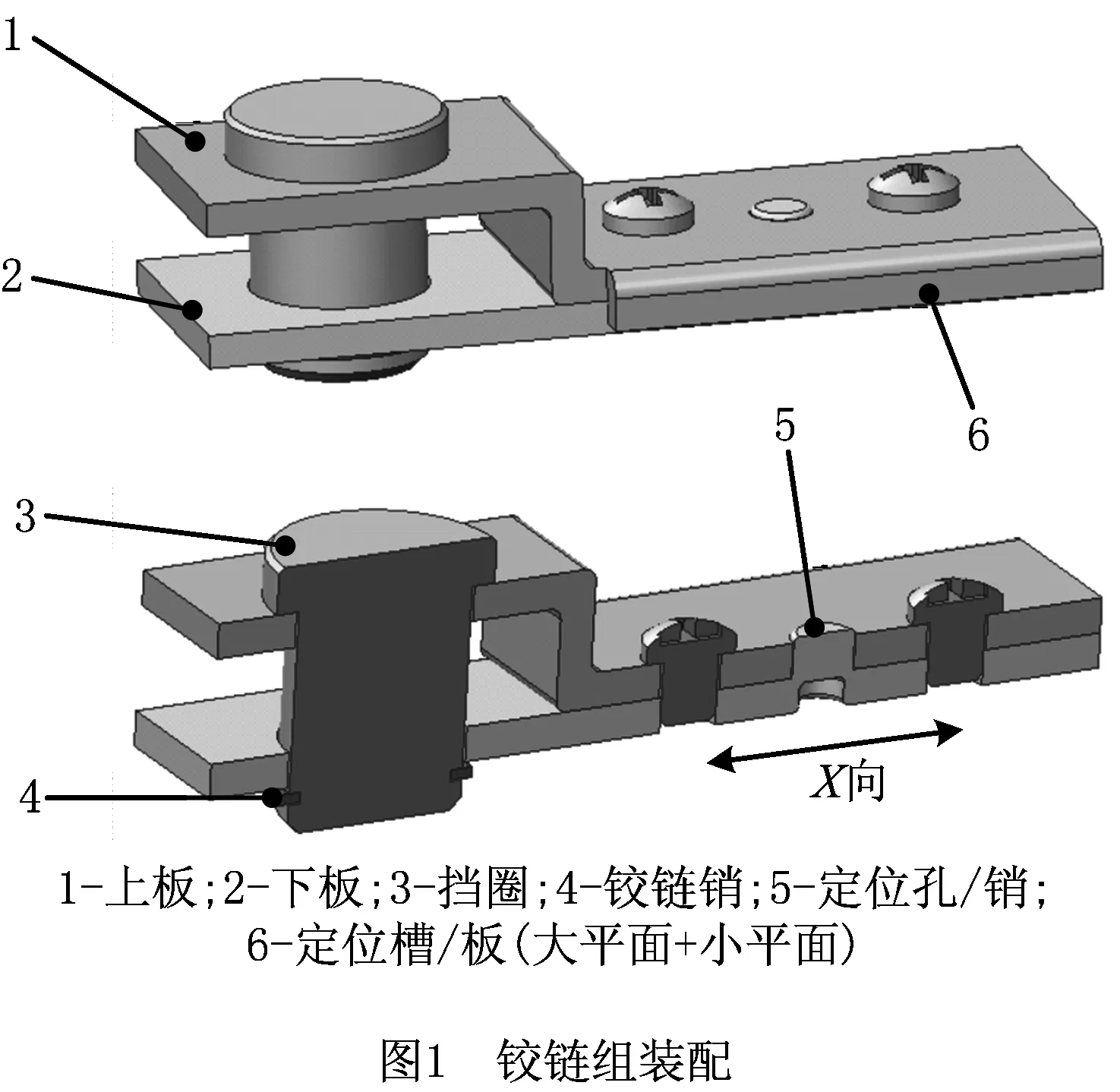
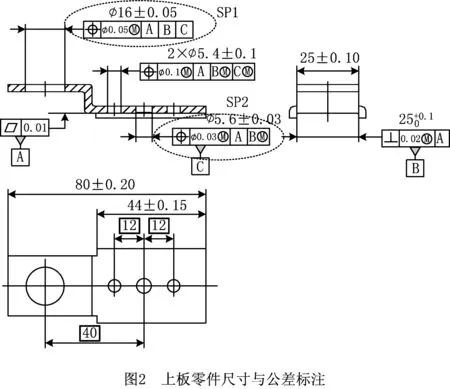
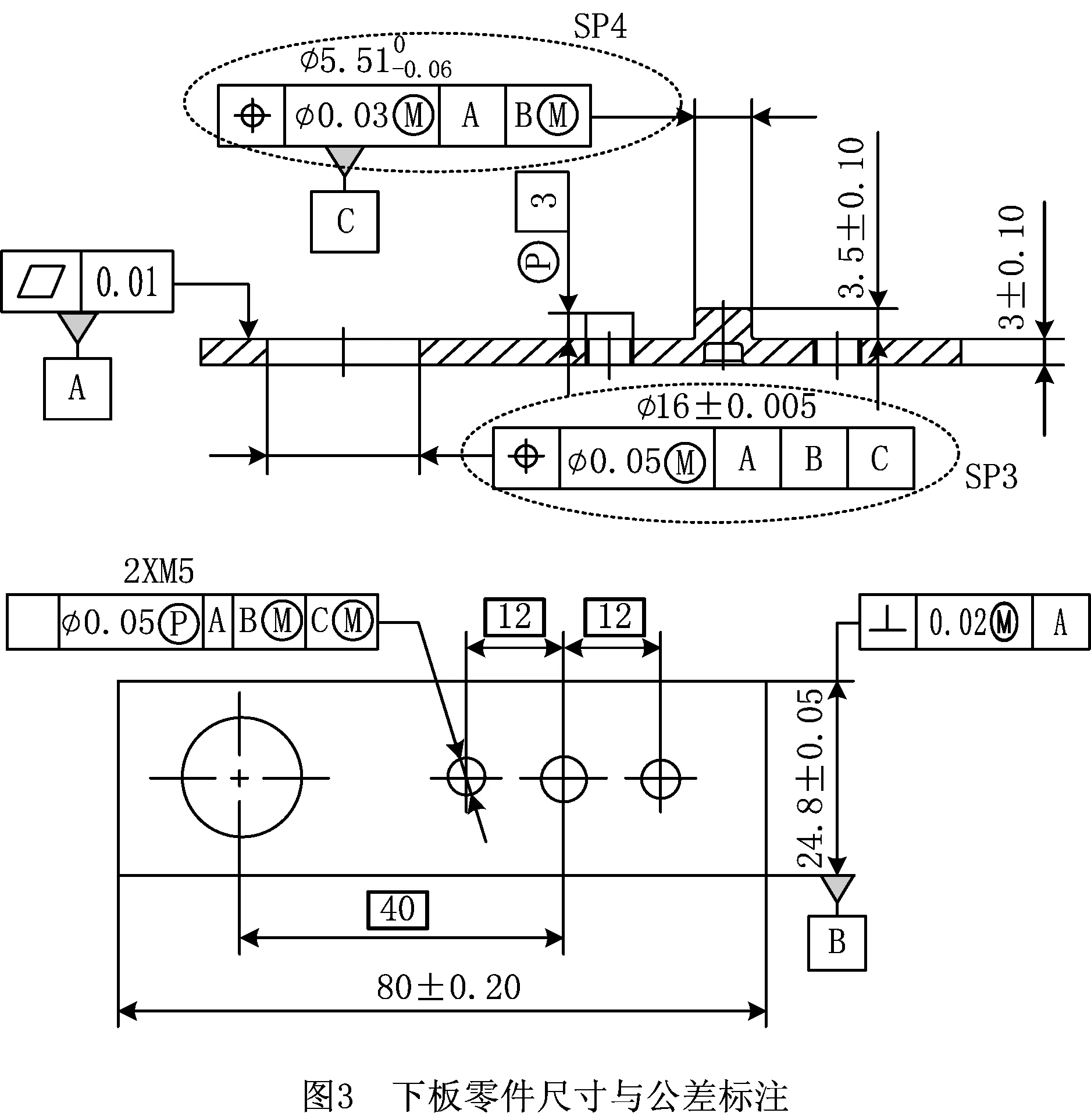
上板和下板中铰链孔的公差标注SP1/SP3均采用位置度公差控制、公差值相同，由于与铰链销装配为间隙装配，为保证间隙装配，对被测要素采用最大实体要求。SP1/SP3几何规范要求无论该实际铰链孔的尺寸和位置如何变动，应始终确保一空间不得被侵犯，该空间即是孔的最大实体实效边界。最大实体实效边界具备2个特点：①该边界以内没有任何材料；②该边界与基准的方向和位置关系理想，如图4所示。

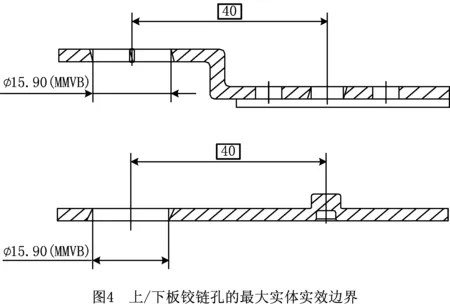
最大实体实效边界的尺寸用下式计算：

DMMVB=DMMC-t位置度

=φ15.95-0.05=φ15.90。

(1)

式中：DMMVB为铰链孔的MMVB尺寸，DMMC为铰链孔的最大实体尺寸，t位置度为位置度公差。

2.2 公差补偿

对于几何规范SP1/SP3，当且仅当被测要素(被测孔)处于最大实体状态(Maximum Material Condition, MMC)时，被测要素的导出要素(轴线)允许的最大位置度误差为φ0.05；同时，被测孔的实际直径须处于最大实体尺寸MMS(φ15.95)和最小实体尺寸LMS(φ16.05)之间。而当被测孔远离最大实体状态时，有额外的公差补偿(Bonus Tolerance)产生。位置度公差补偿可由下式计算出：

tbonus=Da-DMMC。

(2)

式中：Da为孔的实际尺寸，DMMC为孔的最大实体尺寸。则允许的最大位置度误差为

t位置度/允许=t位置度+tbonus。

(3)

式中t位置度为几何公差框格中的位置度公差值。

图5为几何规范SP1的动态公差示图，从中可看出，随着被测孔的实际尺寸变大，允许的位置度公差也随之变大，从而使零件的合格率提高。

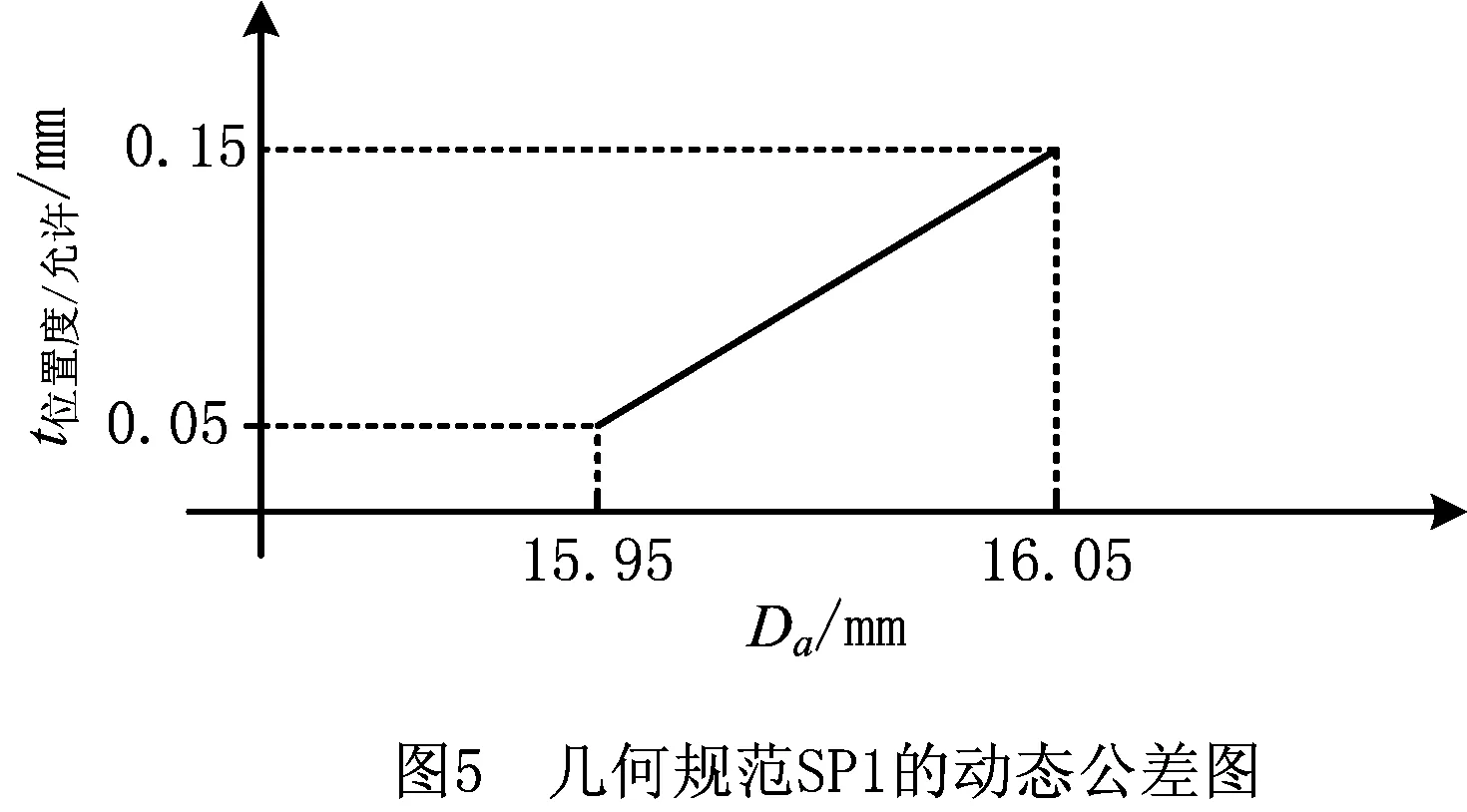
2.3 可装配性设计

设计铰链销的尺寸时，要求铰链销的体外作用尺寸小于等于φ15.90才能保证其100%顺利穿过上/下板的铰链孔。因此，铰链销的直径可标注成图6所示，并采用包容要求，此时销轴的体外作用尺寸不超出φ15.90，满足装配要求。

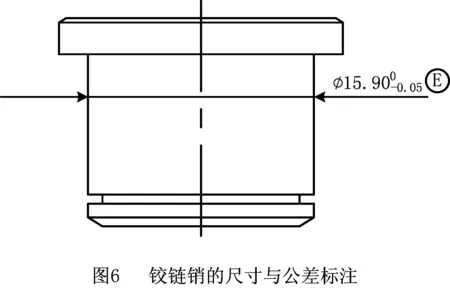
上/下板铰链孔的最大实体实效边界以内可认为是相对基准系的理想位置而存在的一个空间，要使铰链销能够同时装入上/下板铰链孔中，须要求上/下板铰链孔的最大实体实效边界同轴。此时，理应要求上/下板的定位槽/板或定位孔/销之间采用“紧配合”来保证上/下板最大实体实效边界同轴。但是，为了提高在流水线上的装配成功率，一般在定位槽/板之间或定位孔/销之间留有装配间隙，以允许由此间隙来调整上/下板之间相对位置来保证铰链孔最大实体实效边界对齐。在考虑“允许利用定位特征之间的间隙来调整相配件之间的方向或位置”的情形下，图2和图3的几何公差规范方案需进行调整。

3 最大实体要求应用于基准要素与基准偏移

3.1 最大实体要求应用于基准要素实例分析

在图1例中，若上板定位孔与下板定位销远离最大实体实效状态时，它们之间装配存在间隙，即上板可在下板上左右移动、晃动。为了放松铰链孔的公差要求，应允许“当上/下板铰链孔的最大实体实效边界和定位孔C之间的距离偏离理论正确尺寸40时，利用定位孔/销之间存有的配合间隙，沿X向调整上/下板的相对位置来使得铰链销(图6)装配成功”，即应对SP1/SP3的基准要素C采用最大实体要求。这种因基准要素(定位特征)之间为间隙配合，允许被测要素的方向或位置有一定偏差的定义称之为基准偏移(Datum Shift，DS)[20]。基准偏移同样适用于SP1/SP3几何规范中的基准B(定位槽/板)。因此，图2和图3中的SP1/SP3几何规范更改为图7所示。

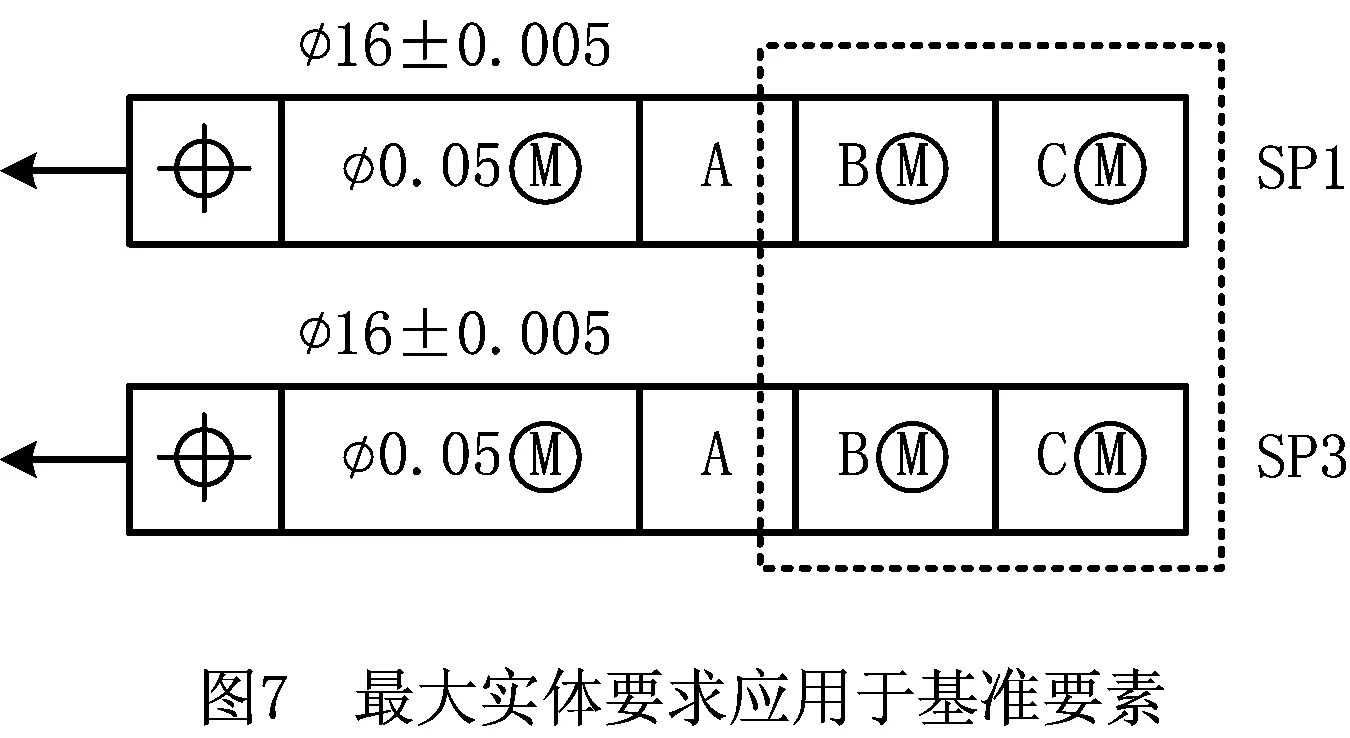
图2和图3对定位孔/定位销C的几何规范SP2/SP4中的被测要素采用了最大实体要求，要求定位孔/定位销C的体内存在一个最大实体实效边界(Datum Maximum Material Virtual Boundary, DMMVB)，边界尺寸分别为

(4)

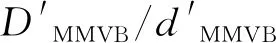
以上板为例，根据ISO5459:2016[21]，被测要素的最大实体实效边界和基准要素的最大实体实效边界若满足以下2个条件：①被测要素的最大实体实效边界和基准要素的最大实体实效边界之间保持理想的位置关系(理论正确距离为40)；②被测要素最大实体实效边界空间和基准要素最大实体实效边界空间同时不受侵犯，则被测要素的位置度公差要求合格，如图8所示。

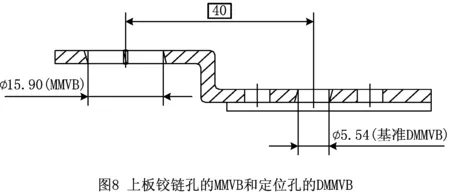
3.2 检具设计

综合量规是边界的现实“代表”，验证最大实体实效边界和DMMVB能否满足上述2个条件的最常用方法采用检具(综合量规)检测。图9为一种检测上板的检具设计方案示图，其中检测销的基本尺寸为φ15.90(反映被测要素最大实体实效边界占用的空间)，检具定位销的直径为φ5.54(反映基准要素C的DMMVB占用空间)，检测销和检具定位销之间的距离为理论正确尺寸40。检测销、检具定位销及它们之间的距离40均应在检具精度范围内。检测流程为：先将上板零件1置于检具体3上，由其定位面(基准A)、定位板(中心平面为基准B)、定位孔(基准C)定位，再用检测销2穿过被测铰链孔4。在检测过程中，若上板零件的定位孔5和检具上的定位销6之间存有间隙，允许上板零件在检具上晃动来调整相对位置来使得检测销穿过被检测孔；若检测销2能顺利通过上板铰链孔4，SP1位置度合格。从图9可以看出，若上板定位孔的体外作用尺寸增大，配合间隙也增大，上板在检具上调整的空间越大，允许上板铰链孔的轴线在X向的距离偏差也就越大。

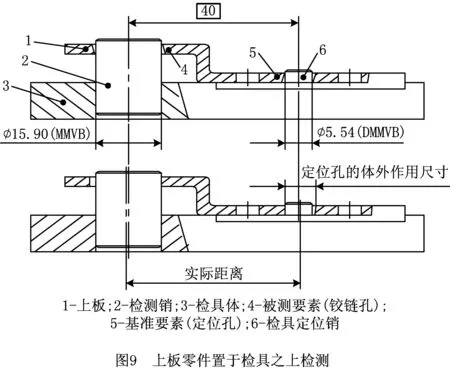
3.3 基准偏移

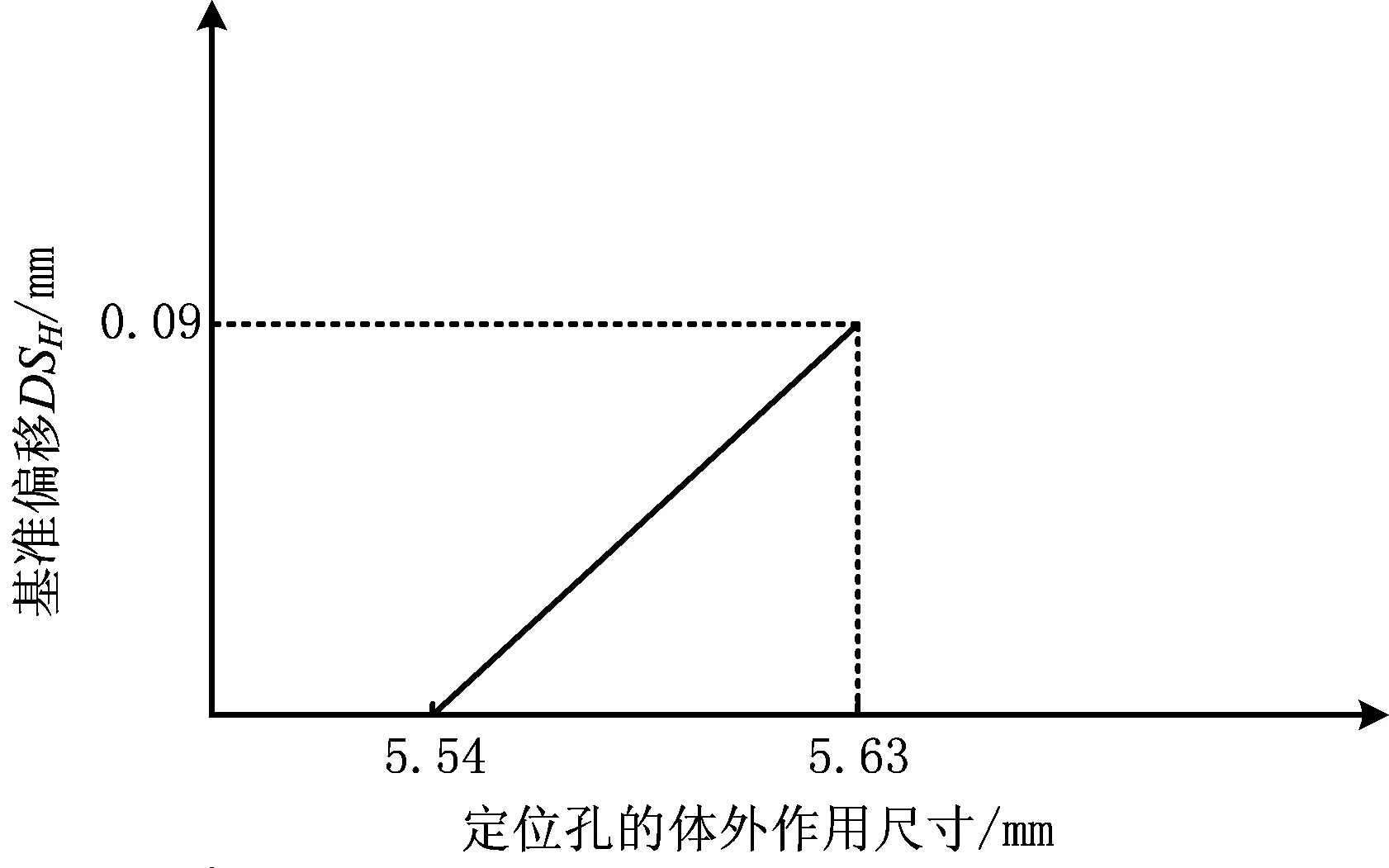
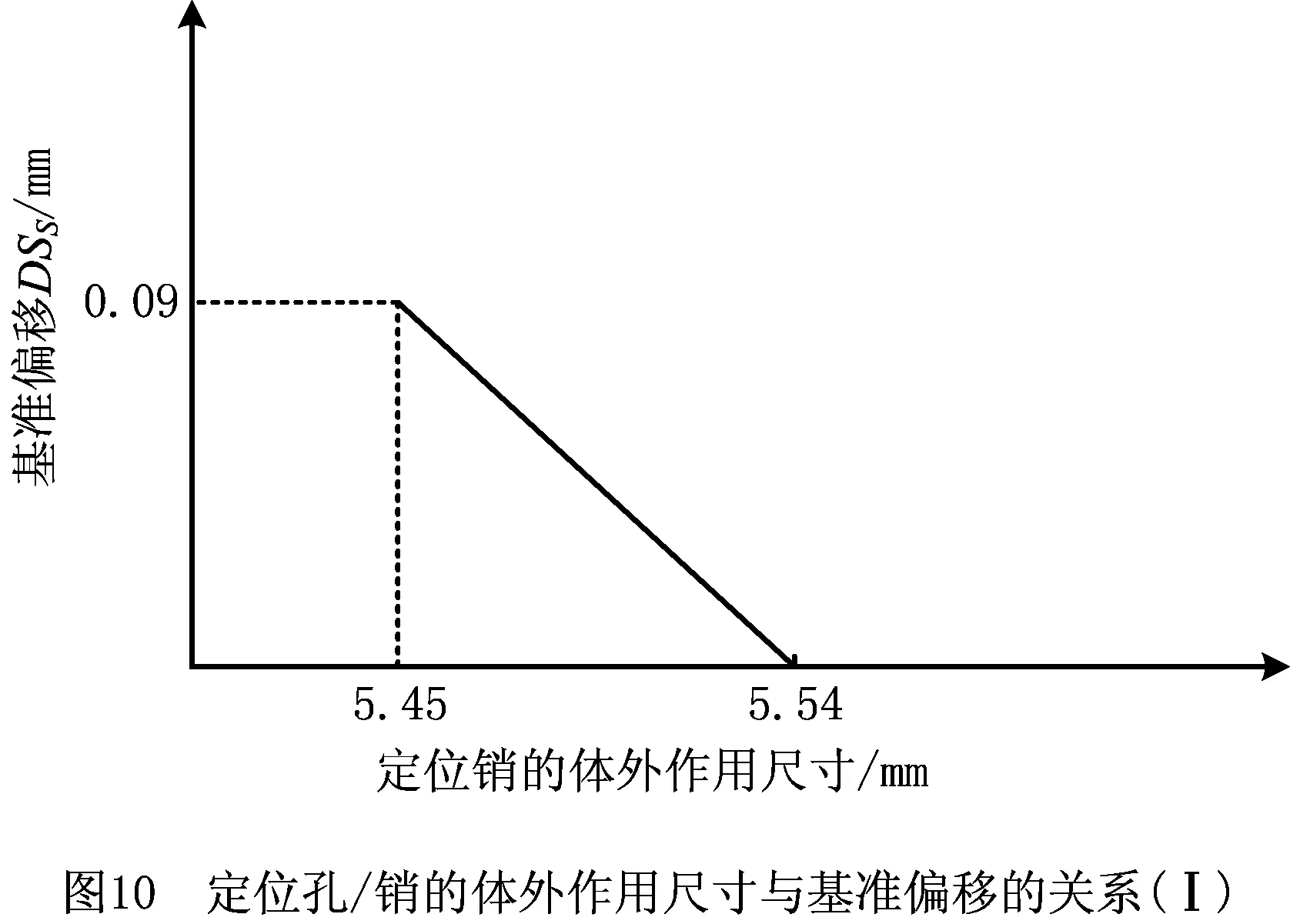
基准偏移是零件基准要素与检具模拟基准之间允许的松动(偏移)，基准偏移放松了被测要素的公差要求。事实上，允许被测要素在X向的超差(X向的基准偏移)和基准要素的体外作用尺寸存在如图10所示的关系。当基准要素的体外作用尺寸远离其DMMVB时，被测要素的几何公差可以获得来自基准要素(定位孔/销)的补偿DSH/DSS：

(5)

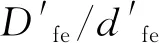
4 基准要素不能应用MMR的情况

4.1 基准要素不能应用MMR实例分析

焊接是汽车白车身制造中最常见的一种装配工艺，图11为某汽车钣金件焊装现场图，先将其在工装上采用“一面两销”定位，然后焊接(激光焊或点焊)，同时要求保证焊后相关过孔同轴。尽管所采用的定位孔/销之间存在装配间隙，但装配连接工艺并不允许利用定位特征之间的间隙来调整相配件之间的方位关系，需要讨论此种情形下能否对基准要素(定位孔)应用MMR。

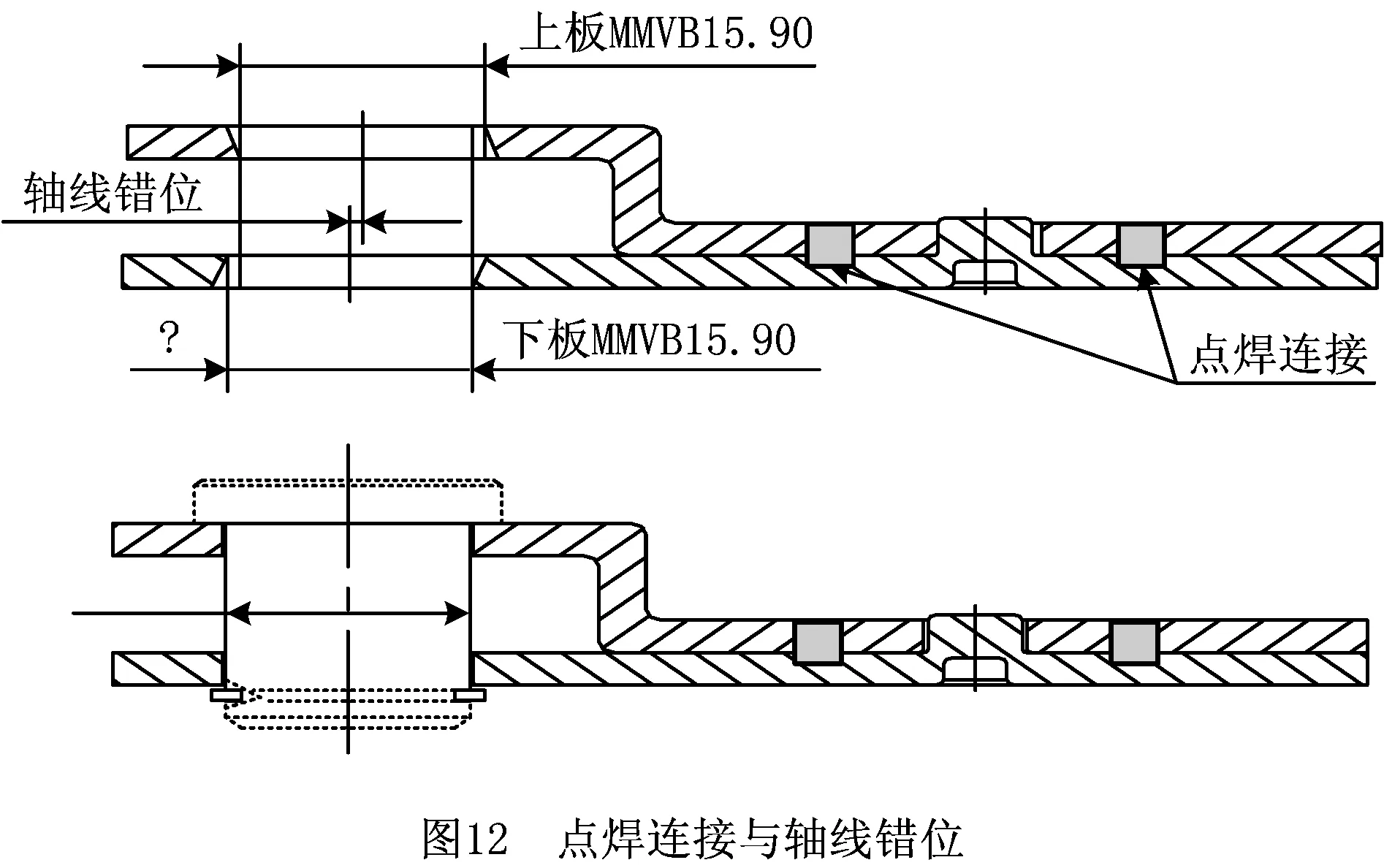
为研究方便，仍以图1所示铰链组件装配为例进行分析，其装配工艺变更为：上板和下板之间仍用A/B/C基准定位，用定位孔/销对上/下板进行定位后即行点焊，最后插入铰链销。点焊连接的定位孔/销在装配后必然存在间隙，导致上板或下板的铰链孔相对于理想中心出现随机的轴线错位，如图12所示。

4.2 装配实效边界的提出

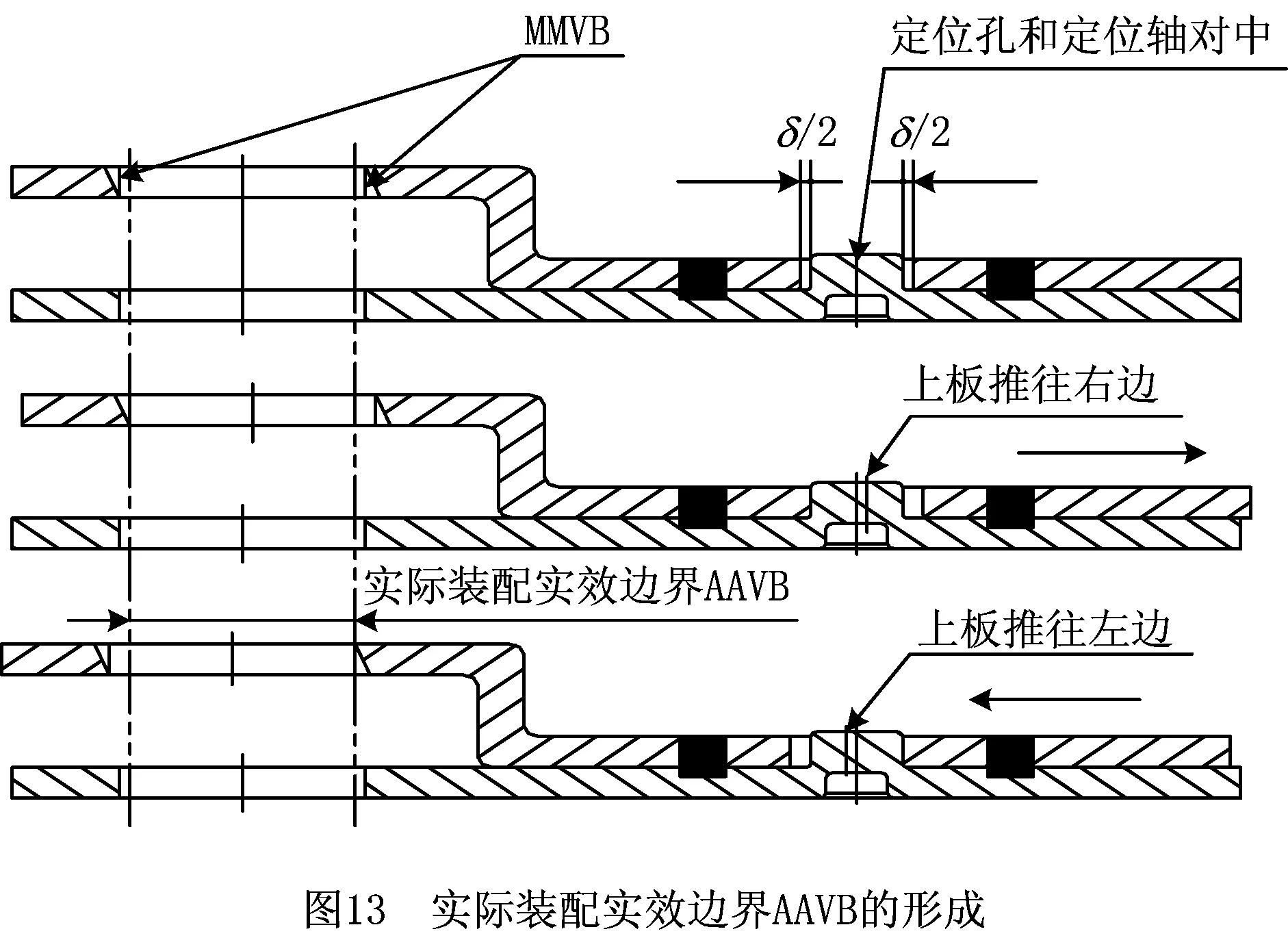
如图13所示，由于定位孔/销之间配合间隙δ的存在，上板铰链孔的MMVB随机左/右移动(假定下板不动)，最终形成了一不被侵犯的无材料公共空间，将该空间的边界定义为实际装配实效边界(Actual Assemble Virtual Boundary，AAVB)。定位孔/销的配合间隙δ本身也在一定范围内随机变动，δ越大、AAVB越小。实际装配实效边界实际装配实效边界尺寸的计算式为：

DAAVB=Dfe-δ。

(6)

式中：Dfe为铰链孔的体外作用尺寸，δ为定位孔/销之间的配合间隙。

考虑可能对装配最不利的极限情况，上板出现在左/右极限位置(假定下板不动)，则始终存在一个固定不变的空间不被侵犯，如同最大实体实效边界形成的原理一样，铰链孔的最大实体实效边界随机平移最终形成一个永远无材料的最小公共空间，该最小公共空间的边界定义为最小装配实效边界(Minimum Assemble Virtual Boundary，MAVB)。

根据式(6)，当δ最大、且Dfe处于最小时，实际装配实效边界等于最小装配实效边界，最小装配实效边界分析计算如下：

(1)如图14所示，上/下板定位孔/定位销之间的配合间隙δ为：

(7)

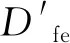
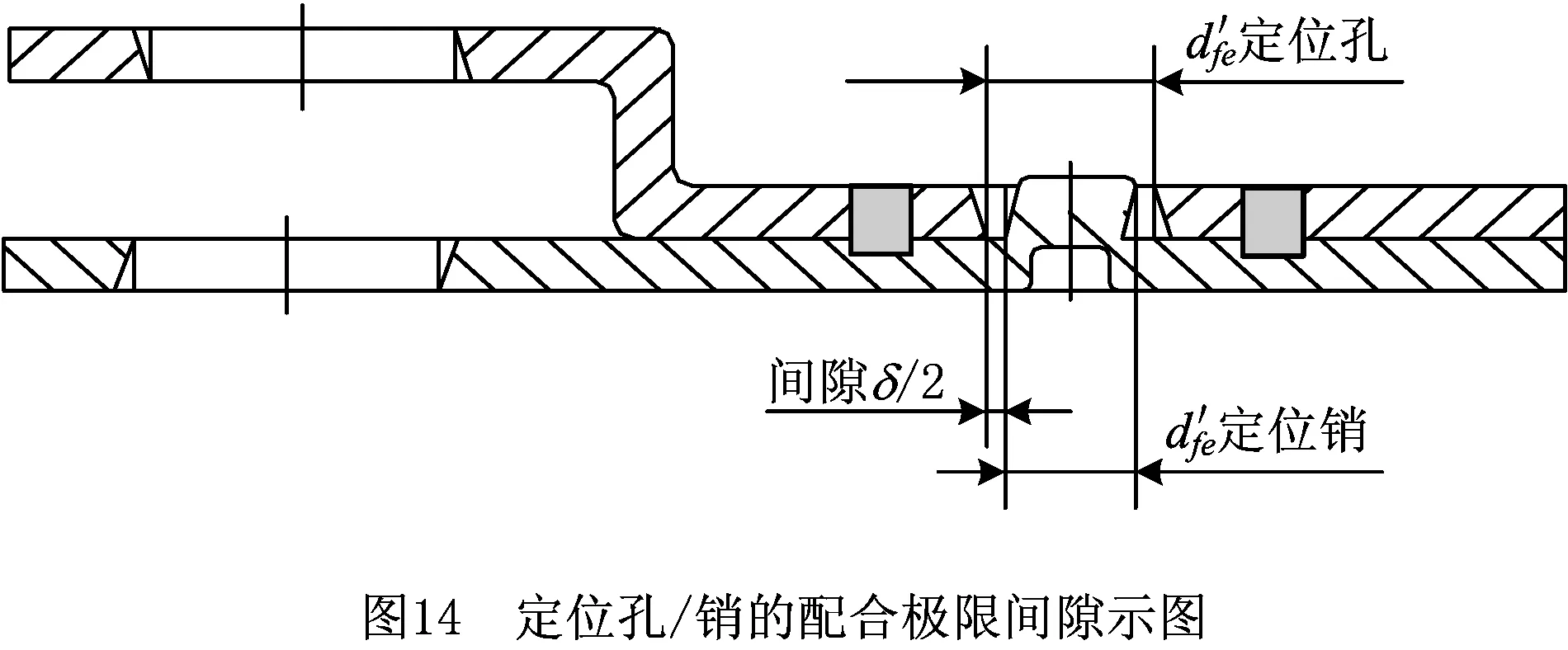
而定位孔/销的体外作用尺寸的计算式为

(8)

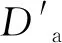
由式(7)和式(8)可知，对于一批产品而言，满足以下条件：

(9)

则δ最大，最大值为

=φ5.63-φ5.45=0.19。

(10)

(2)铰链孔的体外作用尺寸Dfe的最小允许值为DMMVB；

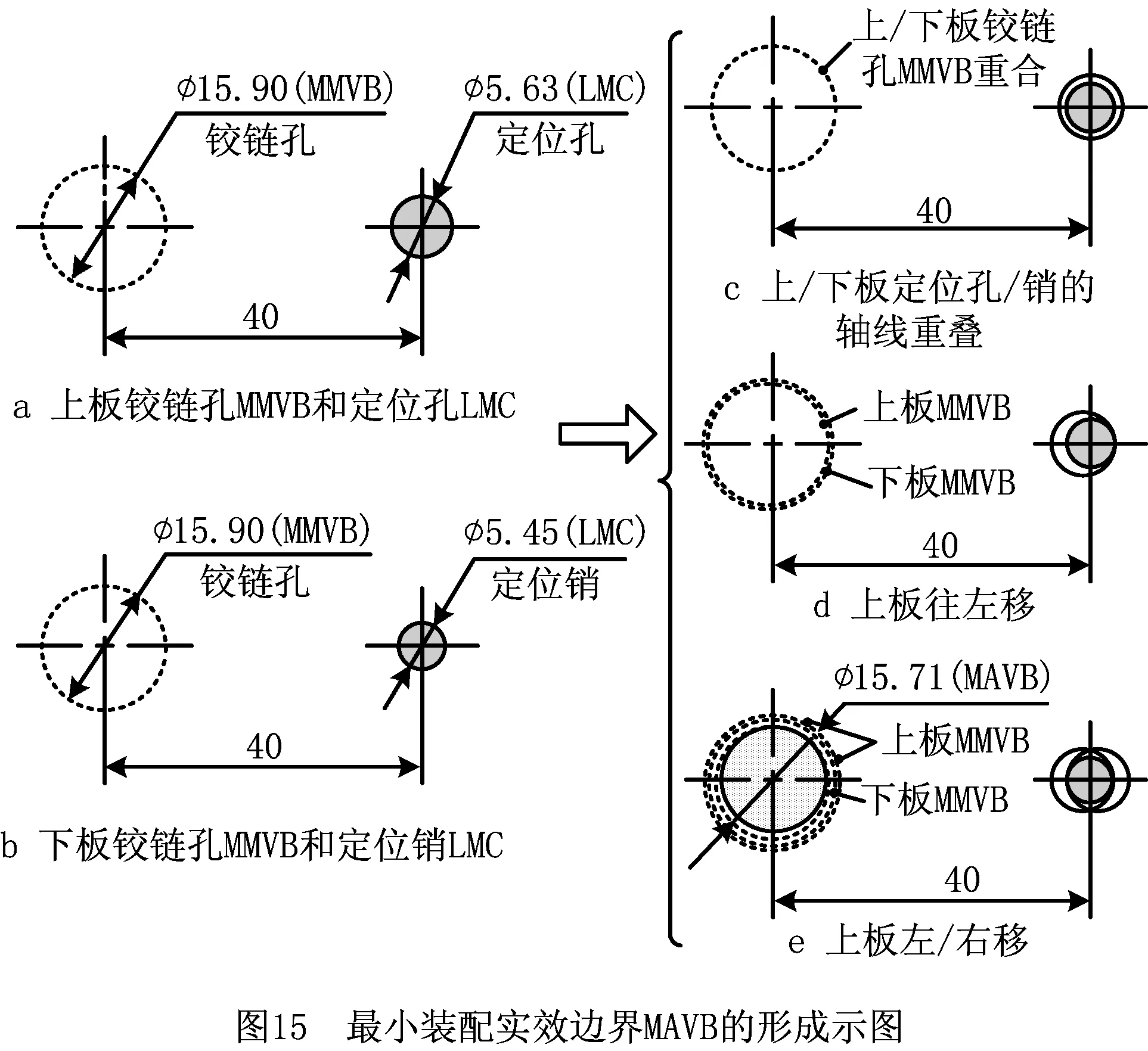
(3)最小装配实效边界MAVB的形成如图15所示，其尺寸为

DMAVB=DMMVB-δmax

=φ15.90-0.19=φ15.71。

(11)

式中：DMMVB为两个铰链孔的最大实体实效尺寸，δmax为上板定位孔和下板定位销之间的最大配合间隙。

4.3 可装配性设计

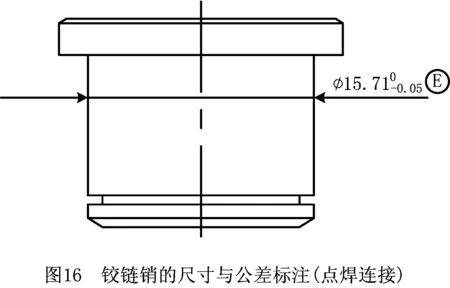
若要使铰链销穿过上/下铰链孔，保证装配互换，铰链销的体外作用尺寸不得超出上/下板铰链孔的最小装配实效边界，即铰链销的体外作用尺寸不超出φ15.71，才能保证100%不发生装配干涉。铰链销尺寸及公差更改标注如图16所示。

5 LMR应用于基准要素与基准偏移

5.1 SP1/SP3的优化标注

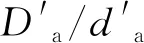
如图17和图18所示，其中SP1/SP3标注对被测要素采用最大实体要求，对基准要素B/C则采用最小实体要求，属MMR和LMR混合标注情形。有3点需要说明：①因SP1/SP3中定位孔/销(基准C)的作用是装配定位，起作用的边界是孔的最大内切圆柱/轴的最小外接圆柱，根据ISO5459:2016[21]，SP1中的C基准附加[X]符号，表示拟合算法采用

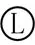
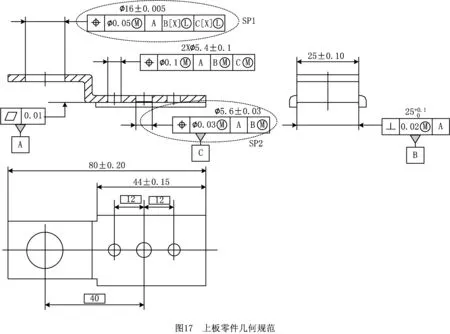
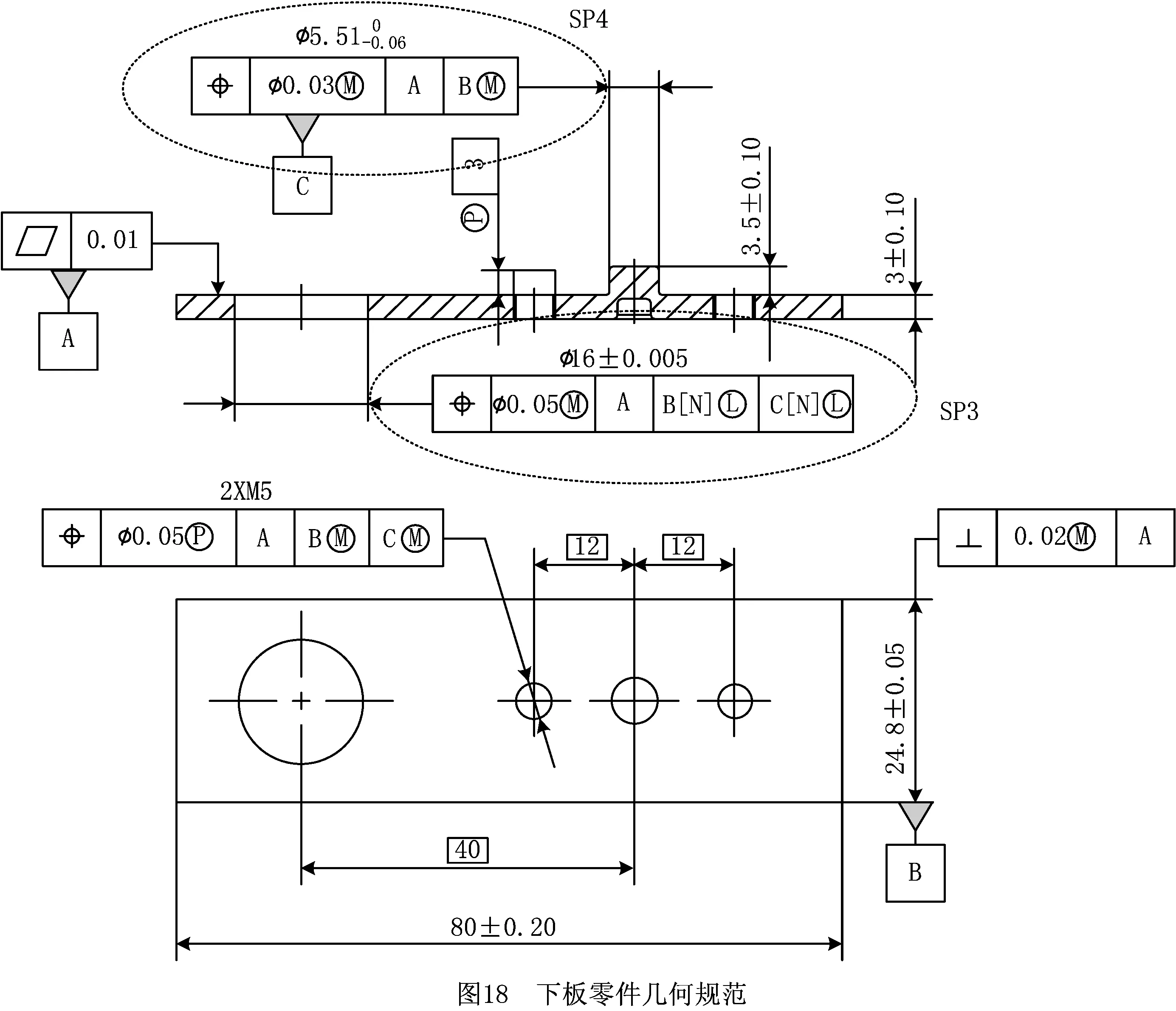
5.2 优化后的检具检测方案

由于对基准要素采用最小实体要求，最小实体要求与最大实体要求的性质不同，最小实体要求的临界边界是从最小实体状态向体内方向叠加而形成，这与综合量规的检验原理不一致。原理上设计不出能够随内特征尺寸减小或体外要素尺寸增大、允许位置度误差增大的综合量规。但图17和图18采用的是体外约束的最小实体要求，它是一种特殊的要求，虽然SP1/SP3基准要素的LMVB在材料内部，但仍可采用检具检测。

以检测上板SP1为例，其检具设计方案如图19所示，检具操作方法和常规检具操作方法有所区别：首先将零件置于检具基座上，使检具上A基准定位面5和零件的A面紧贴，检具上的B基准定位板6插入零件B基准槽，检具上的C基准定位销4插入零件C基准孔；通常情况下，检具的定位特征和零件的定位特征之间存有间隙(零件在检具上可活动)，此时需将零件推向任意极限位置，然后保持零件不动、插入检测销，若检测销1的工作部分能够顺利通过被测孔，则SP1位置度合格。将零件推向任意极限位置模拟了零件在装配时(点焊之前)可能出现的极限位置，若在极限位置检测销1的工作部分能通过，则在非极限位置检测销1的工作部分也能通过，SP1位置度合格。

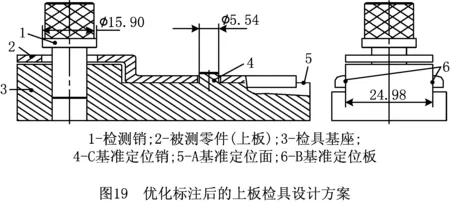
5.3 基准偏移补偿量

图17和图18中的SP1/SP3对基准要素C采用最小实体要求，当基准要素C体外作用尺寸远离LMC时，被测要素的几何公差可以得到来自基准要素定位孔/轴的偏移补偿DSH/DSS：

(12)

式中：DSH表示上板定位孔的基准偏移，DSS为下板定位轴的基准偏移。

基准偏移与基准要素的体外作用尺寸呈现关系如图20所示。以上板零件标注(图17)为例，铰链孔的SP1位置度可从基准C得到偏移补偿量为：

(13)

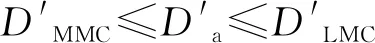
5.4 上板铰链孔允许的位置度公差及其合格判据

上板铰链孔SP1位置度公差对被测要素采用MMR、对基准要素C采用LMR(只讨论基准C的基准偏移)。当铰链孔的实际状态处于MMC时，允许的位置度为：

=φ0.05+DSH。

(14)

而当铰链孔的实际尺寸远离最大实体状态MMC时，实际允许的位置度有额外的公差补偿产生

tBonus=Da-DMMC。

(15)

该额外的位置度公差补偿可叠加入式(14)中：

t位置度/允许=t位置度+tBonus+DSH

=t位置度+(Da-DMMC)+DSH

=φ0.05+(Da-DMMC)+DSH。

(16)

根据式(16)，若铰链孔SP1位置度合格，须满足以下不等式：

f位置度≤t位置度/允许=φ0.05+

(Da-DMMC)+DSH。

(17)

式(15)～式(17)中：Da为铰链孔的实际尺寸，f位置度为铰链孔的实际位置度误差。

SP1铰链孔的体外作用尺寸计算式为：

Dfe=Da-f位置度。

(18)

当Da=DMMC、且f位置度=t位置度/允许时，铰链孔合格、Dfe最小，最小值为：

Dfe/min=DMMC-t位置度/允许

=DMMC-[t位置度+(DMMC-DMMC)+DSH]

=DMMC-t位置度-DSH

=DMMVB-DSH。

(19)

因此，铰链孔SP1合格判据为：

(20)

5.5 验证装配实效边界

图17和图18中的SP1/SP3几何规范对基准要素C采用最小实体要求，与上一节采用独立原则相比，其实际装配实效边界AAVB的计算发生了变化。

根据式(6)，实际装配实效边界的尺寸为：

DAAVB=Dfe-δ

(21)

将不等式(17)代入式(21)，则有：

DAAVB≥Da-[φ0.05+(Da-DMMC)+

(22)

整理得：

(23)

又因DMMVB=DMMC-φ0.05，代入式(23)：

(24)

再整理：

(25)

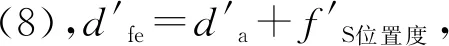
(26)

结合不等式(25)和式(26)，有

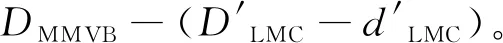
(27)

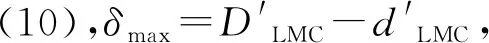
DAAVB≥DMMVB-δmax。

(28)

由式(11)，DMAVB=DMMVB-δmax，得出：

DAAVB≥DMMVB。

(29)

式(29)表明，当对SP1/SP3中的基准要素C采用最小实体要求时，上/下板装配形成的装配实效边界不小于最小装配实效边界(MAVB)，即按图16制造的铰链销也能100%顺利装配，不会发生干涉。但因为基准偏移DS的存在，放松了对铰链孔的位置度公差要求，增加了零件的合格率，从而实现了设计优化。

6 结束语

在几何公差设计时，对被测要素采用最大实体要求可使被测要素的几何公差可从尺寸公差获得补偿；对基准要素使用最大实体要求可使被测要素的几何公差带从基准要素获得基准偏移补偿。而当实际装配过程中无法利用定位特征的配合间隙来调整相配件之间的位置或方向时，为防止或减弱因零件错位而导致的装配干涉，不应对几何规范中的基准要素采用最大实体要求。

本文提出了装配实效边界和最小装配实效边界的概念，研究了实际装配实效边界的形成，指出为了保证装配互换性，零件的几何特征(或几何要素)因装配而形成的最小装配实效边界在任何工况下均不得被超出。若因为装配工艺的原因导致零件之间的方向和位置无法在装配过程中进行调整，对基准要素采用独立原则不是最优设计，设计人员可在权衡零件合格率和检验成本之后，再选择对基准要素采用独立原则或体外约束的最小实体要求。

铰链组装配实例中的研究对象为非成组要素，而成组要素的最大实体要求/最小实体要求混合应用与标注需进一步分析和研究。