带批和离散机柔性流水车间问题的混合异步次梯度优化的拉格朗日松弛算法
2020-05-08王薛苑
轩 华,王薛苑,李 冰
(郑州大学 管理工程学院,河南 郑州 450001)
0 引言
钢铁业的一体化生产和化工业的许多实际生产问题都可归结为柔性流水车间问题(Flexible Flow Shop Problem, FFSP)[1]。例如,炼钢—连铸—热轧一体化生产过程由3个阶段组成,经炼钢阶段加工完成的钢水在连铸阶段组成不同的浇次进行浇铸,同一浇次的多炉钢水要在同一连铸机使用相同结晶器连续不断地进行加工,最后在热轧阶段将连铸板坯轧制成带钢。在该过程中,每个阶段有多台并行机,每个工件依次经过这3个阶段进行加工,因此,该结构可看作是FFS。不同于一般FFS的是,该生产过程中,连铸机为串行批处理机,即它要求一个浇次(批)内的炉次(工件)连续不间断地进行加工,一批的加工时间为该批内所有工件的加工时间之和;而其他阶段的机器为离散机,即一台机器一次至多加工一个工件。因此,本文研究一类带批和离散机的FFSP,其中,批处理机可以在任何一个加工阶段。
批处理分为并行批处理和串行批处理两类。前者的批加工时间是该批内工件的最大加工时间,而后者的批加工时间则是组成该批的所有工件的加工时间之和。近年来,这两类批处理的调度问题已经受到了广泛的关注。
针对含并行批处理机的情况,文献[2]提出了差分进化算法求解阶段1为多台并行批处理机,而阶段2含多台离散机的两阶段FFSP,目标是最小化makespan;文献[3]对阶段1有3台等同的并行批处理机而阶段2有一台离散机的两阶段FFSP,提出了遗传算法以最小化makespan;文献[4]则研究了每阶段有并行批处理机的两阶段FFSP,考虑了交货期和工件准备时间,目标是总加权拖期,提出了结合邻域搜索法的迭代阶段分解方法。文献[5]将钢化玻璃制造的切割—磨边—回火过程提炼为前两个阶段有多台非等同机而第三个阶段有1台并行批处理机的三阶段FFS,为最小化makespan,提出了构造启发式、遗传算法,模拟退火算法求解实际大规模问题。文献[6]针对某一阶段含多台并行批处理机的多阶段FFSP设计了一种基于时间窗的蚁群算法,目标是最小化makespan。
针对串行批处理调度问题,文献[7]将炼钢—连铸—热轧一体化生产环境归结为作业车间结构,其中连铸机为串行批处理机,提出了基于工件分解和次梯度法的LR算法以最小化提前/拖期惩罚、连轧断开损失惩罚和板坯等待时间惩罚之和,通过测试8个炉次的一组实例验证了算法的有效性;文献[8-10]针对炼钢—连铸的作业车间问题分别提出了多Agent蚁群算法、改进NSGA-Ⅱ算法和两阶段优化算法,其中文献[8]是最小化炉次的流程时间,文献[9]旨在最大化炉次匹配度、最小化炉次等待时间及最小化浇次开浇提前/拖期时间,文献[10]的目标是保证浇次准时开浇、浇次内炉次连浇和等待时间最小。文献[11]将炼钢—连铸生产抽象为流水车间问题,提出了离散粒子群算法以最小化总完工时间。文献[12]提出了一种混合模糊粒子群算法求解炼钢—连铸的FFSP,目标是最小化makespan和炉次在工序间的等待时间;文献[13]为最小化平均滞留时间、未启动的浇次开工的提前/拖期、断浇、初始调度和新调度中工序开始时间之差的总和、初始调度和新调度中不同机器上加工的工序数的加权和,提出了改进人工蜂群算法进行求解炼钢—精炼—连铸生产的多阶段FFS的再调度问题;文献[14]为某阶段为串行批处理机的多阶段FFSP设计了基于批分解的改进LR算法以最小化总加权完成时间,为解决同一问题,文献[15]则提出了改进遗传算法;利用上述基于批分解的改进LR算法,文献[16]求解了从炼钢—连铸—热轧生产提炼出的中间阶段为批处理机的双目标问题(即最小化总加权完成时间和滞留时间之和)。
然而,上述研究很少考虑工件的动态到达,大多研究的是静态调度,并且关于总加权完成时间问题的探讨很少,求解方法多为基于人工智能的近似算法,既有研究(文献[14])虽求解了多达60个工件的中小规模问题,但当求解规模增大时,每次迭代求解松弛问题消耗的运行时间较长,尤其是批数较多的大规模问题。本文旨在利用基于最优化的近似方法提出一种算法以有效求解这类含批处理机和离散机的动态FFS总加权完成时间问题,因此,提出了混合异步次梯度优化的拉格朗日松弛(Lagrangian Relaxation mixed with Interleaved Subgraident Optimization, LR&ISO)算法,设计了异步次梯度优化使得每次迭代仅最优求解一个批级子问题,以加速LR的求解过程和改善解的质量。本文扩展了文献[14]所提出的LR算法理论,解决了其求解大规模问题效率较低的问题。
1 数学模型
1.1 问题设置
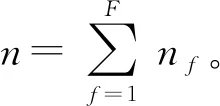
1.2 IP模型
(1)集合
j表示工件集,j=1,…,n;
s表示阶段集,s=1,…,S;
f表示批集,f=1,…,F;
k表示时间集,k=1,…,K。
(2)参数
Ms表示阶段s的并行机数;
Pjs表示工件j在阶段s的加工时间;
wj表示工件j的权重;
Rj表示工件j的动态到达时间;
hfq表示批f内的第q个工件,q=1,…,nf;
Ts,s+1表示阶段s到阶段s+1的传送时间;
STjs表示工件j在阶段s的调整时间,令l为批处理机所处阶段,则当s=l且j=hf1时,其值大于0,否则都为0。
(3)决策变量
yjsk表示若时刻k工件j正占用阶段s的机器,则其值为1,否则为0;
cjs表示工件j在阶段s的完工时间;
bjs表示工件j在阶段s的开工时间。
基于文献[14],建立整数规划(IP)模型:
(1)
(2)
bj1≥Rj,j=1,…,n;
(3)
bjs≥bj,s-1+Pj,s-1+Ts-1,s,j=1,…,n,
s=2,…,S;
(4)
bhfq,l+Phfq,l=bhf,q+1,l,f=1,…,F,
q=1,…,nf;
(5)
bjs-STjs≤k+K(1-yjsk),j=1,…,n,
s=1,…,S,k=1,…,K;
(6)
cjs=bjs+Pjs-1,j=1,…,n,s=1,…,S;
(7)
yjsk{0,1},j=1,…,n,s=1,…,S,
k=1,…,K。
(8)
其中:目标(1)旨在最小化所有工件的TWC值;约束(2)说明了在任一阶段任一时刻正在加工的工件总数不能超过该时刻可利用的机器数;约束(3)确保了每个工件在其到达生产系统之前不能开始在第一阶段的加工;约束(4)表示了一个工件的相邻两工序之间的加工优先级关系;约束(5)表示了在批处理阶段,同一批内,前一个工件加工完成后下一工件立刻开始加工,保证了同一批内工件加工的连续性;约束(6)说明了工件占用机器的时间约束;约束(7)表示了同一工件开工时间和完工时间的关系;约束(8)说明了决策变量yjsk是0-1变量。
上述模型虽然与文献[7]相似,但两者有不同之处,体现在:①本文研究的是一般的含批处理机和离散机的多阶段FFSP,因此考虑了这类问题的关键约束,忽略了在特定生产环境下的某些具体技术要求,而文献[7]考虑到连铸—热轧间不同的衔接方式,具体研究了炼钢—连铸—热轧的作业车间问题;②考虑到串行批处理机要求同一批内的工件按照一定的顺序连续地在该阶段的一台机器上进行加工,因此,将其表示为约束的形式,而文献[7]则通过目标函数的一个惩罚项来体现该要求;③考虑到工件到达的动态特性,本文引入了工件释放时间约束,而文献[7]假定所有工件都在时刻1到达生产系统;④本文模型旨在降低生产费用和在制品库存及提高准时传送,而文献[7]针对钢铁企业的一体化生产过程考虑了更多因素。
2 LR&ISO算法
传统的LR算法要求松弛耦合工件的约束从而将松弛问题分解为每个针对一个工件的工件级子问题[7]。1.2节中约束(2)和约束(5)均关联了不同工件,因此,若使用传统LR算法则需松弛这两组约束,而松弛的约束越多,收敛性越差,下界更松[14],故而根据模型的批处理生产特点,本文基于批分解方式改进LR。
2.1 拉格朗日松弛
引入非负拉格朗日乘子{γsk}将约束(2)松弛到目标函数中,构成拉格朗日松弛问题:
s.t.
(3)~(8);
γsk≥0,s=1,…,S,k=1,…,K。
(9)
拉格朗日代理对偶问题定义为
s.t.
(3)~(9)。
上述LR问题的第二项与决策变量无关,因此计算时先将其忽略,而第一项是对所有工件求和,即对所有批求和,因此,可进一步将第一项表示为所有批内工序之和,即
给定γ,可将LR问题分解为F个批级子问题:
s.t.
(3)~(8)。
由此,可将LR问题重新表述为
s.t.
(3)~(9)。
2.2 子问题的异步求解
待求解的批级子问题由nf个工件的多个工序构成,每个工序可能有多个紧前工序或紧后工序,故单一方向时间进度的动态规划(如文献[7])不再适用,因此混合两种方向设计求解这类子问题的动态规划。给定某批L和一组{γsk},推广文献[14]的研究,首先将批L内的所有工件的加工工序从阶段1、阶段2...直到阶段S依次按照它们在批中的顺序进行排列。因此,每个工序x可能有多个紧前工序或紧后工序。然后,将由上述工序构成的优先级图转换成树结构:找到优先级图中最长有向路径,以其为主线,将所有与其相连的其他分支移到树的右侧。最后,根据形成的树结构,从后向前利用动态规划进行求解。
令x表示工序标号,X为批L内的工序总数,可知X=nL·S。将LRBf表示为关于工序的表达式,即
(11)
式中:
(12)
(13)
其中jx和sx分别表示工序x对应的工件和阶段。
令z1,z2,z3表示树结构中工序x的孩子,z1表示工件jx在紧后阶段sz1的工序,其集合表示为Ax;z2表示与jx属于同一批的且在批处理阶段的工序x的紧后工序;z3表示工件jx在紧前阶段sz3的工序,其集合表示为Bx。
因此,每个工序x的累计费用可表示为
(14)
计算得到最优费用后,再向前追踪得到对应批L的子问题的最优解。
对于分解后的F个子问题,每次迭代仅对一批L(L=1,…,F)执行上述过程,而对于其他批,则将子问题的解设为前一次迭代得到的值。因此,迭代F次,所有子问题才最优求解一遍。
2.3 异步次梯度优化
常规的次梯度算法要求每次迭代最优求解所有批级子问题[7,14],因此当问题复杂时,求解时间会较长,因此设计异步次梯度优化方法,每次迭代仅最优求解一个批级子问题,从而获得一个合理的异步次梯度方向。
异步次梯度定义为
(15)
算法执行过程中,首先,对一些参数进行初始化处理:令γ=0,通过最小化所有子问题得到初始的{cjs}的值,根据式(16)和式(17)更新乘子。然后,从第一次迭代开始,依次在每次迭代仅最优求解一个子问题,计算代理对偶值和异步次梯度,直至达到停止条件,算法停止。
(16)
(17)
其中:η为小于1的正数,β为步长,LR*由得到的最好可行目标值来估计,LDq为当前迭代的代理对偶目标值。
2.4 可行解构造
为得到原问题的可行解,对批处理阶段之前、批处理阶段、批处理阶段之后的工件加工,根据松弛问题的解和先前阶段的完工时间调整工件(或批)在该阶段的可能开工时间,按该时间的增序构造列表,然后根据该列表,依次将各工件(或批)分配到相应阶段可利用的机器上。
3 仿真实验
3.1 算法参数
文献[7]使用的常规的基于工件解耦和次梯度优化的LR算法(LR0)中,分解后的子问题仅包含单个工件的多个工序的优先级约束,即每个工序至多有一个紧前或紧后工序,采用前向或后向动态规划均可求解,待求解的子问题数为n,拉格朗日乘子数为S×K+n,求解子问题的动态规划的复杂度为O(2(S-1)K);文献[14]提出的基于批解耦和次梯度优化的LR算法(LR1)中,子问题数为F,所设计的LR&ISO算法(LR2)的子问题数为1,两者的乘子数均为S×K,动态规划的复杂度均为O(2(nf×S-1)K)。虽然LR1和LR2求解子问题的算法复杂度相同,但LR1每次迭代要优化的子问题数较多,导致消耗的总运行时间较长,而LR2每次迭代仅需求解一个子问题,因此多次迭代累加所节省的计算时间较为可观,同时由于它是近似求解松弛问题,故需要相应设计乘子更新策略来保证算法的收敛性。
考虑到LR0松弛的约束多会导致下界较松,且待求解的工件子问题也较多,因此本实验仅测试了LR1和LR2。当迭代数达到500或运行时间达到900 s时,程序停止。如果对偶间隙小于很小的数(0.5%)时,程序也停止。为公平比较这两种算法,以LR1的运行时间为停止条件运行LR2。
因为代理对偶目标值不是通过最优求解松弛问题得到,所以它不能作为最优费用的下界,因此,当迭代结束后,通过最优化所有子问题得到真正的下界,从而计算出真正的对偶间隙(表1中列LR2)。计算结果以(代理)对偶间隙(%)、迭代数和运行时间(s)来衡量,其中对偶间隙定义为历史上得到的最好上界与最好下界之间的相对差,并转化成百分比的形式;代理对偶间隙(表1中列LR′)定义为历史上得到的最好上界与当前代理对偶目标值之间的相对差,并转化成百分比的形式。利用C语言对两种算法进行编程,在Windows 7操作系统(64位)的计算机(Intel Core i5-5200U 2.20 GHz 2.20 GHz)上运行。
3.2 实验一
利用文献[17]的宝钢实际生产数据产生实验所用各种数据。炉次(工件)数设为12,加工阶段为3(炼钢,连铸,热轧),浇次(批)数为{3,4,6},每阶段的机器数取自{3,4,5},计划时间范围K设为8小时(480 min)。wi、Pij、Ri、Tj,j+1、STij分别满足[10,15]、[30,50]、[1,10]、[20,30]、[15,25]之间的均匀分布。共测试了9种规模,每种规模随机产生10个实例,因此,本实验测试了90个问题实例,表中的每个值(除最后一行)为同一规模的10个实例的平均值。
表1列出了测试结果。从表中结果可知:
(1)由LR1和LR2得到的平均对偶间隙分别为0.39%和0.48%,均小于0.5%,因此两种算法求解小规模实际问题时都能得到非常接近最优解的近优解。在LR2中,平均代理对偶间隙为0.47%和真正对偶间隙相差0.01%,两者相差不大。
(2)LR1和LR2所使用的平均运行时间分别为8.79和6.39秒,迭代数分别为185.62和608.47,因此,所提出的LR2在求解速度方面明显优于LR1,即在较短的时间内得到了高质量的近优解。
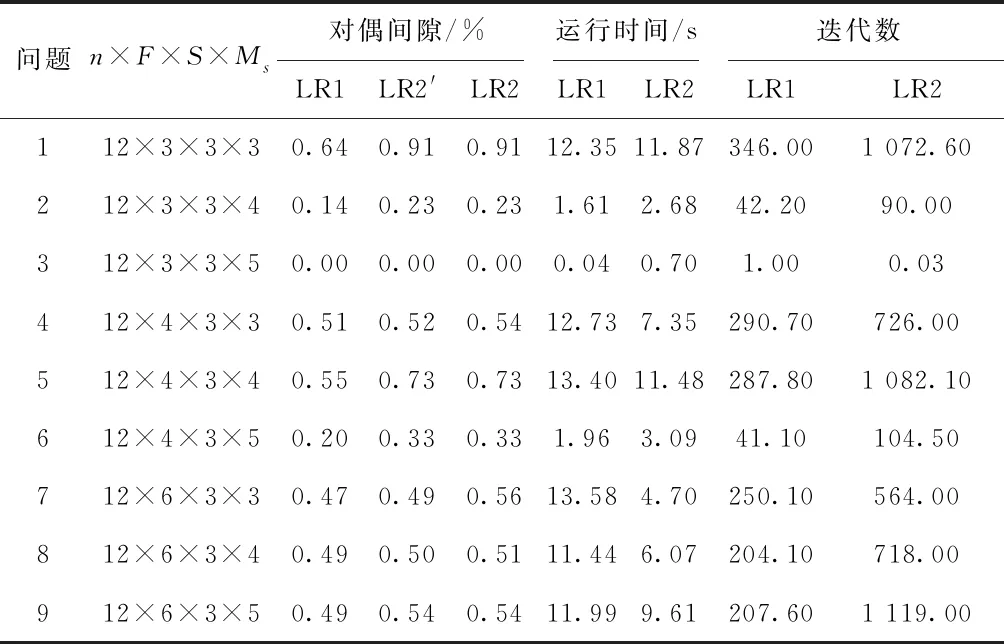
表1 n=12的测试结果
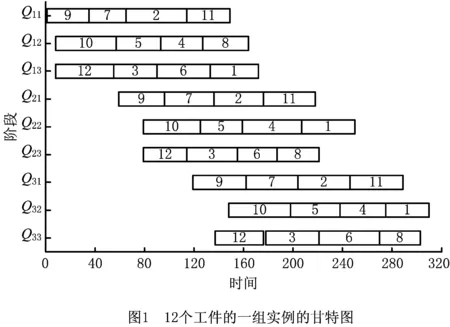
以上述问题12×3×3×3的一个实例为例,各工件的加工时间、释放时间、权重、调整时间如表2所示,相邻两阶段的传送时间分别为22和23,已知在批处理阶段各工件的组批顺序(10→5→4→1,9→7→2→11,12→3→6→8),运行LR&ISO算法,可得到如图1所示的甘特图,最小总加权完成时间为37224,对偶间隙为0.70%。
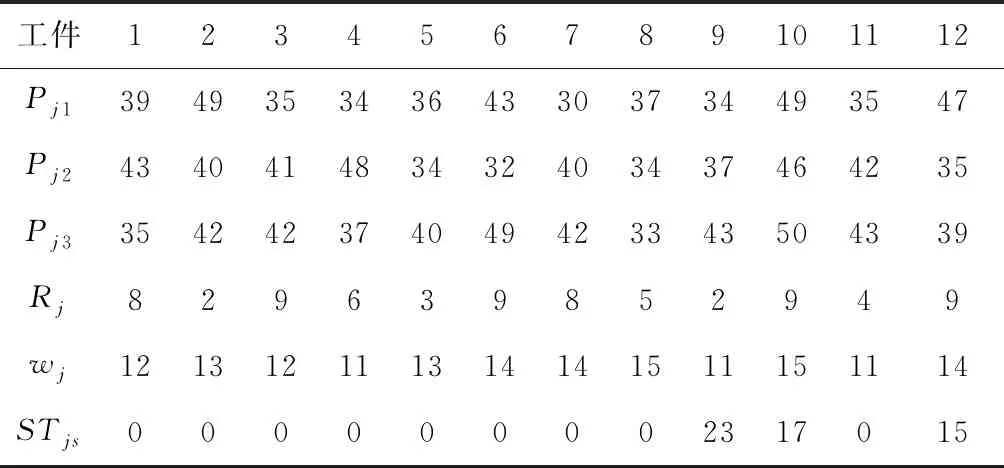
表2 各工件的参数设置
3.3 实验二
本实验测试了工件数为{24,36,48,60,84}的实例,数据随机产生如下:
(1)S∈{3,4},Ms∈{3,4,5},nf∈{2,3,4};
(2)工件j的权重wj和加工时间Pjs满足[1,10]的均匀分布,Rj满足[1,5]的均匀分布;
(3)Ts,s+1和STjs分别满足[4,6]和[3,5]之间的均匀分布;
(4)计划时间范围K设置为所有工件加工时间之和。
因此,本实验共测试了5×2×3×3×10=900个实例,测试结果如表3~表7所示。
从表中结果可得到以下结论:
(1)对n=24,36,48,60,84的情况,由LR1得到的平均对偶间隙分别为1.41%,2.03%,2.69%,4.47%,13.16%;由LR2得到的分别为1.51%,1.62%,1.85%,2.16%,3.49%。除了n=24时LR2表现略差于LR1(相差0.1%),对于其他规模问题,LR2均明显优于LR1,而且在解的质量方面的优势随问题规模的增大而增加。因为对偶间隙是由启发式解和下界之间的相对差计算得到,所以对偶间隙小于3%的解非常接近最优解,因此,总体来看,由LR2可得到质量更佳的近优解。
(2)在相同的运行时间内,对于不同规模问题,LR2执行的迭代数分别为LR1的7.32,12.15,17.33,20.83,27.32倍,因此,随着问题规模的增大,所设计的LR2迭代次数要多的多,这是由于LR1每次迭代最优求解所有批级子问题使得每次迭代运行时间长从而导致迭代次数少。
(3)对不同规模问题,由LR2得到的代理对偶间隙分别为1.47%,1.55%,1.71%,1.92%,2.75%,与真正对偶间隙分别相差0.04%,0.07%,0.14%,0.24%,0.74%,两者差距随问题规模的增大呈递增趋势,但总体来看,相差不大。
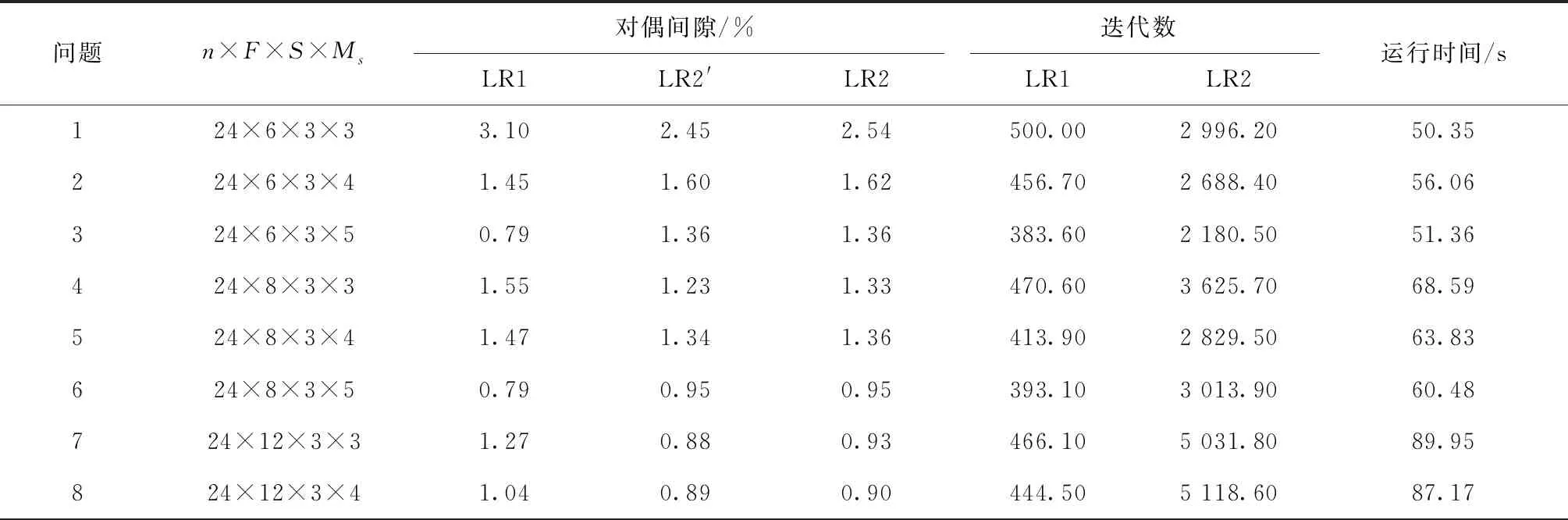
表3 n=24的测试结果
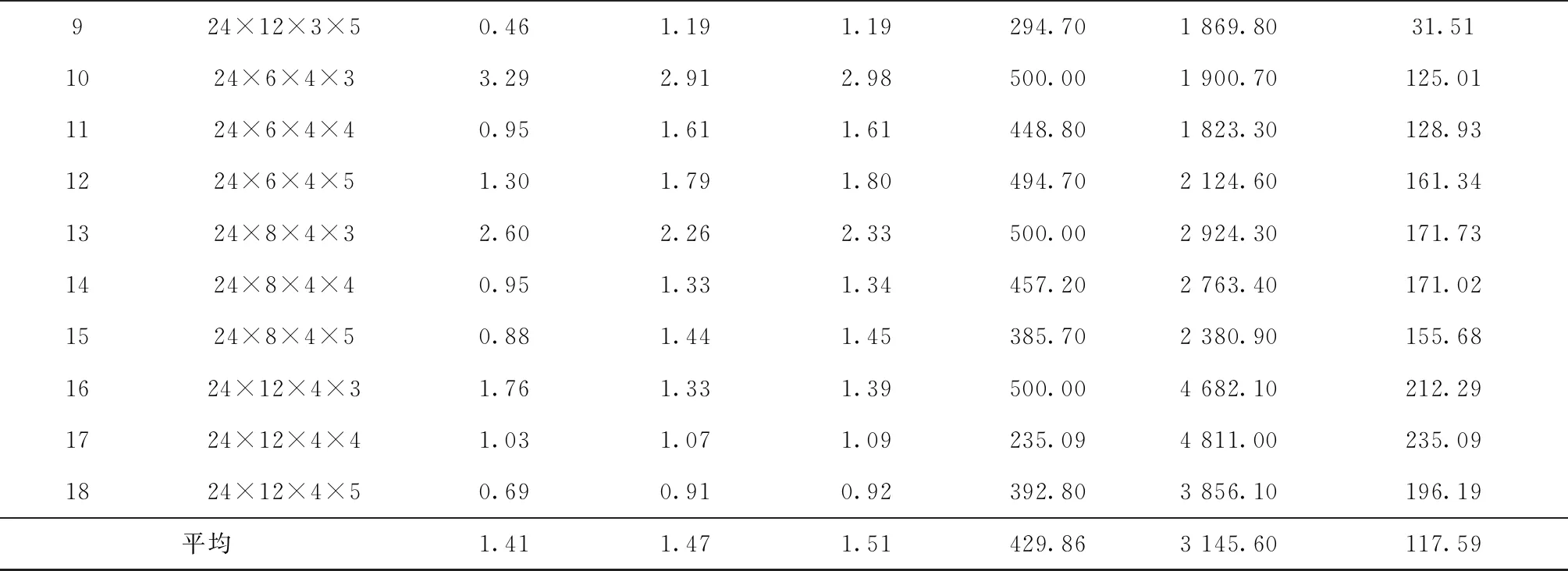
续表3
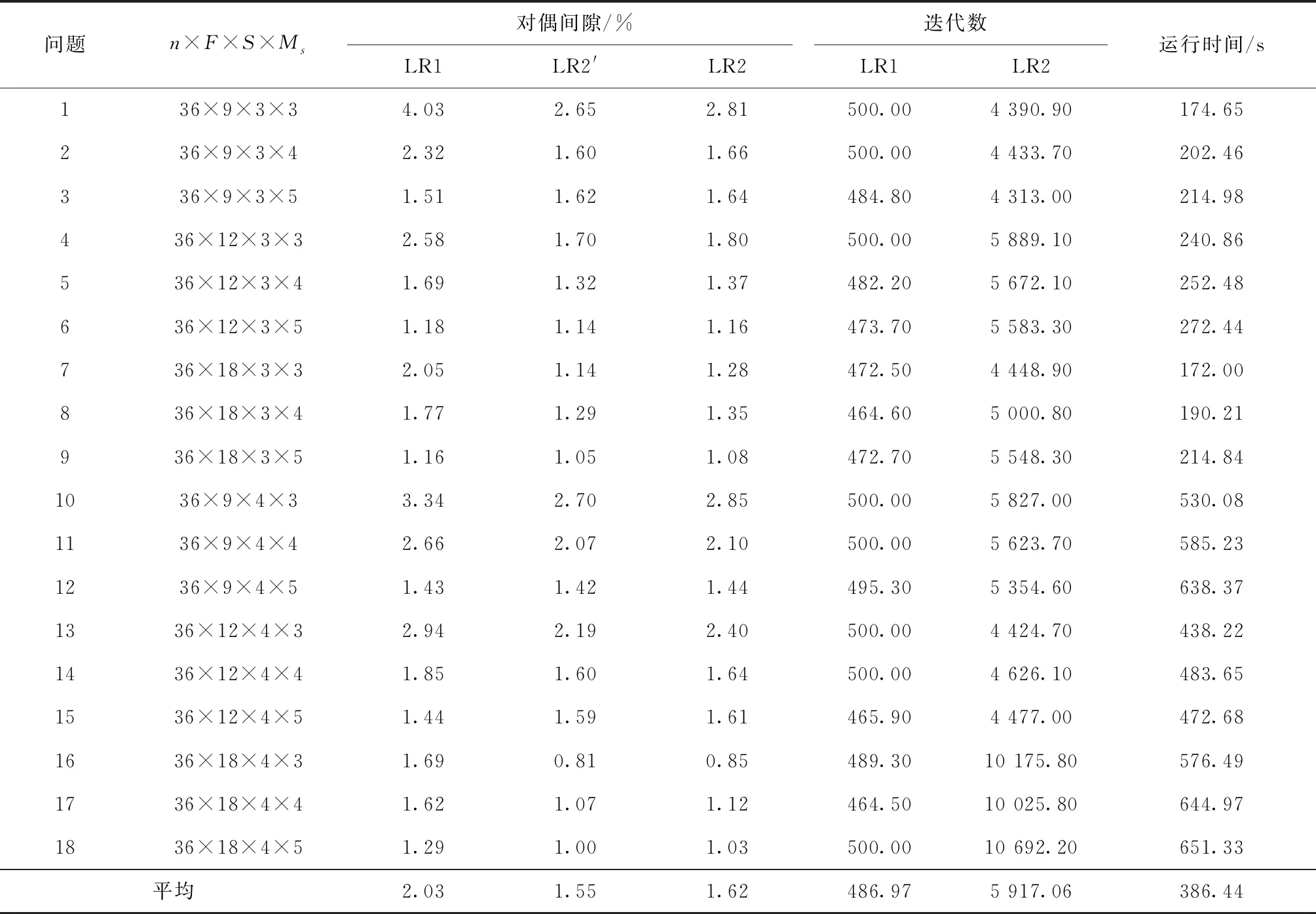
表4 n=36的测试结果

表5 n=48的测试结果
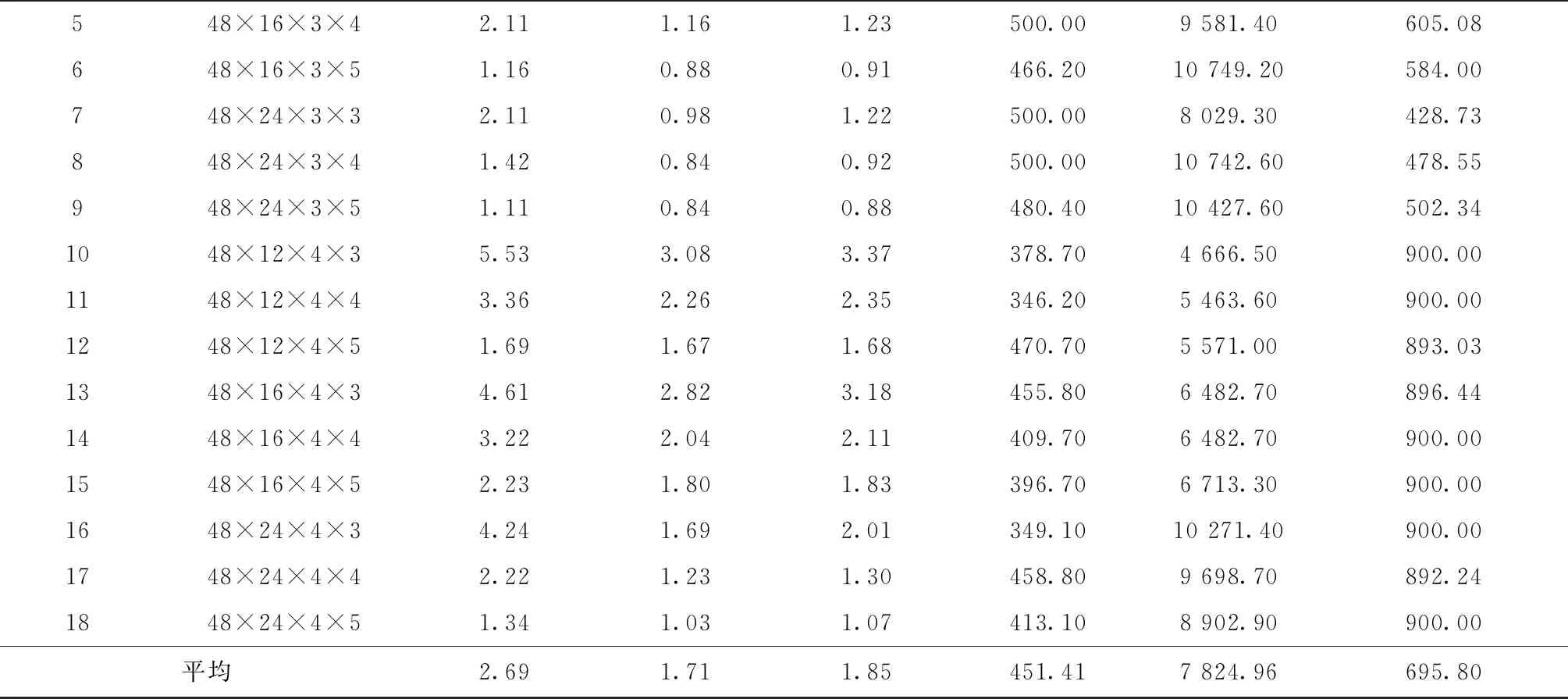
续表5
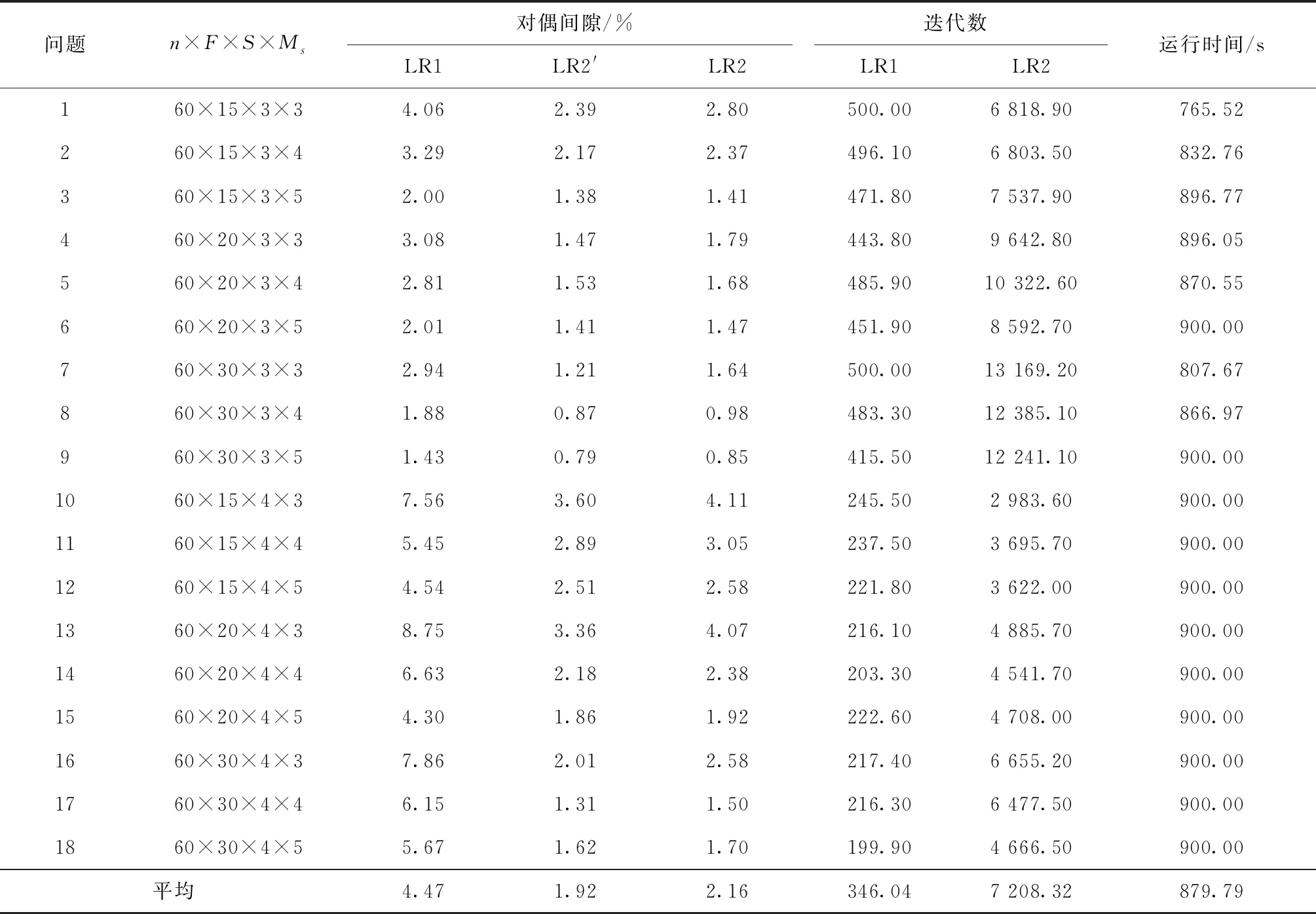
表6 n=60的测试结果

表7 n=84的测试结果
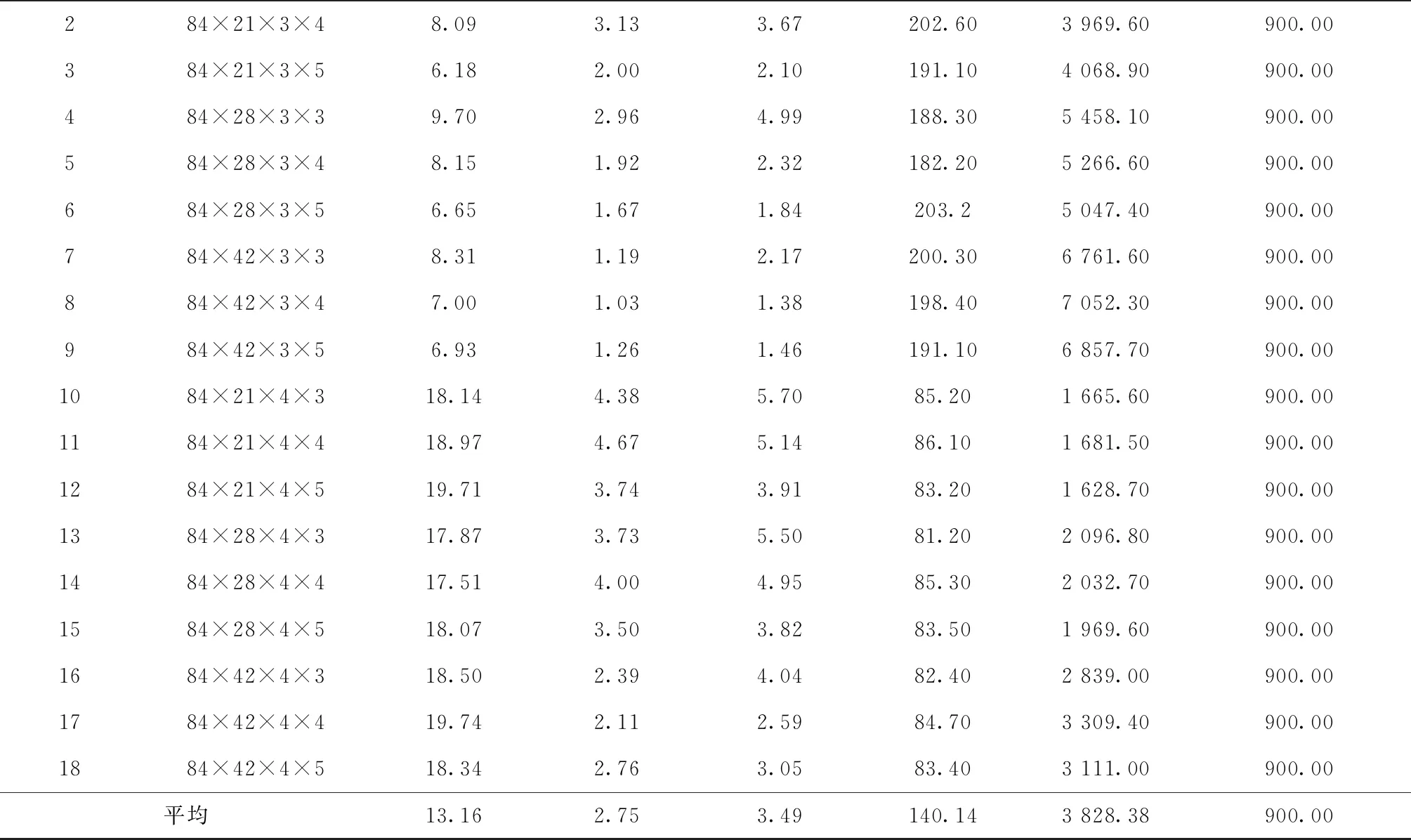
续表7
4 结束语
本文提出了LR&ISO混合算法求解多阶段含离散机和批处理机的FFSP。基于子问题异步求解策略,该算法每次迭代仅最优求解一个批级子问题,使得迭代时间有大幅度缩短,这对实际生产尤为重要;为得到合理的乘子更新方向,利用异步次梯度优化计算下次迭代的乘子。通过对实际生产数据和大量随机数据的实验测试,验证了引入异步求解策略的LR&ISO算法不但解的质量较好,而且求解速度较快,尤其是求解大规模问题时,它在各方面的表现均明显优于基于批解耦和次梯度优化的LR算法。
未来可将LR&ISO算法应用于具有其他生产特征的FFSP,由于该算法适合于求解“可分离”的数学模型,且求解过程中某些参数如步长等要根据具体问题进行调节,因此,对于其他类似问题,还需根据所研究问题具体设计该方法的应用方式,以获得更佳的近优解。
