舰炮射击指挥员指挥决策过程混沌建模与分析*

杨绍清，陶中韬，黄义

(海军大连舰艇学院，辽宁 大连 116018)

0 引言

随着以信息技术为核心的新军事革命的发展，战场环境开始复杂多变，战争进程变得迅猛快速，作战样式与战场环境对舰炮射击指挥员也产生了很大影响。虽然在科学技术的推动下，武器装备性能大大提高，运用手段日趋多样并被不断优化[1]，训练方式趋于科技化、高效化[2-3]，自动化决策方式和辅助手段受到日益广泛关注[4-7]，但人始终是战争中的重要因素，也正是这个原因，针对人的因素和人在系统中表现的研究也成为在新形势下的研究热点[8-9]。舰炮射击指挥员在充分发挥舰炮武器系统的作战效能中起着至关重要的作用。因此，在现代化的海战中，舰炮射击指挥员将面临前所未有的挑战。这就要求一般作战指挥员要有充足的知识准备和经验准备[10]，同时还要有良好的心理素质和思维习惯，加强对舰炮射击指挥员决策过程机理的研究，将有利于提高指挥员的决策能力，从而提高部队战斗力。

混沌理论主要用于研究非线性系统演化过程的行为特征，在心理学领域有着重要影响，能够得出更接近复杂的心理活动的研究结果[11]。本文利用Lefebvre[12]混沌心理模型、结合舰炮射击指挥过程，建立了射击指挥员决策过程的数学模型，深入分析了射击指挥员决策过程机理，并提出了提高指挥员决策水平的途径。对于研究舰炮射击指挥员决策问题将具有一定的参考价值。

1 指挥员决策模型及机理分析

1.1 射击指挥员主要决策环节与节点的描述

舰炮射击指挥是指舰炮对目标实施炮火攻(抗)击活动中由射击指挥员指挥决策并负责指挥实施的过程，其指挥流程的通畅与否直接影响着舰炮作战使用效能的发挥。舰炮射击指挥一般过程和内容为：接收作战任务；接收目标指示；选择目标观测方式；选择弹种和引信；确定指挥仪工作方式；确定射击方式和射击方法；确定舰炮发射方式和发射速度；实施开火、转火和停火等[13]。

一般情况下,每个过程节点中有多种方式供指挥员决策选择，比如在接收作战任务时可以使用人工、自动；在接收目标指示时可以使用自动、半自动或人工[13]；选择目标观测方式中，如对岸上目标射击时，可以选择炮位光电瞄具或炮外光电跟踪仪等[14]；根据不同情况的工作效果确定指挥仪工作方式[15]；确定射击方式可以使用集火射击和瞄准点均匀分布射击方式[16]；确定射击方法，可以使用传统的测量距离方向法，和各种新的方法如基于舰位经纬度坐标的舰炮对海上目标射击校正新方法等[17]。愈发多样的选择要求指挥员能够在给定时间内尽快做出正确决定[18]。

上述各节点的选择结果可以简化为二元选择的情况，用“1”表示选择正确，“0”表示选择错误。因此，深入分析单个节点的决策过程更加重要。

1.2 单节点指挥员决策混沌模型

指挥员单节点决策过程可以利用心理学的相关理论来进行建模与分析[12]。舰炮射击指挥员的决策结果主要受到指挥员的无意识(subconscious)、有意识(conscious)和动机(motive)3个因素的影响。所谓无意识，是指指挥员没有觉察到的心理活动，或者与常规的行为准则冲突而被自觉压抑的想法，侧重于指挥员的本能行为。有意识则是指挥员利用相关理论知识对战场态势觉察到的、有目的的、自觉的、主动性的判断。无意识和有意识都是指挥员对战场环境、敌我态势进行思维决策的结果，是一个连续过程。无意识能够让指挥员自动地屏蔽大多数无用信息，选择正确信息通向意识，因此无意识也是非常强大的。动机则是由目标或对象引导、激发和维持个体活动的一种内在心理活动过程或内部动机。

假设：x1表示指挥员无意识选择正确的可能性；x2表示指挥员有意识地利用先验知识选择正确的可能性；x3表示指挥员个人动机正确的可能性，即决策的目标是正确的可能性；f(x1,x2,x3)为最终选择正确的可能性。如果，x1,x2,x3中的任意2个固定不变时，第3个变量对决策结果的作用是线性的，则有

f(x1，x2，x3)=a0+a1x1+a2x2+a3x3+

a4x1x2+a5x1x3+a6x2x3+

a7x1x2x3.

(1)

为了能够确定式(1)中的待定系数ai(i=1,2,…,7),先给出3个心理学中的公理[5]：

(1)f(0,0,x3)=x3,∀x3∈[0,1],

(2)f(0,1,x3)=0,∀x3∈[0,1],

(3)f(1,x2,x3)=1,∀x2，x3∈[0,1].

3个公理来源于道德体系。第1个公理意思是，当外部信息倾向于指挥员的无意识采取错误决策(x1=0),指挥员也有意识要采取错误决策(x2=0),那么指挥员将对他的决定负责，最终的结果取决于指挥员的动机；第2个公理意思是，当外部信息倾向于指挥员无意识采取错误决策时(x1=0),但指挥员有意识选择正确的决策(x2=1)，那么，指挥员屈从于外部信息无意识的压力，最终选择错误决策；第3个公理意思是指指挥员的本意都是正确的，因此，当外部环境促使指挥员的无意识选择正确决策(x1=1)时,指挥员仅能够采取正确决策。

通过上述3个等式，可以解出a0=0，a1=1，a2=0，a3=1，a4=0，a5=-1，a6=-1，a7=1。从而

f(x1，x2，x3)=x1+(1-x1)(1-x2)x3，

(2)

式中：x1，x2，x3∈[0,1]。可以看出，指挥员的决策受到无意识的影响很大，当无意识做出决策x1=1时，则最后决策为1；当无意识决策为0时，此时有意识x2和x3动机将发生作用。

2 指挥员决策模型分析

一般地，指挥员进行决策时，在同一时刻仅能够考虑2个因素的作用，而式(2)中有3个变量，这就需要寻找一种新的函数形式，即对函数f进行变换。因为x1,x2,x3∈[0,1]，所以(x2，x3)∈[0,1]。数学上可以证明，函数f可以被表示成

f(x1,x2,x3)=fs(x1,fs(x2,x3)).

(3)

式(3)是一种递归形式，其中fs的形式是唯一的，有

fs(x,y)=1-y+xy,

(4)

则可以得到fs(x2,x3)，即

fs(x2,x3)=1-x3+x2x3.

(5)

fs(x2,x3)具有自反射的作用，假设：

(1) 指挥员以以往的经验来判断，外部信息将促使他有意识地选择正确决策x2=1，指挥员动机也选择正确决策x3=1，则有fs(x2,x3)=1，表明指挥员认为自己是在积极行动。

(2) 前面已经分析，如果外部信息促使指挥员无意识地选择错误决策，即x1=0，指挥员有意识地选择正确决策x2=1，则在第1次进行决策时指挥员最终将选择错误决策f(x1,x2,x3)=0；当下一次相同的情况出现时，指挥员将会根据第1次决策的经验有意识地改变本次的决策，即x2从1变为0，如果指挥员的动机仍然是正确决策x3=1，则自反射的结果为fs(x2,x3)=0，如果外部信息敦促指挥员无意识地选择错误决策x1=0，则最后的选择为积极行动f(x1,x2,x3)=1。在第1次决策中，指挥员认为自己是积极的，但执行了一个错误决策；在第2次决策中，指挥员认为自己是消极的，实际上却执行了一个正确的决策。可见，fs(x2,x3)具有帮助指挥员自我思考的作用，当他意识到自己消极时，能够阻止选择消极行动。

尽管式(3)表明了指挥员决策具有非线性，但指挥员的动机x3不会表现出很强的非线性行为，所以指挥员的动机可以不作为输入，至少不作为一个明确的输入。这样，决策结果可以用无意识和有意识2个参数来表示。

设射击指挥员是现实的，其动机是积极的，但客观上的结果可能是正确的，也可能是不正确的，所以可以设定最后的决策为x3，这样就可以用一个新的函数fr(x1,x2)来取代式(2)中的变量x3和决策结果，得到

fr(x1,x2)=x1+(1-x1)(1-x2)fr(x1,x2).

(6)

当x1+x2>0时，则有

(7)

式(6)在x1=x2=0时是不确定的，表明外部信息以最大的压力促使指挥员选择错误决策。当时x1，x2→0，函数fr(x1,x2)∈(0,1)。

式(7)描述了舰炮射击指挥员在某一时刻选择正确决策的可能性，但是，函数fr(x1,x2)是静态的，没有给出决策随时间变化的可能性。假如指挥员做决策的时间受外界影响，必须提前做出决策，可以通过思考变量x1和x2当时的可能行为而推断出关于当时的发展状况。变量x1与指挥员对其所处环境的一种本能上的感觉有关，x1是一个无意识的函数，也是对瞬间发生事情的一般想法；变量x2与指挥员有意识的思考有关，暗示着需要对决策结果的发展进行时间分析，由此，x2可以表示为

x2(t)=x2(0)e-λt+x2(∞)(1-e-λt)=

x2(0)+{x2(∞)-x2(0)}(1-e-λt),

(8)

式中：参数λ代表指挥员对于决策方案进行思考、分析的响应参数，它决定指挥员做出初始决策x2(0)到最终决策x2(∞)的速度。那么，射击指挥员所做出的决策随时间而发生的变化可将式(7)进行求导获得

(9)

将式(8)代入式(9)，可得

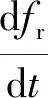
(10)

公式(10)的限制条件为：x1=1或x2(∞)=0。

式(10)是Logistic方程，指挥员响应参数λ变为分岔参数。可见，射击指挥员在进行决策的过程中，由于大脑神经元脉冲的离散特点，用离散形式比用连续形式更能合理地描述大脑的功能。假设大脑是神经元的集合体，那么在处理和进行决策过程中，神经元可以通过发射或不发射脉冲的形式自主地选择正确决策或者错误决策，函数fr代表任一时刻选择正确决策的可能性。更进一步假设，这些神经元通过某种复杂的方法联系在一起，相互之间的作用遵循某些规则，即：一个神经元在下一个离散时刻是否发射脉冲，仅取决于与它所相连的神经元在前一时刻是否对它发射脉冲的情况。这样，对于0和1之间的任一初始值fr(0)，神经元的发射过程将会产生一系列的fr(i)，最终可能出现下面几种情况：

(1)fr(i)收敛于一个不动点；

(2)fr(i)会聚于一个有限的循环；

(3)fr(i)成为无序的混沌序列。

第1种情况能够给出一个比较好的决策时机，而后2种情况没有明显优化的决策时机，这就是射击指挥员在决策过程中的犹豫现象。

式(10)使用的限制条件x2(∞)=0是期望的结果，正好与式(5)中第2次决策的期望结果是一致的；而限制条件x1=1表明了无意识赞同选择正确决策，可以推测这一条件可能导致指挥员决策时的犹豫，面临着决策正确但难以实现的情况。

为了更好地解释上述分析，将式(10)离散化，可得

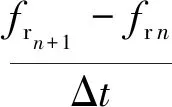
(11)

通过对式(11)进行变换，可得

(12)

式中：r=λΔt,λ为响应参数，Δt为采样周期。采样周期保持原来的状态，当采样周期过长时，会影响指挥员的决策结果，产生混沌现象。

3 仿真分析

将系统方程(12)进行仿真，得其仿真结果如图1所示。

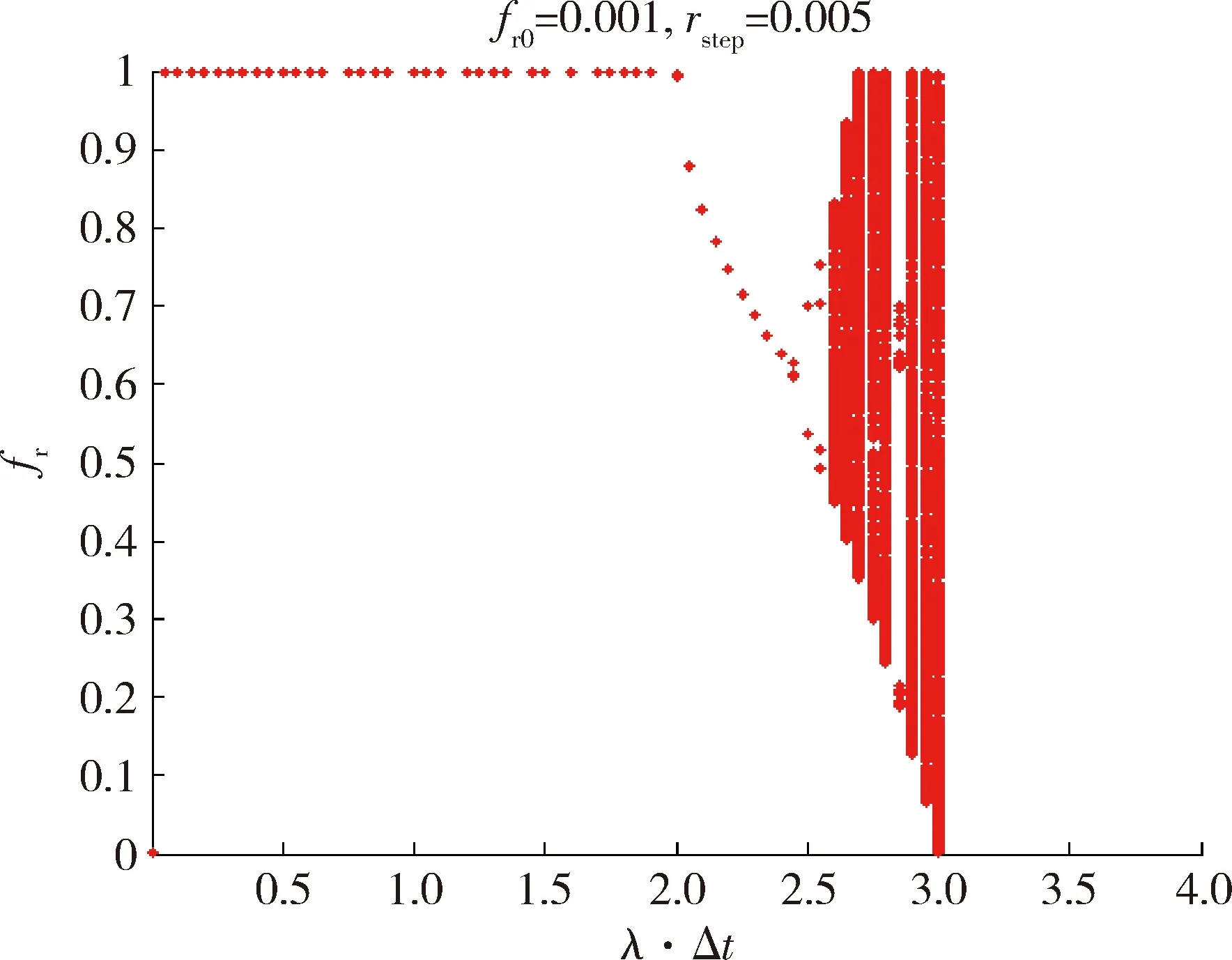
图1 仿真结果

图中，初值设定为fr0=0.001，步长rstep=0.005。对于不同r的的值，系统方程(11)呈现不同的特性，随着r值的不断增加，系统将不断经历周期分叉，最终达到混沌。

当0

当r=2时，系统的稳态解为周期2，出现2分叉现象；

当r=2.449 489时，系统的稳态解分叉周期为4，进而产生无序的混沌序列。

由图1可知，仿真结果与神经元的发射过程产生序列的可能出现的3种情况相一致。

由于r=λΔt，λ代表了一次决策过程中指挥员决策变化的速度；采样周期Δt代表了指挥员2次决策之间的间隔时间；r实际上代表了指挥员在2次决策中经历的决策结果数量，体现了指挥员给出最终决策的离散程度，当r<2时离散程度较小且具有唯一的决策结果，当r≥2时离散程度较大且具有多个决策结果，所以当r≥2.449 489时，指挥员的决策过程是混沌的。

4 结束语

通过上述分析可知，在舰炮射击指挥过程中，指挥员主要受到无意识和有意识决策过程的影响，最终的决策行为可能会分叉或产生混沌现象，是否会出现混沌与指挥员的决策响应参数λ有关，并对应着指挥员出现的犹豫不决现象。要减少这样的现象，可从以下几个方面对射击指挥员进行专门的培养和训练：①坚持理论和实践相结合，射击指挥员要深入研究射击指挥中涉及的决策问题，掌握各种方法、方式的使用特点和使用时机；②能够获取准确、完整的战场态势信息，射击指挥员必须能够掌握装备的信息显示方法、内容和含义，学会对重要信息的提炼和加工方法；③注重提高射击指挥员快速决策能力，特别是无意识下的决策能力。

舰炮射击指挥员的指挥决策过程是一个非常复杂的过程，本文将混沌心理模型运用于指挥决策过程的分析中，强调了实践环节训练的重要性，提出了训练的最高标准是指挥员能够“本能地”做出正确的决策，对决策指挥系统仿真和射击指挥员的培养训练具有一定参考价值。