基于Elman神经网络的流体管道泄漏点检测定位

曹峥，邓建强，王泽良，宣炳蔚，郭希健

（1.西安交通大学，西安 710049；2.陕西省能源化工过程强化重点实验室，西安 710049；3.上海电气电站设备有限公司，上海 201100）

流体管路输运是过程工业中的关键流程，对于实现能源资源的传输环节，具有不可替代的作用。我国是能源消耗大国，油、气、水等资源分布具有较大的地域跨度性，需要长期依赖管道输运。当前，全国油气输运管道总里程已超过12万公里，预计到2025年，全国油气管网规模将增加1倍[1]。在管线建设不断推进的同时，管龄增长、环境影响、腐蚀及意外破坏等因素不容忽视。据统计，50%地下管道的管龄已超过30年[2]，管道泄漏时有发生，造成了巨大的资源浪费和经济损失。由于管道漏损监测和防控意识的薄弱，我国城市供水管网平均漏失率超过14%，因供水管网漏失导致的年损失水量超过 60亿立方米[3]。石化等行业的长输管道泄漏事故，还将严重威胁群众生命安全，危害周边环境。

管道检测技术是一种针对管道输送系统开展异常状态监测、识别与定位的故障诊断技术。目前，针对管路泄漏的检测与定位处于快速发展时期。按照检测方式，可分为直接检测和间接检测两类方法。人工巡检是一种最简单的直接检测方法，其需要依赖大量的人力，难以实现快速覆盖。随后出现的示踪法通过向管内注入放射性示踪剂或异味气体开展检测，但同样面临不够灵敏、无法开展实时监控等适用局限性问题。管内探测法通过在管道内部放置特定的探测设备，使其沿管移动，实现对泄漏点的准确探测，但检测周期较长，且只适用于结构简单的长直管路。热红外成像方法通过感知管道泄漏点周围环境温度来快速探测泄漏位置，对于深埋地区（如海底管道的检测中）难以适用。后续，人们通过在管道周围布设光纤传感器实现了针对难以探测的小泄漏及缓慢泄漏的检测，但光纤检测成本高昂，限制了该技术的大规模应用。

间接检测法主要基于流体的状态开展检测，最为常见的是压力梯度法和负压波法。压力梯度法通过基于管线多个压力测点的压力梯度变化曲线相交位置来大致推断泄漏位置，虽然原理简单，但较难实现准确定位。负压波法通过捕捉管道泄漏后，负压波传播至两端的时间差来实现定位。由于其具有成本低、易维护、检测精度高等优势，在长输管道泄漏检测领域获得广泛应用。张红娜[4]在负压波技术中引入广义模糊双曲正切模型对管道进行模式识别，利用负压波检测实现准确定位的同时，又消除了单纯负压波检测存在的高误报率问题，但该模型中的前提参数及结论参数都需要结合全面的样本数据进行辨识。Liu等[5]通过实验研究了负压波方法在天然气管道检漏中的应用，结合改进小波分析模型来识别压力信号实现泄漏点的定位。Gao等[6]基于压力波动信号提出了时间延迟估计的分化改进方法，利用模式识别消除低频干扰下的信号失真。针对负压波法对小泄漏信号的探测不敏感问题，一些学者将低频声波和负压波相结合，实现了定位精度和小泄漏量的识别提升[7-8]。然而负压波与声波都属于一种压力扰动，具有相同波速，仍然无法应对缓慢泄漏情况的检测。针对信号噪声问题，实践中常采用小波技术进行信号消噪，捕捉奇异点以实现泄漏点定位，但只是准确发现了负压波出现时间，仍然无法有效消除工况变化的干扰。阚哲等[9]提出信息物理系统架构进行分支管道泄漏定位的方法，把压力信号拐点时刻作为特征样本，利用双支持向量机学习开展管道泄漏点定位。王剑锋[10]提出了基于负压波检测的管道泄漏监测系统，利用相关分析的互相关算法得到时间差，实现了准确的仿真计算定位。该法适用于瞬时捕捉突发或大剂量泄漏，定位准确度需要高度依赖波速等变量信息。

图1 常见管道泄漏检测方法分类与比较Fig.1 Classification and comparison of common pipeline leakage detection methods

对常见的管道泄漏检测方法进行比较，如图1所示，各方法均存在不同的优势和缺陷。基于负压波的检测技术，整体上具有较好的应用性和经济性。其灵敏性和定位精度的不足，虽然可以结合其他手段进行弥补，但是只能预先在泄漏前进行被动式检测，即使准确捕捉到了奇异点信号，也需根据常规一维模型中的定常波速、给定物性等先验参数求取定位，对于规模大、复杂性高、变量多、存在缓慢漏失等情况的管网，依然存在检测定位困难。文中基于管路内部流体的压力波动特征，采用基于负压波方法开展了泄漏点的理论计算，结合负压波的特征采集方法，探讨了反馈型Elman人工神经网络的智能算法预测，完成了相应的泄漏检测定位工作，从而验证了人工智能方法在管路泄漏定位问题中的准确性与有效性。

1 检测原理

1.1 负压波

利用负压波进行检漏定位是基于管道内流体压力波传播特性开展的，其原理如图2所示。管道发生泄漏时，泄漏口瞬间泄压，形成负压波，沿管道两端传播。通过在管道两端采集压力脉冲信号，结合负压波的波速等参数信息，便可对泄漏位置进行定位。

图2 负压波检漏定位原理Fig.2 Principle of negative pressure wave leakage detection and location

利用负压波法开展管道检漏时，负压波波速的求取是非常重要的一步，考虑到其在含有多种管件或流体介质不同的管网中的传播较为复杂，利用式（1）—（3）对波速进行估算[11]：

式（1）中：c为负压波速，m/s；αp为气体压缩系数，Pa-1；ρ为流体密度，kg/m3；D和e分为壁厚和管内径，m；E 为管弹性模量，Pa。

式（2）中：X为泄漏点距管路上游端的距离；Δt为上下游压力测点检测到负压波的时间差，s；L为管长，m。当负压波速c远远大于流体流动速度v时，式（2）可简化为：

1.2 Elman神经网络方法

Elman神经网络属于一种反馈型神经网络，该网络结构能在有限时间内逼近任意函数，其动态记忆性使其具有时域和空域模式的学习能力，对于时序预测问题及复杂网络的数据处理具有很好的解决能力。该神经网络的拓扑结构如图3所示。其通过在隐含层网络中增加了一个承接层，使其作为延时单元，将上一时刻的隐层状态进行记忆存储，并连同当前时刻的网络输入一并作为新的隐层输入，这一局部回归特点使得该网络对历史数据具有更好的敏感性。

图3 Elman神经网络拓扑结构Fig.3 Elman neural network topology

Elman神经网络的主要模型公式可以表示为：

式（4）—（6）中：y表示输出层向量；xj表示输入层向量；hi表示隐含层向量；ci表示承接层向量；G(·)、F(·)分别为输出层和中间层的传递函数，在文中，分别选取为purelin线型函数和 logsig非线性函数；w1、w2、w3为连接权值；t和t-1代表当前和上一时刻的神经网络状态。

2 仿真分析

2.1 模型计算结果

文中建立的模型结构为T型管路，如图4所示。管道为弹性管道，粗糙度为0.025 mm。长直管线总长1100 m，管径为50 mm，T型管路支路模拟泄漏路径，孔径为10 mm。管道上游恒压水箱水头高度为 120 m，下游水箱与大气连通。利用球阀开启模拟泄漏发生情形，在与上下游水箱相距5 m处，采集压力信号，用于数据分析。采用Flowmaster软件开展数值仿真，模拟不同位置发生泄漏的情形。为了简化起见，在此设置波速为1000 m/s开展仿真计算，而在实际开展泄漏位置检测时，波速值存在不确定性，需要估测。管道输运过程的仿真时间为25 s，设定10 s时刻发生泄漏，计算步长设为0.01 s。为了考虑实际工况中的噪声情形，对于每次采集到的压力信号叠加一组均值为1 kPa、方差为0.1的随机噪声信号。

图4 管道泄漏仿真模型Fig.4 Pipeline leakage simulation model

以在泄漏点为800 m时的工况情形为例，利用负压波法进行泄漏定位。由于压力测点含有随机噪音，故采用 db6小波函数对信号进行三层分解，随后完成低频系数重构，提取压力采集信号降噪后的奇异点信息。管道上游压力波动信号经过小波变换后的效果如图5所示，纵坐标x表示原始信号，d1—d3表示高频系数重构结果，a3为经过小波包分解后第三层低频系数的重构结果。从图 5可以发现，该去噪后的信号变得光滑，方便更好地观察到奇异点等波动信号特征。

图5 管道上游压力波动信号的多层小波分解重构Fig.5 Multi-layer wavelet decomposition and reconstruction of upstream pressure fluctuation signal of pipeline

对管道下游采集到的压力信号进行同样的小波变换后，可以得到负压波传播到下游的时间。在此算例中，所得到的管道上、下游负压波捕捉时间差为Δt=0.49 s。此处波速采用与仿真中设置的值计算，代入式（3）可求得泄漏点的位置在X=795 m处。

与传统的负压波检测方法相比，利用Elman神经网络对泄漏位置开展定位，无需求取波速等未知参数。此方法需先确定特征样本作为输入向量，进行神经网络的训练。对于压力波动信号而言，常用的波动特征包括均值、方差、波距、偏斜度、峭度、幅值等。由于文中主要为方法性介绍，泄漏工况为瞬时泄漏，故采用负压波到达上游压力表的时间及到达两压力表的时间差作为特征输入向量，泄漏点位置作为输出向量，将泄漏位置为335～800 m范围内的30组数据作为神经网络的训练样本。利用 matlab程序创建包含40个神经元，延迟层向量为1:3、反向传播网络训练函数为traingdx的Elman网络，随后开展学习训练，得到回归性能曲线（如图6所示）。可以看出，相关系数为0.998 94，说明训练输出值与样本目标值符合情况较好。

图6 网络训练过程的回归性能曲线Fig.6 Regression performance curve of network training process

利用训练好的网络开展泄漏数据的仿真测试，选取5组数据作为测试样本，求得的泄漏点位置见表1。其中前2组数据使用了训练集中的样本数据，后3组数据为新的插值或外推样本数据。可以看出，利用经过训练的神经网络对泄漏点的预测整体较好，最大测试误差为1.83%，可以满足工程定位要求。

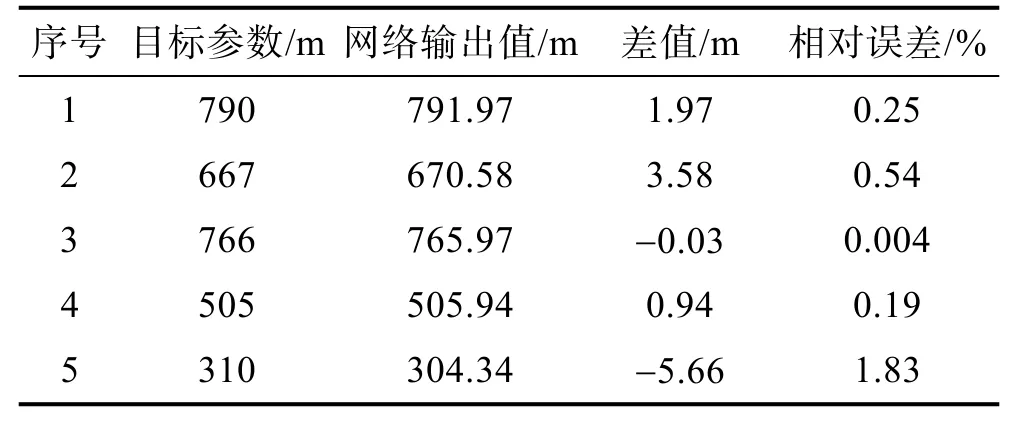
表1 基于Elman神经网络的泄漏点预测结果Tab.1 Prediction results of leakage point based on Elman neural network

2.2 算法验证

为了验证文中定位算法的有效性，基于文献[12]中的液体管线泄漏台架实验系统进行建模，对比了实验数据、负压波法及运用神经网络方法的泄漏点定位结果。设置验证模型测试段的管长为245.18 m、波速为2080 m/s、操作压力为3 MPa进行仿真后，通过不同方法进行泄漏点定位的计算结果如图7所示。

图7 泄漏点定位计算结果对比Fig.7 Comparison of calculation results of leakage point localization

由 P1—P4压力测点构成的三组测压区间中，实际泄漏点位置分别为125.65、125.65、38.3 m，由负压波法公式（1）计算得到的波速为 1446.2 m/s，与实测波速相差较大。文献[12]中采用了负压波修正波速的方法来提高定位精度。经与实际泄漏位置对比，基于Elman神经网络方法的定位误差最大为2.2%，整体准确率较高。

3 结语

文中采用基于传统负压波的方法及人工智能方法开展了针对水力输运管道的泄漏定位，通过开展数值仿真，得到了泄漏工况下基于流体压力波的数据信息，通过小波变换方法可以较好地完成数据降噪与奇异点捕捉，基于波速完成泄漏点位置的估算。同时，借助具有动态记忆特性的反馈型Elman神经网络，开展了泄漏工况下的网络训练和预测。结果表明，该方法可适用于管道泄漏点的定位仿真，具有较好的准确率和可靠性。