蒸发式冷凝器的盘管截面形状对传热影响的数值模拟

李 闯，刘良旭，李海英，尹贻民，李富鹏

(华北理工大学冶金与能源学院，河北 唐山 063210)

在工业生产上，我国的能源消耗问题十分严重，生产同质同量的产品，会比国外多消耗几倍甚至更多的能源，造成极大的能源浪费；在我国，随着冷却水的应用越来越广泛,直接排放冷却水不仅会造成热污染，还会造成更大的经济和资源浪费，因此有必要重用这些冷却水循环来缓解目前的缺水状况[1]。

蒸发式冷却器其自身是一种改良的冷却设备，最早可见于凉水塔。对于其如何改进强化换热效率，一直都是国内外比较热门的话题[2]。蒸发冷却式冷凝器相比其他两种冷凝器具有许多优点，其中节水节能是其最大的优势，其次它还结构紧凑，占地面积小，而且维修起来相对比较容易，因此越来越受到国内外的广泛关注。Maria Fiorentino指出蒸发式冷凝器相对于空气冷却式冷凝装置在较低的冷凝温度下运行，与水冷却式冷凝器相比，耗水量减少[3]。Feifei Wang指出使用潜热的蒸发式冷凝器减少了水资源浪费，具有节能优势[4]。刘旭指出半圆形波纹板的水膜稳定时间较慢，传热面积较大，换热性能较好，而且不同板结构的蒸发式冷凝器具有不同的最佳喷淋量[5]。邵光明等人通过分析蒸发式冷凝器制冷系统的环境空气温度、相对湿度、湿度和焓，得到了蒸发式冷凝器制冷系统能耗的变化规律[6]。

通过以上分析可见，我国在对蒸发式冷凝器的研究上相当丰富，但缺乏实质性的模拟研究，而随着全世界资源的紧缺以及人类发展的需要，节水节能要求的不断深入，对蒸发式冷凝器的换热效率要求也越来越高。本文对相同材料的椭圆管和圆管两种不同的截面形状进行数值模拟，选定合适边界条件，得出两种不同截面下的换热情况。

1 数学模型

1.1 建立模型

为了简化计算，本模拟不考虑喷淋水的影响且以八排四列的换热管束为例来进行研究。蒸发式冷凝器的外形结构为长方体，常温下的空气从底部进入，被加热后的空气从上方排出。结构示意如图1所示：

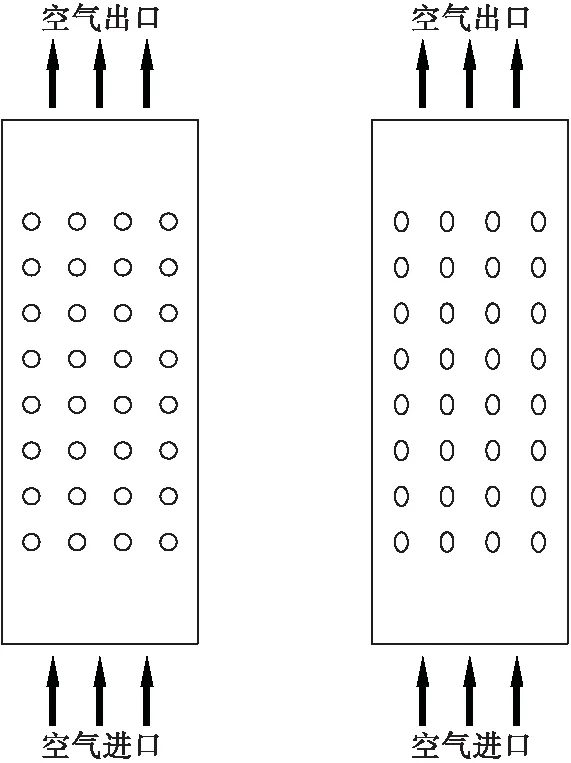
图1 圆管型和椭圆管型蒸发式冷凝器外形结构

其中，蒸发式冷凝器以及换热管束具体结构尺寸如表1所示。

表1 蒸发式冷凝器以及换热管束结构尺寸表 mm

两种形式在Fluent中的网格划分如图2所示：

图2 圆管型和椭圆管型在Fluent中的网格划分图

1.2 设定边界条件

考虑到模拟的局限性，做出如下简化假设：

(1)忽略重力作用；

(2)忽略浮升力的影响；

(3)空气流动均匀、不间断；

(4)流体流动采用无滑移速度边界；

(5)近壁面处选取为标准壁面函数处理。

下侧空气进口截面为速度进口velocity-inlet，空气温度为固定值300 K，空气流入速度为3 m/s。

上部为空气出口，设为自由出流outflow。

左右壁面设为wall，绝热Heat Flux为0；内部换热管束设置为wall-in，壁温恒定为363 K，管束材料为铜，管壁厚度忽略不计。

1.3 控制方程

根据蒸发式冷凝器的特点，本次模拟选用湍流模型。导热过程为非稳态导热，为方便计算，采取SIMPLE的算法。控制方程如下；

连续性方程：

(1)

能量守恒方程：

(2)

质量守恒方程：

(3)

动量守恒方程：

(4)

(5)

式中：u，v为流体速度,m/s；x，y为两个方向速度分量，m/s；ρ为模拟流体密度,kg/m3；T为模拟流体温度,K；U为模拟流体速度矢量,m/s；S为动量方程的广义源项,kg·m/s；μ为模拟流体动力黏度,N·s/m2；λ为模拟流体导热系数,,W/m·k；cP为模拟流体比热容,J/kg·k；ST为黏性耗散项,kg·m/s；

2 结果与讨论

2.1 模拟结果

本次模拟采用控制变量法，控制两种管型的截面周长相同，蒸发式冷凝器结构尺寸以及管间距均相同，进口风速均为3 m/s，进出口面积相同，管壁温均为363 K，改变管束截面形状，对圆管和椭圆管的模拟结果如下：

图3为进口风速3 m/s时，圆形和椭圆形不同截面形状的压力分布云图。由图3分析可知，在相同模拟条件下，椭圆管型空气进入时压力比圆管型要低大约0.32 Pa。同时椭圆管型压降分布更加均匀，因而有利于流体的稳定流动，可以更好地强化换热。

图4中可以看出，进口风速为3 m/s时，圆管型流体流动面涡流现象严重，管周围流体最低速度约低0.74 m/s，而椭圆管型则相对较好。因为在垂直于流体流动方向上，圆管截面比椭圆管截面大，导致阻碍流体流动，涡流现象明显。而椭圆管周围空气由于受阻碍作用较小，因此流速较快，有利于换热。

图3 进口风速3 m/s时圆管和椭圆管的压力变化云图

分析图5可以得出，进口风速为3 m/s时，两种管型在流场出口处的平均温度相接近，分别为305.88 K和305.64 K。图6为出口处的各个位置温度分布曲线图。对比之后发现，椭圆截面比圆形截面的高温分布更加集中管附近，更有利于换热。

2.2 计算结果

下面为圆管和椭圆管(椭圆率为1.5)的计算分析：

(1)两种换热管型的尺寸参数

椭圆管周长C为

(6)

椭圆管的截面面积f为

f=πab=π×0.015×0.01=4.7×10-4m2

(7)

图4 进口风速3 m/s时圆管和椭圆管的速度变化云图

椭圆管的当量直径di为

(8)

与椭圆管截面周长相同的圆管截面面积f0以及直径d0分别为

(9)

(10)

(2)圆管与椭圆管尺寸参数的比较

直径比：

(11)

截面面积比：

(12)

流速比：

(13)

雷诺数Rec比：

(14)

图5 进口风速3 m/s时圆管和椭圆管的温度变化云图

图6 圆管和椭圆管出口处的不同位置温度分布

努塞尔数Nuc比：

(15)

对流换热系数hc比：

(16)

通过比较分析可知，在截面周长相同的条件下，圆管管径相比椭圆管管径大了5.6%，截面面积大6%，而管内流体流速以及对流换热系数椭圆管却比圆管分别大12%和10%。即在材料相同的情况下，椭圆管截面面积更小，流体流速更高，对流换热系数更大，更有利于换热。

3 结 论

通过对椭圆管蒸发式冷凝器的截面形状对换热情况的理论分析，并建立数学模型，对比模拟结果与试验数据，得出以下结论：

(1)在相同模拟条件下，相比于圆管型椭圆管型空气进入时压力要低大约0.32 Pa。同时椭圆管型压降比圆管型更为均匀，因而有利于流体的稳定流动。

(2)圆管型流体流动面涡流现象严重，圆管周围流体比椭圆周围流体最低速度约低0.74 m/s，因而椭圆周围流速快，更有利于换热。

(3)两种管型在流场出口处的平均温度分别是305.88 K和305.64 K，但是椭圆管型的高温部分更加集中于管道周围，换热效果明显。

(4)在材料相同的情况下，管内流体流速以及对流换热系数椭圆管却比圆管要高2%，换热效果更明显。