概率论与模糊识别在塔里木河水资源承载能力评价中的应用

王立峰

( 阿克苏水文勘测局，新疆 阿克苏 843000 )

1 引 言

水资源是生态环境健康发展与经济社会运行、民生安全的必备基础资源，近几年来随着经济快速发展、城镇化加剧、人口增加，水资源需求量与日俱增，我国北方地区水资源短缺已成为限制区域可持续发展的重要因素[1-2]。水资源承载力是衡量一个地区在社会和生态系统平衡情况下能支撑的农业、工业等的最大限度[3]。众多国内外学者已经探索出了一系列的办法，那娜运用PSR模型对于辽宁省的水资源承载能力进行了评价，得出了较好的结果；张媛媛借助三维生态足迹模型对唐山市水资源承载能力进行了综合的评判，结果表明与实际情况相一致；张元杰结合了昌吉州最严格的水资源管理制度，巧妙的运用了投影寻踪技术对水资源承载能力进行了探索，但是现有的评价方法也存在着一些缺陷，对于指标体系的构建，目标权重的求解掺杂了人为因素以及客观因素而导致有误差[4-5]。

文章主要采用贝叶斯公式和模糊识别耦合，分析单个水资源承载力评价指标隶属于某个等级的概率[6]。接着用最大似然分类准则判定该指标等级，并引入组合赋权法与相对隶属度综合确定各指标的权重方法。最后将其应用到评价塔里木河水资源中去。

2 贝叶斯公式和模糊识别耦合模型

2.1 贝叶斯公式

O1，O2，…,On为组成一个完备群Ω，R为Ω中的任一事件，R能且只能与互不相容的O1，O2，…,On中的某一事件同时发生，若P(Oi)>0，(i=1,2,…,n),P(R)>0,则有

(1)

水资源承载力指标实测矩阵为X=(Xjk)mn，其中n表示水资源承载力评价样本个数；m表示指标项数；x表示水资源承载力评价指标[7-8]。令水资源承载力评价指标矩阵J=(yij)mc，其中c表示水资源承载力状态或分级数；y表示评价指标的标准值；j=1,2,…,m；k=1,2,…,n；i=1,2,…,c。设Oi为某个评价指标Xjk属于承载力级别i的事件，i=1,2,…,c；k=1,2,…,n。

水资源承载力由条件概率P(Oi/xjk)来表述,先验概率P(Oi)=1/c。用贝叶斯公式来表示：

(2)

2.2 模糊识别模型

文本中1级水资源承载力是非常弱，其评价指标i的标准值yi1对承载力程度的相对隶属度为sj1=0；c级承载力为优，其指标i的标准值yic对于承载力的相对隶属度sjc=1。则yji的相对隶属度sji可从(3)给出：

(3)

同理，可根据式(4)：

(4)

将指标值越高，承载力程度越高的实测值xjk转变为对应的相对隶属度rjk。

由(3)、(4)式将X、J矩阵转化为相应的相对隶属度矩阵R=(rjk)和S=(sji)。矩阵R表示所有指标对于“承载力程度”的相对隶属度。

当然，样本中指标对于承载力的影响程度有区别，文章中求权重采用了组合复权法，将主成分分析法和层次分析法结合起来，同时从主观和客观的角度对其进行计算，避免过大的误差，表示为：

(5)

主成分分析法计算出的权重为v′；层次分析法计算出权重为v″。用距离函数d(v′,v″)来表示两者的一致性程度：

(6)

用线性加权法计算v，公式如下：

v=αv′+βv″(7)

其中α、β分别表示主成分分析法和层次分析法的权重的分配系数。

距离函数和分配系数间关系到一致性程度，对本次计算有很大的影响，因此，令二者等同。同时避开正负号对结果的影响，取二者的平方来表示：

d(v′,v″)2=(α-β)2

(8)

α+β=1

(9)

用贝叶斯公式判别某一指标评价等级的计算步骤为：

(1)计算并判别各个指标xjk属某一等级Ai的概率P(Ai|xjk)=Pik

(10)

P(xjk|Ai)与Lik成反比关系。其中Lik为实测值xjk到标准值yik的绝对距离，计算式如下：

Lik=|xjk-yik|

(11)

(2)计算各个评价指标xjk的级别Bj

由最大似然分类的分类准则，取Pik中最大值作所属级别作为单个承载力评价指标xjk的评价级别Bj。

(3)计算各个指标的权重ωjk

构建的n个样本m项指标的权重矩阵A由超标权重和指标权重相乘而得：

(12)

将A中各权重值按列归一化：

(13)

(14)

W表示承载力评价综合权重矩阵，指标综合评价值见表1。

表1 评价因素等级表

3 实例应用

3.1 研究区域概况

塔里木河由发源于天山山脉的阿克苏河、发源于喀喇昆仑山的叶尔羌河以及和田河汇流而成。流域面积19.8万km2，最后流入台特马湖，塔里木河全长[12]f2137km，仅次于伏尔加河、锡尔—纳伦河、阿姆—喷赤—瓦赫什河和乌拉尔河，为世界第5大内流河，中国最长的内流河。位于新疆维吾尔自治区塔里木盆地北部。

按照行政区将塔里木河流域分成5个区域分别对其进行评价，但是该流域的水资源总量紧缺，水资源问题较为突出所以，对流域的水资源承载力进行评估，从而找到解决办法刻不容缓。

经过实地勘测与当地数据相结合，将5个区域的实测数据列于表2。

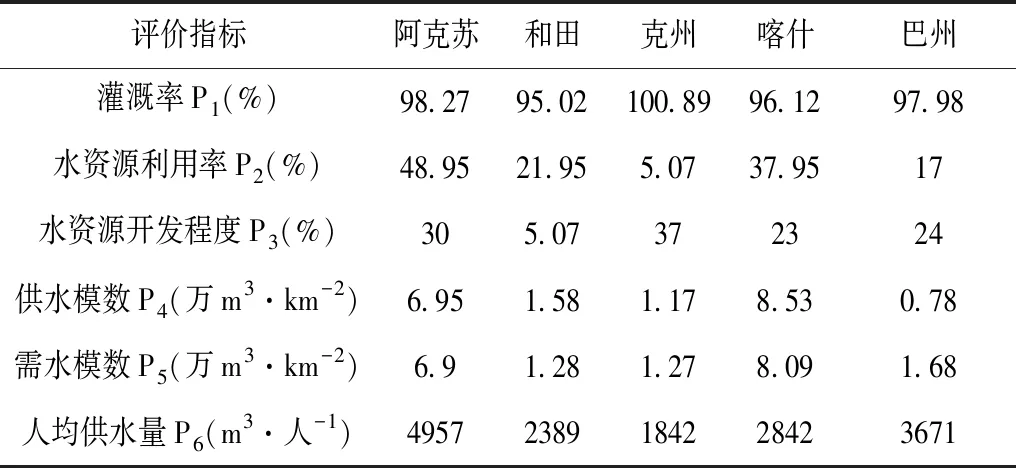
表2 评价实测值

3.2 模型求解

由表1、表2应用式(3)、(4)得：

参考文献[9]中对承载力评价指标间的权重计算法，求得各指标权向量为v=(0.215,0.306,0.198,0.089,0.187,0.007)[9]。

由式(12)计算得综合矩阵A，并按列归1一化得综合权重矩阵W：

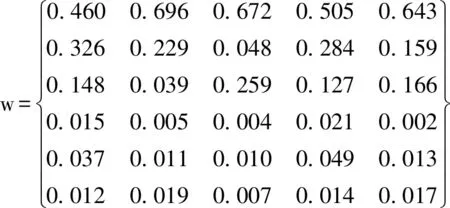
由式(10)、(11)计算得各指标xjk的评价等级矩阵Bj：

由矩阵W和Bj计算得脆弱性评价结果(评价级别)见表3：

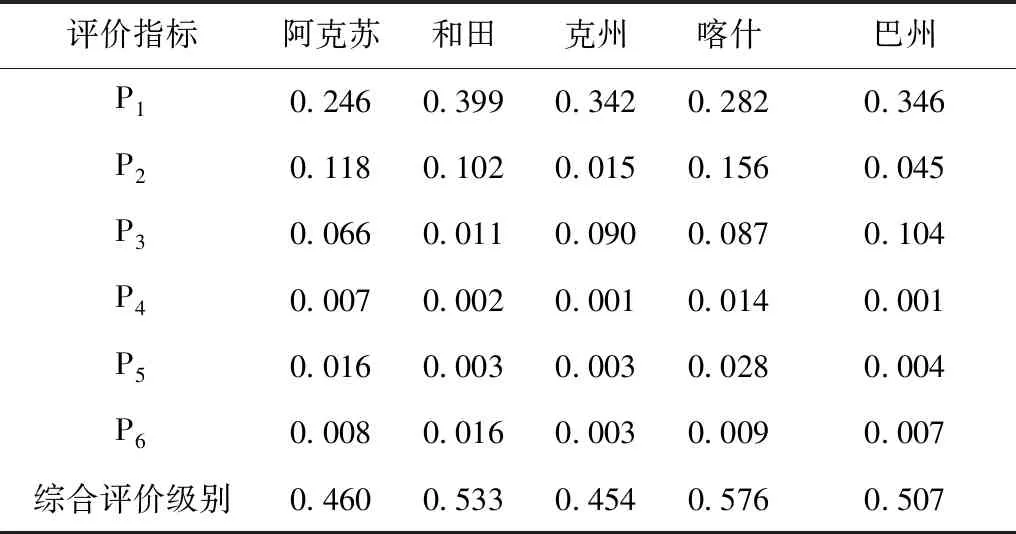
表3 承载评价结果

参考文献[10]中对水资源承载力的评判标准见表4[10]。

表4 水资源承载力评价表

表3的计算结果显示：5个区域水资源承载能力均为2级，水资源总体来说较好，但是仍然存在一系列问题，比如供给方面和水质方面，故而仍需加大对该地的水资源的管理与监控。

4 结 论

1)水资源承载力的指标个数和种类的选取具有不确定性，各个等级之间和每个等级本身对评价目标也具有不确定性。

2)文章根据各个区域指标的多个不确定信息，采用贝叶斯公式的不确定性方法进行水资源承载力评价。

3)文章在组合赋权法的基础上加入相对隶属度的概念，结合指标间和指标内部的相对隶属度对目标的影响确定权重。应用实例表明，评价结果更加准确、贴近实际。