求解第一类越补参数的简化算法
2020-05-07王志云
王志云
(黑龙江省齐齐哈尔市水利工程建设质量与安全监督站,黑龙江 齐齐哈尔 161005)
由于弱透水层是由粒径比较细的黏土或粉砂组成,在某些情况下,从其储存量中释放出来的水量比承压含水层储存量中释放出来的水量还要多[1],因此,研究具有越流补给条件下的水文地质参数的求解具有重要意义。到目前为止,求解第一类越流补给条件下水文地质参数的方法已有较多研究成果[2-7],这些研究成果均是针对定流量非稳定流或稳定流抽水试验条件下获得的,但在许多情况下,受外部条件限制,在抽水井影响范围内无适合作为观测孔的管井,或虽有井孔因一直处于取水状态或其他缘由无法作为观测孔使用。因此,研究第一类越流补给非稳定流条件下定降深抽水试验推求水文地质参数的方法同样具有实际意义。
目前,利用定降深抽水试验推求第一类越流补给非稳定流条件下水文地质参数的方法主要为标准曲线比对法[8],由于标准曲线比对法靠人工手动拟合,实际工作不但受图表束缚,而且求解成果因受标准曲线的密度及比对过程人为因素的影响,求解成果的精度难免存在误差[9]。因此,提出一种更加简单适用的利用定降深抽水试验推求第一类越流补给非稳定流条件下水文地质参数的计算方法十分必要。
1 公式的建立
1.1 基本计算公式
在抽水影响范围内,如含水层为多层、各层近似水平、均质等厚、各向同性并侧向无限延伸,且有上覆或下伏的弱透水层在越流含水层抽水时能产生越流补给,此时的地下水渗流运动即为第一类越流补给。其定降深越流系统井流问题的基本求解方程为:
(1)
解此问题得到如下井流流量方程为:
(2)
其中:
(3)
(4)
(5)
(6)
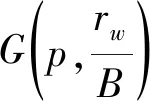
1.2 简化公式的建立
根据抽水井定降深的观测资料完成Q~t经验曲线绘制,并通Q~t曲线修正个别点的实测误差。在修正后的Q~t曲线上选取A、B、C三点,对应的坐标值分别为(tA,QA)、(tB,QB)及(tC,QC),将其分别代入式(2)可得到以下方程组:
(7)
(8)
(9)

(10)
(11)
式中:QA(tA)、QB(tB)及QC(tC)分别为与抽水历时tA、tB及tC相对应的抽水流量;m3/d。
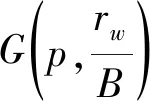
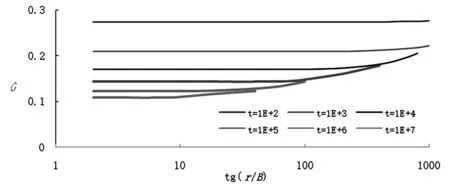
图1 G-r/B-t关系曲线
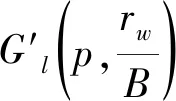
经反复优化拟合比选,逐次逼近即可获得第一类越补系统定降深井流流量函数式(3)的最优替代函数为:
(12)
其中:
(13)
Bl=-0.437652-9.402317×10-5p0.8134
(14)
(15)

将函数式(12)替代式(3)并分别代入式(10)、(11),经进一步整理即可获得以下求解方程:
(16)
(17)
由式(16)、(17)可得:
(18)
其中:
AAB=AA-AB,ABC=AB-AC
(19)
BAB=BA-BB,BBC=BB-BC
(20)
CAB=CA-CB,CBC=CB-CC
(21)
式中:AAB、ABC、BAB、BBC、CAB、CBC均为与α、tA、tB(或tB、tC)有关的中间变量。
根据已知的tA、tB(或tB、tC)通过假设不同的α即可利用式(13)-(15)及式(19)-(21)分别求得相应的中间变量,代入式(18)即可分别求得等式左、右两侧的数值,如等式两侧数值相等,则所设α即为求解值,否则,重设α值,直至式(18)左、右两侧的数值相等。为加快求解α的计算过程,α的初设值可在104-107m2/d之间选取[12],并采用黄金分割法(即0.618法)通过逐次逼近完成具体求解计算[13]。
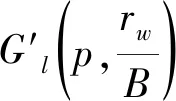
(22)
再由式(23)求得越流含水层的弹性释水系数S为:
(23)
由式(24)求得越流层的渗透系数为:
(24)
2 精度比较及验证
2.1 精度比较

(25)
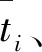

图2 式(12)拟合式(3)误差包络线

2.2 结果验证
2.2.1 算例
以某地水源井抽水试验为例,已知该井孔位于冲积平原上,rw=0.15m。越补层为承压水砂砾石含水层,厚度M=23m。该层上为亚砂土夹少量砾石之弱透水层,厚度M′=22m。在这两层之上、下部分别为潜水含水层及红黏土隔水层。抽水时,承压含水层得到弱透水层中地下水的渗流补给。试验井的出水量用阀门压缩控制,用安装在出水口的流量计读取水泵单位时间的抽取水量。已知开泵0.5 h后,当水泵出水量为120 m3/h时,井中的水位降深为 m,利用阀门压缩水泵出水量,控制该降水深度为定值,分别读取不同抽水历时t所对应的水泵出水流量Q,有关试验数据见表1。试计算越流含水层的水文地质参数。

表1 某水源井降深抽水试验观测数据
根据表2绘制Q~t关系曲线(见图3),在Q~t关系曲线上选取:tA=60min,QA=115.64m3/h;t”B=150min,QB=109.67m3/h;tC=300min,QC=106.84m3/h。

图3 Q~t关系曲线
根据α的值域范围,初选α=1×105,由式(13)-(15)及(19)-(21)可分别求得:AAB=-17692.17166,BAB=2.00489,CAB=0.01312,ABC=-28832.01079,BBC=2.88992,CBC=0.02118,则:
式(18)的左端为:
式(18)的右端为:
式(18)的左端与右端之差为0.637。
再设α=5×105,采用与上述相同的计算方法可求得式(18)的左端为88.968,右端为107.093,左端与右端之为-18.125。

2.2.2 曲线拟合验证
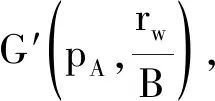

图4 Q-t关系曲线
由图4可见,采用文章所求参数及井函数替代式获得的曲线与实测各点非常吻合,证明文章的简化计算法具有较好的精度及适用性。
3 结 语
1)在工程适用参数范围内,文章提出的计算公式形式简单、求解过程直观简捷,不受图表束缚,避免了图表取值的人为误差,便于实际推广应用。
2)为有效提高计算成果的精度,考虑流量观测成果可能存在误差,在利用文章方法计算前,可根据t、Q的观测成果完成Q-t曲线绘制,并通过曲线修正相关流量Q值。
3)利用Q-t曲线进行(tA,QA)、(tB,QB)及(tC,QC)3个点选取时,为使各点具有更好的代表性,应尽量在Q-t曲线上按流量变化情况均匀选取。
4)采用与文章类似的方法也可完成类似水文地质参数的简化求解计算问题,文章不详述。
