红外成像制导半实物仿真安装误差分析与修正

孙志朋，赵世明，孙致月

（中国人民解放军91336部队，河北 秦皇岛 066000）

0 引言

随着精确制导技术的迅猛发展，红外成像制导技术的研究在军事领域得到广泛重视，该技术在各种对地对空对海制导武器中得到大量应用[1-3]。红外成像制导技术是获取目标和背景辐射的红外能量进行成像，通过处理得到目标空间信息完成目标的识别跟踪，是集光、机、电和信息技术于一体的综合技术，能够获取较多目标特征信息，具有非常高的制导精度[4]。

红外成像制导半实物仿真的工作原理是用系统的关键实物部件取代仿真系统中相应部分的数学模型，并连接到计算机仿真回路中进行试验，可以更加真实客观地反映系统在运行中的实际情况，提高了仿真结果的置信度[5-6]。红外成像半实物仿真在红外成像制导导弹导引头的研制和性能指标验证中起着非常重要的作用，较大程度地降低武器系统在研制过程中的成本和研制周期、提高效费比[3]。

在红外制导导引头半实物仿真试验过程中，由于导引头和红外目标模拟器都要架设在转台上，很难保证导引头光轴和红外目标模拟器光轴完全重合，从而不可避免会引入安装误差。这个误差会直接影响仿真过程中导弹的跟踪精度和脱靶量，对仿真结果的置信度产生一定影响[6-8]。本文通过反复试验测试分析出误差产生的规律，然后采用图像处理和数学分析建立误差模型，从而判断出误差产生的原因，再针对误差进行修正，避免了因误差对整个试验结果的负面影响。因此，对安装误差进行分析和修正对整个仿真实验具有重要意义。

1 误差分析建模

1.1 误差产生

红外成像半实物仿真系统由五轴转台、仿真计算机、控制系统和实时通讯网络组成。其中五轴转台的三轴框架上架设红外导引头，用于模拟导弹飞行过程中的姿态运动；两轴框架上架设红外目标模拟器[9-10]，与三轴框架随动，为导引头提供动态红外场景，如图1所示。

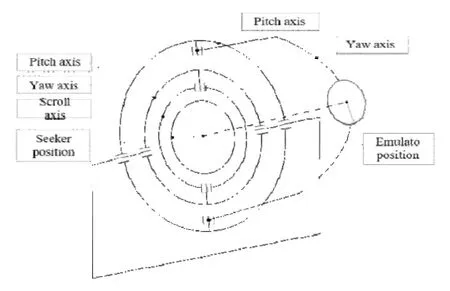
图1 五轴转台示意图Fig.1 The schematicdiagram of five-a xisturntable

导引头和目标模拟器需要使用夹具架设在转台上，因夹具在设计制造中会有一定的尺寸公差[11-12]，并且五轴转台、导引头和目标模拟器虽是高精度产品但仍有一定的误差量，导引头和模拟器由于各安装面的形位配合公差在安装架设后其光轴之间会产生偏差[11]，这些偏差包括位置偏差和角度偏差，如图2和图3所示，最直观的结果是导引头的显示窗口中心和模拟器的像元中心不重合，从而产生制导误差量。一般红外成像导引头的视场角为1°～3°，探测元数达到512×512及以上，所以这些安装误差的存在可能导致数个像素的差量，对制导的结果存在一定的影响，而且安装误差是客观存在不能消除的，所以就需要对其进行建模分析，对制导信息进行修正。

1.2 误差影响

因为安装误差，导引头光轴和目标模拟器光轴不重合，这就使得导弹在进入末制导段开始就有制导量的误差，一直到最后时刻存在。而且对导弹的制导精度和飞行轨迹都有一定影响。如图4所示，导弹M和目标T，在没有制导误差的情况，飞行轨迹为M-T，假设因安装误差引起的制导误差角度为φ，则导弹的飞行角度变为M-A-B-C-D，同时导弹落点由M点变为D点，产生一定的制导误差量。

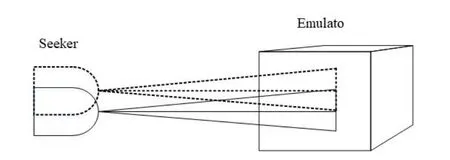
图2 位置偏差引起的误差图Fig.2 Error caused by position deviation

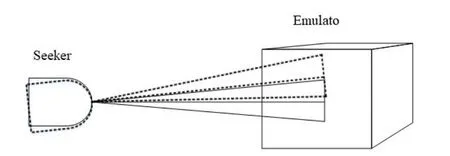
图3 角度偏差引起的误差图Fig.3 Error caused by angular deviation

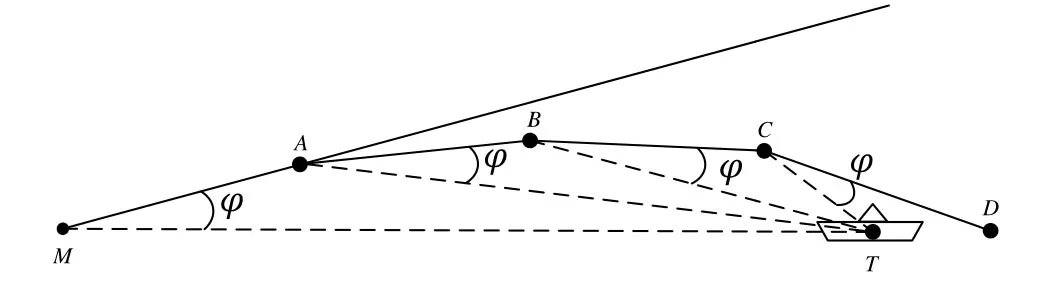
图4 误差对导弹制导结果的影响Fig.4 Error of missile guidance results

1.3 误差模型建立

安装误差存在3种情况：一是导引头存在安装误差，目标模拟器没有安装误差；二是导引头没有安装误差，目标模拟器存在安装误差；三是导引头和目标模拟器均存在安装误差。对于这3种情况，当转动五轴转台的滚转轴框使导引头发生滚动姿态变化，其他轴框不动处于零位时，在导引头控制机上的跟踪界面中目标模拟器的像元中心的运动轨迹是不同的。

建立坐标系如图5所示，基础坐标系XOY，坐标平面垂直于三轴框架的滚转轴，坐标原点为滚转框的回转中心，按导引头侦测方向看，水平向右为X轴正向，竖直向上为Y轴正向，为静坐标系；导引头测量坐标系XsOsYs，以导引头成像中心为原点（导引头光轴上），以成像图像为基准，横向向右为横轴Xs，竖向向上为纵轴Ys，为动坐标系。

在进行半实物仿真时，目标的测量值是基于导引头测量坐标系观测的，当导引头进行滚转运动时，模拟器图像的像元中心在导引头测量坐标系的位置也会发生相应变。设模拟器像元中心坐标为M(xm,ym)，导引头成像中心坐标Os(xOs,yOs)，初始值为Os(xOs,yOs)＝(rcosθ0,rsinθ0)，其中r=OOs，θ0为初始状态下OOS与OX的夹角，逆时针为正。通过坐标转换如下式：

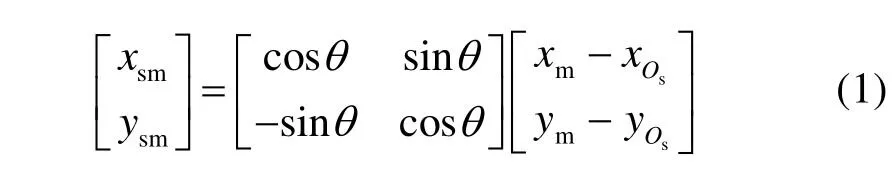
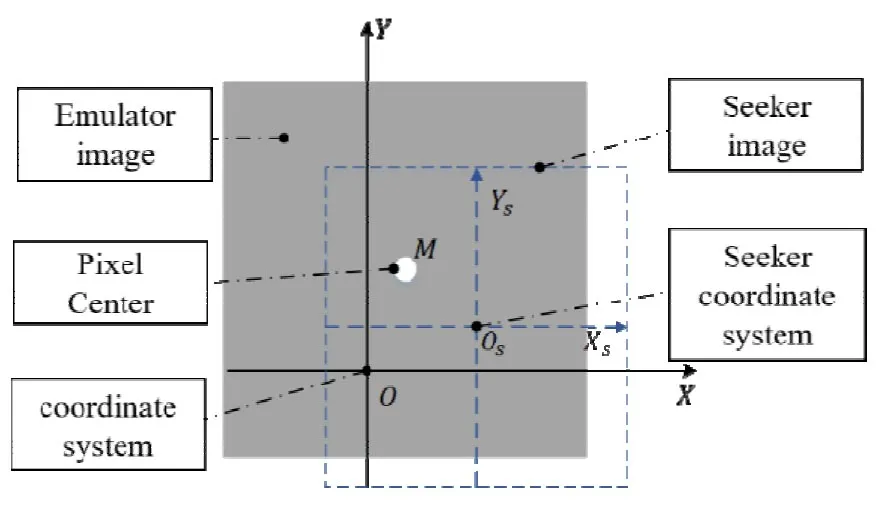
图5 坐标系关系图Fig.5 Coordinatesystem diagram

当导引头滚动θ角时，导引头成像中心坐标为Os＝(rcos(θ0＋θ),rsin(θ0＋θ))，则模拟器像元中心在导引头测量坐标系位置坐标为：

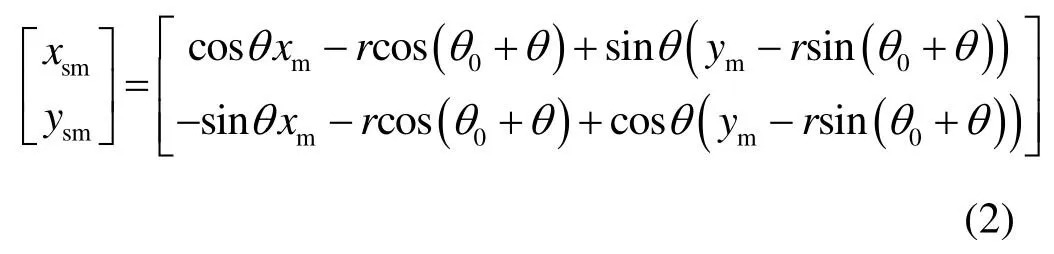
求得的位置坐标：

用(xOs0,yOs0)代替(rcosθ0,rsinθ0)得：

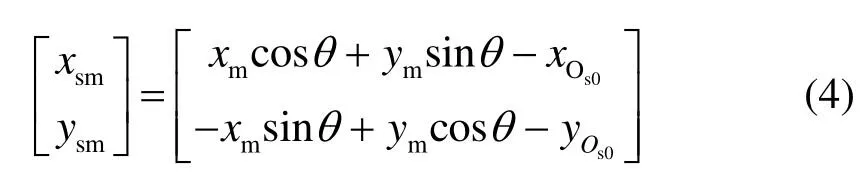
对导引头安装误差做如下讨论：

1）当导引头存在安装误差，目标模拟器没有安装误差时，此时M(xm,ym)＝(0,0)，将其代入式(4)得：

从式(5)可以看出随着导引头滚动模拟器像元中心运动轨迹是一个固定点。

2）当导引头没有安装误差，目标模拟器存在安装误差时，此时Os(rcosθ0,rsinθ0)＝(0,0)，将其代入式(4)得：

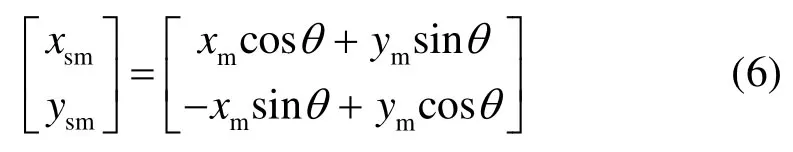
从式(6)可以看出随着导引头滚动模拟器像元中心运动轨迹是一个圆心在坐标原点半径为的圆。

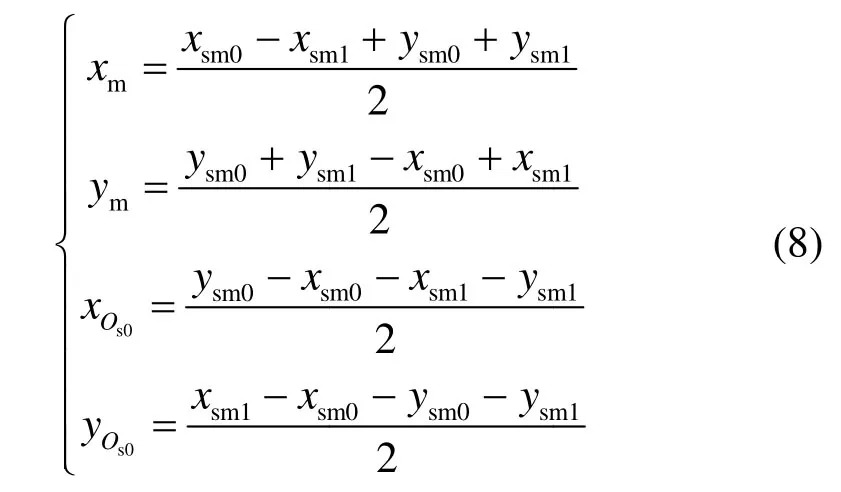
3）当导引头和目标模拟器均存在安装误差时，随着导引头滚动模拟器像元中心坐标如式(4)所示，其运动轨迹是原点为半径为的圆。

2 误差量解算

通过转动导引头在测得两个不同转动角度下目标模拟器像元中心在导引头测量坐标系下的坐标值的情况下代入式(2)就可对导引头和模拟器的误差量进行求解。假设初始状态下模拟器像元中心在导引头测量坐标系下的坐标值Ms0(xsm0,ysm0)，在导引头转动90°（视滚转框的旋转范围选取）的情况下模拟器像元中心的坐标值Ms1(xsm1,ysm1)，代入式(4)得到联立方程：

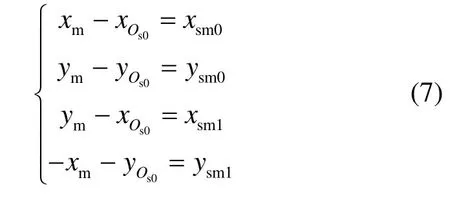
对方程(7)进行求解得到导引头和目标模拟器安装误差的数学模型：

式(8)即是基础坐标系下初始状态的导引头成像中心坐标Os(xOs,yOs)和目标模拟器像元中心坐标M(xm,ym)，即安装误差量。

从数学模型可以看出，安装误差求解关键是获得导引头测量坐标系中导引头两个不同滚动姿态下的模拟器图像像元中心的坐标Ms0(xsm0,ysm0)和Ms1(xsm1,ysm1)，而此信息很难在导引头的输出接口数据中获取。但是可以通过对导引头输出的探测图像进行图像处理获得像元中心坐标像素。OpenCV由许多模块组合而成，包含了许多计算机图像的数学运算处理功能[13-14]，可以通过OpenCV来实现导引头探测图像的处理过程。

设置模拟器使其成像的图像如图6所示，白点为图像的中心，按固定速度转动导引头，录制θ角由0～2π导引头探测图像的视频，对导引头旋转一个周期内视频进行处理，其中某一帧图像进行目标检测[15]获得像元中心的形心坐标，处理结果如图7所示。

图6 目标模拟器成像图像Fig.6 Target simulator image

图7 导引头目标处理检测结果Fig.7 Seeker target processingdetection results

在程序中将每一帧图像处理后的坐标值输出到TXT文本，然后用Matlab调用进行画图如图8所示，根据图像对照公式(3)～(5)就可以判断出是哪种误差情况。选取θ＝0°和θ＝90°下的坐标值代入式(8)，便可以求出导引头和目标模拟器的安装误差。

3 误差补偿

对误差的补偿本文主要提出两种思路：一是根据求解的误差量，转动转台相应的轴框，使模拟器像元中心和导引头成像中心重合，修改转台控制程序，将此状态下的各轴的位置修正为零位。这种方法可以适用于飞行过程中滚动姿态变化很小的弹（如巡航弹），滚动姿态变化大的弹则不适用，另外修改控制程序需要制作转台的专业人员进行，存在客观的局限性，且反复修正不利于转台的技术状态稳定。

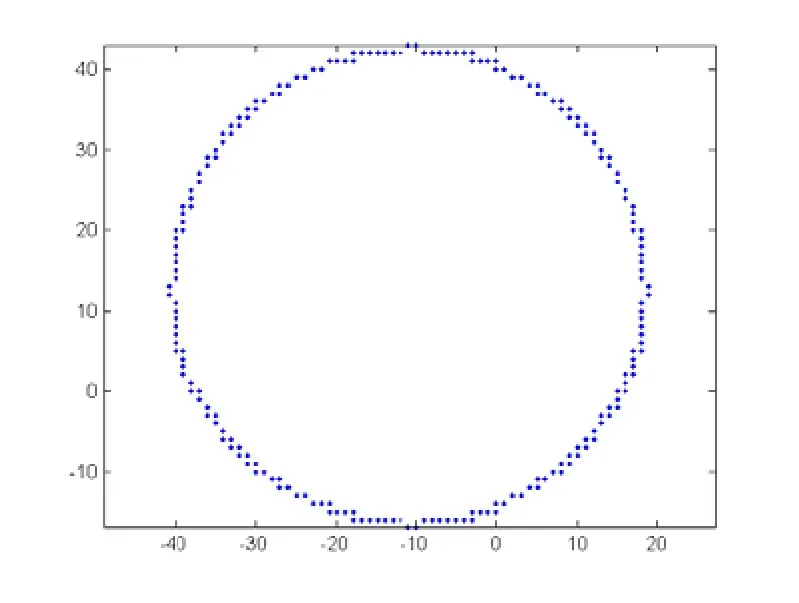
图8 模拟器像元中心的运动轨迹 Fig.8 Motion traceof thesimulator imagecenter

二是将求解的误差量及不同滚动的角度加载到导引头输出接口的制导量中，在模型中添加补偿量φx、φy，以达到对整个制导弹道进行修正。

φx、φy的求解公式为：

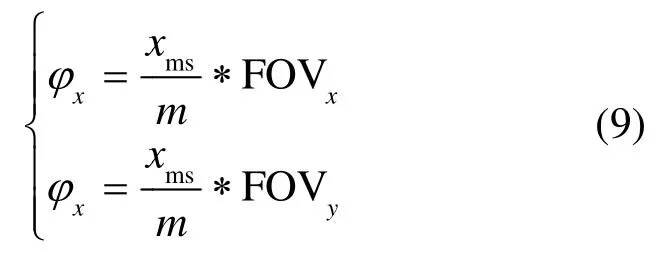
式中：(xms,yms)为弹体某滚动角度下导引头观测坐标系下的模拟器像元中心的坐标；m、n导引头像元数；FOV为导引头的视场角。这种方法是在导引头输出制导量中加入了补偿模型，可实现对导引头制导信息的修正，对硬件的稳定性影响不大，其缺点是只是数学模型上的修正，导引头和模拟器的光轴位置关系没有变化，也就是模拟器成像中心和导引头观测窗口中心依然没有重合问题依旧存在，但从误差修正前后脱靶量的对照中可以看出制导精度有所提高。

采用第2种方法进行修正后对脱靶量的影响如图9所示，图中坐标分别是脱靶量在x向和z向的分量。

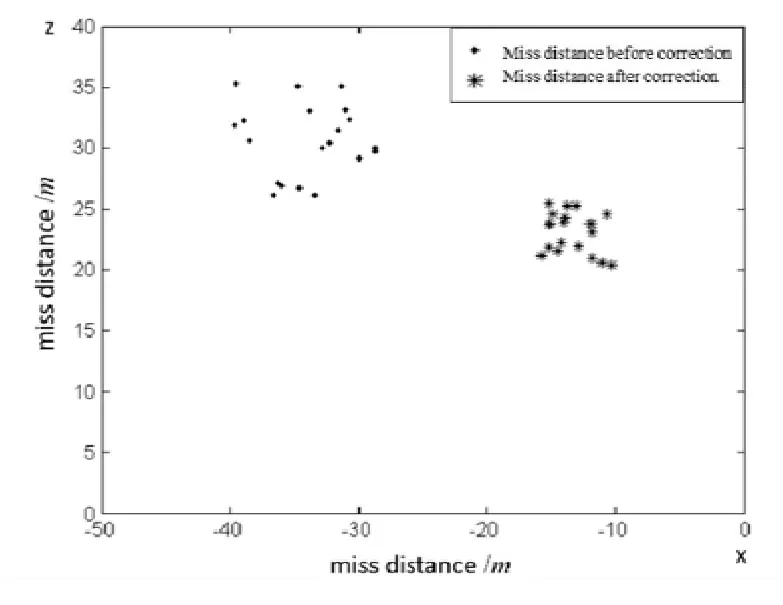
图9 修正前后脱靶量统计图Fig.9 Statistics of missed amount beforeand after correction

4 结论

通过对红外制导半实物仿真中出现的误差进行了产生的原因分析，并建立了误差的数学模型及判断3种安装误差的方法，并进行推导得到了计算导引头和目标模拟器安装误差的公式，然后应用OpenCV图像处理工具对导引头图像进行处理得到误差量并提出了误差补偿方法，最后将误差量代入弹道模型进行验证，通过对实验前后脱靶量的统计对比表明此误差修正对仿真中提高制导精度有一定的优化作用。