基于小波-Contourlet变换的偏振图像融合算法

沈薛晨，刘 钧，高 明

（西安工业大学 光电工程学院，陕西 西安 710021）

0 引言

偏振成像相对于传统成像技术，其成像效果进一步提高，偏振成像技术利用物质材料间不同的偏振特性来探测目标，提高了复杂背景下目标的识别率。又因为偏振特性图像能更加准确地描述目标特征，故而将偏振特性图像进行融合，将相互区别并互补的信息融合在一起。因此，偏振图像融合成为图像融合领域的研究热点之一[1-2]。

融合后的偏振图像场景信息更加丰富，融合了各源图像独有的图像信息。关于偏振图像的融合研究，不少学者做了许多研究，例如，申慧彦等[3]利用小波变换，对偏振图像进行融合；在红外偏振方面，陈伟力[4]等人，以及虞文俊、顾国华[5]等人，皆采用与小波变换相关的融合变换方法；张肃等人[6]提出了一种基于小波提升算法的偏振信息融合方法，能够提高目标识别率；蔡怀宇等人[7]通过偏振融合，增强了人脸轮廓信息；朱达荣等[8]提出了一种基于非采样剪切波偏振图像融合方法提高图像质量。

这些融合图像取得了不错的效果，改善了图像质量，但却尚有提升的空间，为进一步提高图像的融合效果，本文在小波-Contourlet变换[9]的基础上，提出了区域特性能量与主成分分析（principal component analysis, PCA）变换相结合的融合规则，采用PCA变换对低频进行融合，不仅可以提取各源图像中的重要成分，还具有较好的去干扰性；高频部分，采用区域特性能量，最大限度地保留每个源图像的细节信息，融合后的图像不仅在主观视觉上拥有良好的观察效果，而且通过客观评价函数的数据表明，细节纹理和场景信息保留较为充分。

1 图像预处理

图像融合是针对各源图像的对应像素进行信息融合处理，所以图像的精度和质量在很大程度上决定了图像融合的效果。为了减小像素位置差异和噪声污染带来的影响，需提前对图像进行去噪增强和配准[1]。

通过实验获得的4幅角度偏振图像，噪声较小，在此基础上，进一步提高实验精度，运用中值滤波进行去噪处理。以偏振角度为0°的图像为参考图像，采用SURF角点检测算法，对其他3幅角度图像（45°,90°,135°）进行配准；利用随机采样一致（RANdom sample consensus, RANSAC）方法提高配准精度。最后，得到一组新的低噪声、配准度较高的不同角度的偏振图像。

2 偏振特性图像的获取

偏振信息常用Stokes矢量(I,Q,U,V)T描述，其形式为(S0、S1、S2、S3)来表示，Iθ为该角度下光的强度[10]，其定义式表示如下：

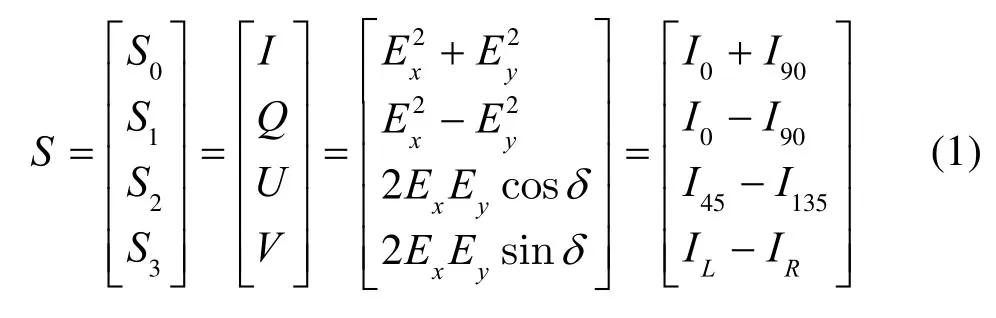
利用上式可推导得到3幅偏振特性图像：偏振强度图像I(S0)、偏振度图像（degree of polarization, DoP）和偏振角图像（angle of polarization, AoP）。由于偏振角图像AoP清晰度较低，将降低融合效果，故而只融合强度图像I与偏振度图像DoP。

在确定0°参考方向之后，任意一个偏振方向θ上的透过光强为：

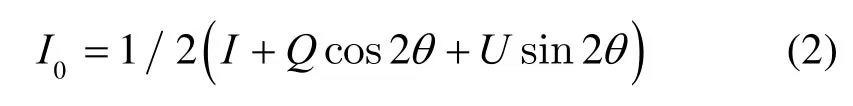
通过上式可得到偏振强度图像I(S0)。其次，结合Stokes矢量的I、Q、U三参量[11]，再根据下式(3)可计算出偏振度图像和偏振角图像：

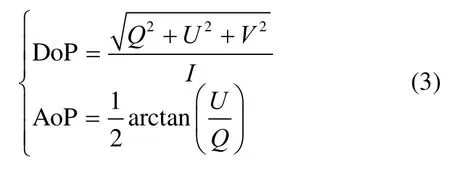
又因圆偏振的及其稀少，通常默认为0，此时转化成线偏振度（degree of linear polarization, DoLP）：

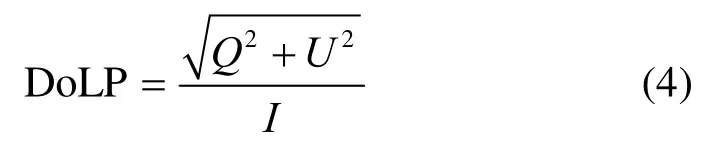
将预处理后的4幅偏振角度图像（图1所示），经上述理论公式计算后，可得出图2所示的偏振强度图像I(S0)和线偏振度图像。

3 小波-Contourlet融合方法

小波-Contourlet变换（wavelet-based Contourlet transform, WBCT），是在Contourlet变换基础之上，将小波变换与Contourlet变换相结合的一个改进[12]，是一种有效且快速的图像融合变换方法[13]。图3为Contourlet变换流程框架图。

WBCT由两级滤波器组成。第一级，WBCT用小波变换进行多尺度分解，每一层小波会获得4个系数：一个低频系数（LL），3个高频子带（LH、HL、HH），如图4中间部分所示，每一层分解成4部分，即4个系数。第二级是方向滤波分解，对3个

图1 预处理后4幅偏振角度图像Fig.1 Four polarization angle images after preprocessed

图2 偏振强度图像和偏振度图像Fig.2 Polarization intensity image and polarization degree image

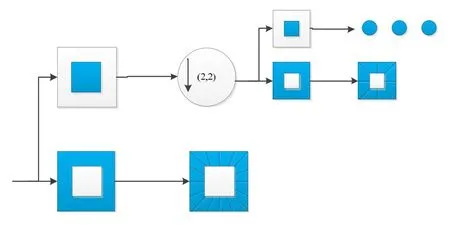
图3 Contourlet变换框架图 Fig.3 Contourlet transform frame diagram

高频子带使用方向数相同的方向滤波器组[14]，如图5所示，最后剩余一个低频系数未进行方向分解。其中，4组频率-方向分层系数可由下式表达[15]：

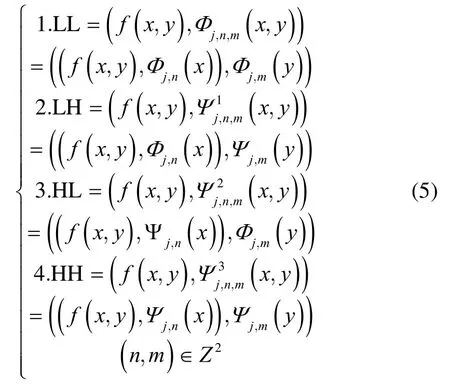
式中：Φj(T)表示T方向上的尺度函数投影；Ψj(T)表示T方向上的小波函数投影。利用小波-Contourlet变换，将偏振强度图像和偏振度图像进行分解，得到2个相对应的低频系数，以及若干个互相对应的高频系数。

4 偏振图像的融合

4.1 融合步骤

本文融合算法的总体思路为：

首先，将预处理后得到的新的4幅不同角度偏振图像进行偏振计算，通过Stokes矢量法获得DoLP和AoP图像。

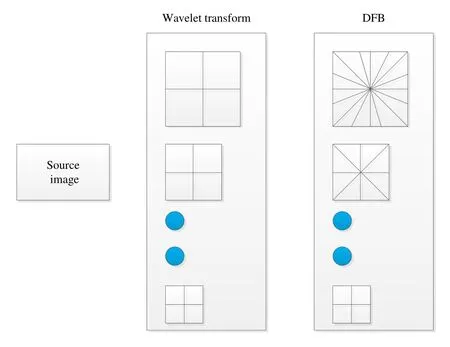
图4 WBCT的框架图Fig.4 The frame diagram of WBCT

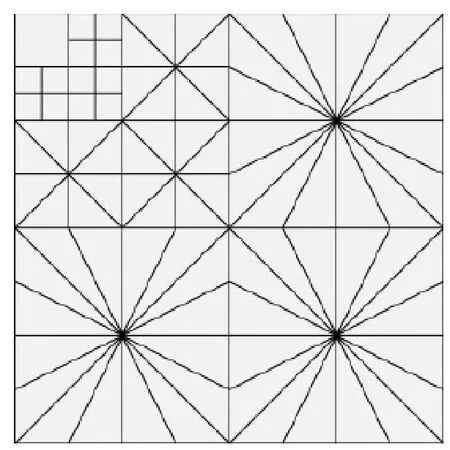
图5 WBCT变换示例图 Fig.5 Sample diagram of WBCT transformation

其次，将得到的强度图像I和线偏振度图像DoLP进行分解；分解得到的2个低频系数基于PCA变换融合，高频系数一一对应，基于区域特性能量进行融合。

最后，将融合后的高频系数和低频系数，进行小波-Contourlet逆变化，得到最终图像。流程示意图如图6所示。

4.2 融合规则的选取

融合规则的选取，是图像融合过程中的重要部分，它直接决定了融合图像质量的优劣。融合规则的要求如下：以保留源图像中的重要信息为主，尽可能将相互区别并互补的信息兼容融合，无用信息尽可能地避免融入。同时，算法必须具有可靠性、稳健性。

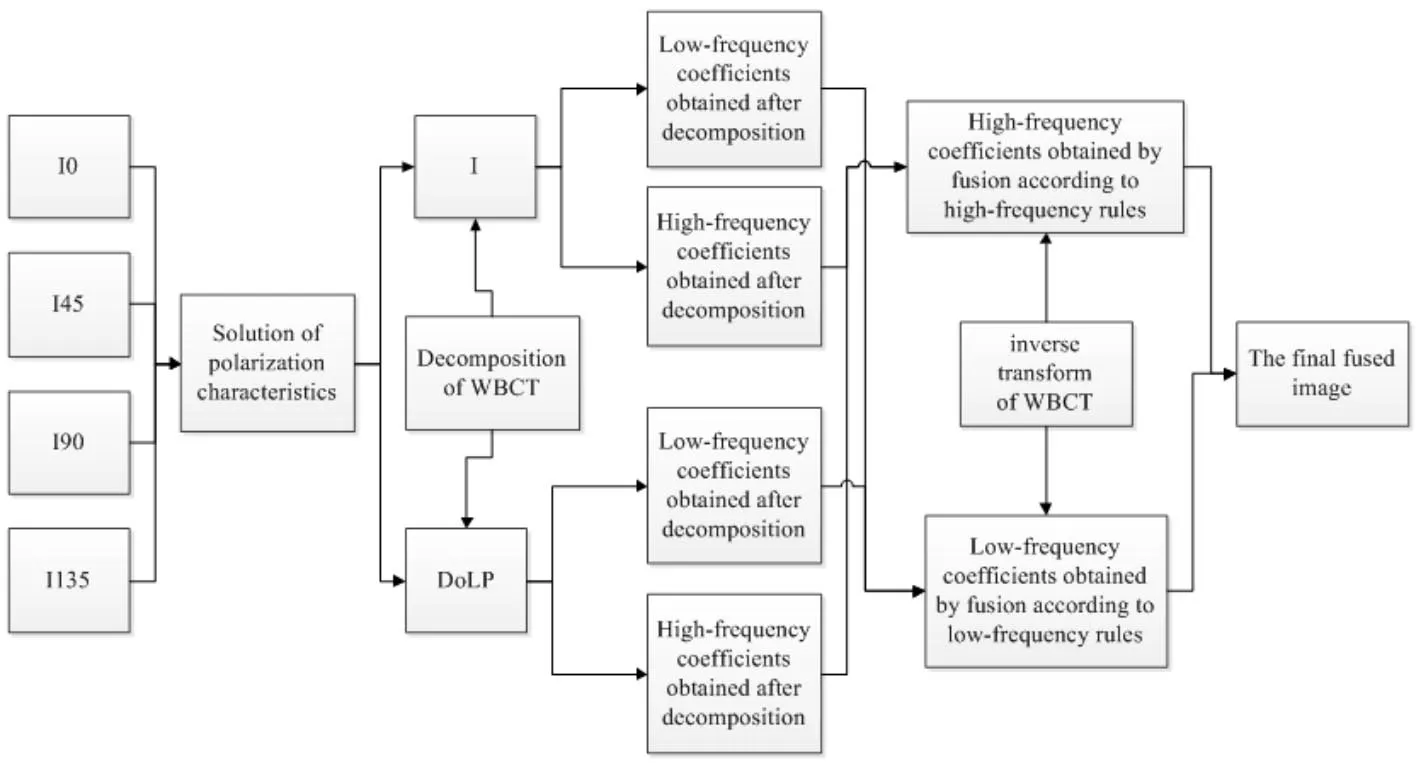
图6 流程框架图Fig.6 Flow chart of image fusion

4.2.1 低频融合规则的选取

低频融合规则：低频信息代表着图像中的主要成分，即除去图像中灰度或亮度变化剧烈的部分外，剩余部分为低频信息，描述了图像的整体综合强度。本文通过PCA主成分分析融合低频信息。

经过PCA变换之后，低频信息中最重要的信息占比最大，成为融合的第一成分，其余冗余信息依照占比，分别依次处理，去除冗余，突出图像的重要信息[16]。

设LA和LB分别为源图像A和B的低频信息，(a,b)T为LA和LB经过PCA变换所得的特征量，则权重WA和WB分别为：

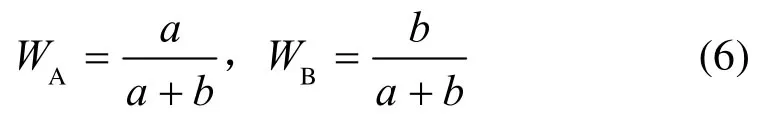
融合后的低频信息为：

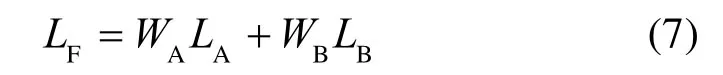
4.2.2 高频融合规则的选取

高频融合规则：高频信息代表了图像的细节纹理和边缘轮廓场景等部分，是人眼对图像最为关注的区域，反映了图像中亮度或灰度值变化剧烈的成分。

由于图像中像素与其邻域间的像素，相关联系程度比较大，所以采用区域特性能量的方法进行高频融合。

取中心像素及其邻近区域的能量作为融合标准。将某像素点(x,y)的w区域(x－k,y－k;x＋k,y＋k)能量定义为其邻域窗口内的能量，公式如下：

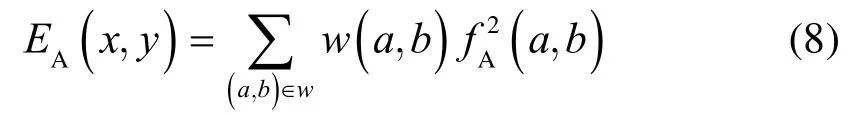
式中：x－k≤a≤x＋k，y－k≤b≤y＋k，窗口上下左右宽度皆为w(w=2k＋1)个像素，W(a,b)为权值，离像素点(x,y)越远则权值越小，f(a,b)为(a,b)处灰度的数值。定义匹配度RAB(x,y)如下：

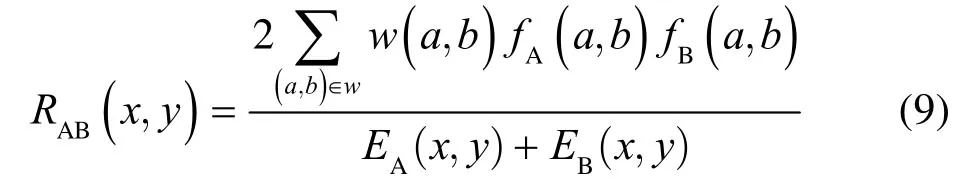
其值在0和1之间变化，接近0就说明两区域的能量差别就大；接近1，说明差别较小。最终可归纳为以下公式：

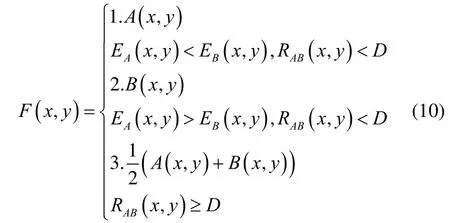
式中：D为能量匹配度阈值[17]。

首先计算两幅图像的匹配度值，若匹配值接近设定的阈值，或匹配值超出阈值，如上式中的最后所示，说明两幅图像对应的邻近区域能量值差异较小，采用加权平均的融合方法；若阈值远大于匹配值，说明两幅图像对应的邻近区域能量值差异较大，如上式前两者所示选取邻近区域能量最大的高频系数作为融合图像的高频系数[18]。

5 实验结果与分析

取偏振强度图像I和偏振度图像DoLP进行融合实验，图像大小为1024×1024，WBCT采用的小波分解为3级，DFB方向为16-8-8，小波变换采用的是9-7小波。CT采用的LP分解为3级，DFB方向为16-8-8，金字塔变换采用的是LP变换。在高频和低频都采用区域特性能量融合规则的基础上，将WBCT与拉普拉斯金字塔变换、PCA、小波变换这几种方法进行比较，如图7所示。

采用信息熵（entropy, E）、平均梯度（average gradient, AG）、边缘强度（edge strength, ES）和交叉熵（cross entropy, CE）等客观评价函数对融合效果进行定量评价。评价指标数据如表1所示。

另外，由于WBCT是在CT的基础上发展而来的，为了验证此算法的有效性，也为了验证本文融合规则的有效性，在之前拟定的设定基础上，选用更多的融合规则，对WBCT和CT进行对比。采用的融合规则依次为：高频和低频都采用区域特性能量融合规则；低频采用区域特性能量融合规则，高频采用像素取绝对值最大；低频采用PCA融合规则，高频采取区域特性能量融合规则，如图8所示。

图7 不同方法的融合图像Fig.7 Different common methods of image fusion

表1 融合方法的客观评价Table 1 Objective evaluation of fusion methods

图8 不同规则的融合图像Fig.8 Image fused with different rules

客观评价函数指标与上述指标一致，评价指标数据如表2所示。

最后，再与参考文献中的融合规则进行比较，验证本文规则的有效性。选取的文献方法为：文献[5]中的融合规则，文献[8]中的融合规则。选取的客观评价函数指标与前面一致，将这两种融合规则与本文的融合规则作对比，如图9所示，表3是对应的客观评价数据表。

5.1 主观评价

以融合结果进行分析，图7中的4张图像，分别依次采用主成分分析法（PCA）、拉普拉斯金字塔（LP）融合方法、小波变换（WT）融合方法和小波-Contourlet变换（WBCT）融合方法，这4种融合方法。各图像间的亮度差距，无法利用人眼得出较为精确的结论；但各图像的亮度令观察者感到舒适，并不足以令观察者感觉到刺眼；亮暗对比度较高，场景信息丰富，细节纹理清晰，足以轻易地利用肉眼辨别出场景细节的变化程度；从使用者的主观角度出发，4张融合图像均取得令人满意的结果。

图8中的前3张图像是以Contourlet变换融合方法为基础，采用不同的融合规则融合而成；相比图7中的4张融合图像，亮暗对比度的变化程度并不剧烈，肉眼无法分辨；图像间的差别相差无几，难以分辨其中的差异；后3张图像是以小波-Contourlet变换融合方法为基础，采用不同的融合规则融合而成，融合规则的顺序与前3张图像的融合规则一致；后3张图像的前两张图像，与其余的图像较为相似，无法通过主观评价得出精准的差异结论；但不同之处在于，采用本文方法融合后的图像，相对而言整体的亮暗程度略微偏低，但清晰度依然良好，不妨碍观察，皆有良好的视觉效果，整体画面的观察舒适性依旧良好，场景信息与纹理细节皆较为充分；其次，从主观感官角度出发，此图像的亮度更适合人眼观察，观察舒适性更胜一筹，图7和图8剩余图像的亮度，对比之下，可能令观察者感觉略微刺眼。

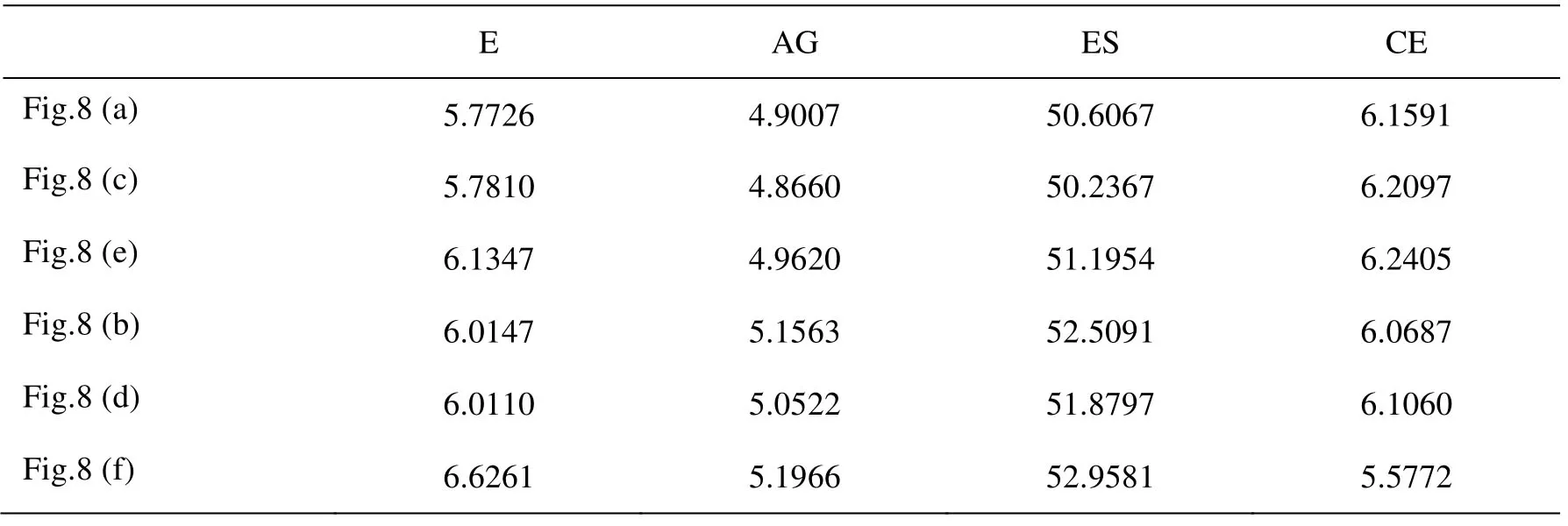
表2 融合规则的客观评价Table 2 Objective evaluation of fusion rules

图9 文献规则与本文规则的对比Fig.9 Comparison of documentary rules with the rules of this article

表3 文献融合方法的客观评价Table 3 Objective evaluation of literature fusion methods

图9皆是通过采用文献中的方法融合而成，相对于图7和图8的图像而言，通过文献提供的融合规则融合的图像，整体亮度皆偏暗，虽不妨碍观察，场景信息均清晰可见，但观察的舒适性进一步下降。与采用本文方法融合的图像对比，场景信息和纹理细节等差异颇小，但清晰度和舒适性皆略有所下降。

5.2 客观评价

通过分析实验测得的客观评价函数指标数据，可以得出以下结论：首先，表1中所反映的是，采用常用方法融合的图像的客观评价指标数据。依照融合图像的顺序，常用的融合方法依次为：主成分分析法、拉普拉斯金字塔融合方法、小波变换融合方法和小波-Contourlet变换融合方法。采用的客观评价函数指标为：信息熵（E）、平均梯度（AG）、边缘强度（ES）和交叉熵（CE）。在相同融合规则的前提下，图7(d)是采用WBCT方法的融合图像，其信息熵的数值为最高，远高于其余3种方法的融合图像，数值数据是最高的，表示图像7(d)所包含的平均信息量最丰富，融合质量最好。平均梯度反映了图像的整体清晰程度，能够较好地表达场景细节的灰度变化特性，边缘强度代表了场景边缘灰度变化程度的强弱，能够较好地反映出对比度以及微小灰度的变化；图7(d)的平均梯度与边缘强度的数值皆为最高，这意味着图7(d)相对于其他3张图像而言，最为清晰，纹理细节信息保留较为充分，场景目标的边缘清晰度为最高。交叉熵反映了两幅图像间的差异，数值越小，融合效果越好，图7(d)的交叉熵为最小，意味着该图像从源图像中提取的信息量最多。

其次，表2中反映的是，不同融合规则与本文融合规则的对比，以及Contourlet变换（CT）与小波-Contourlet变换（WBCT）的对比，两者相结合。在相同融合规则的前提下，利用WBCT方法融合的图像，在客观评价函数指标数据方面，皆优于采用 CT方法融合的图像；在相同的融合方法基础上，采用本文融合规则的融合图像，在信息熵、平均梯度和边缘强度这3个评价指标方面，皆比采用其余融合规则的融合图像更有优越性，在交叉熵上的表现略有差异。图8(f)是采用本文融合方法融合的图像，在评价数据上的表现，皆为最优，证明了本文融合方法的有效性和优越性。

最后，表3中反映的是，参考文献中提供的融合方法与本文融合方法的对比，文献[5]和文献[8]皆为典型的小波融合方法和剪切波融合方法。客观评价函数的数据表明，4个评价指标的数值皆为最优，验证了本文方法的有效性和优越性。

6 结束语

本文采用小波-Contourlet变换方法，对偏振强度图像和偏振度图像进行融合研究，通过3种不同方面的对比，验证了本文方法的有效性，依次为：常用融合方法的对比，融合规则的对比，与参考文献方法的对比。最后实验测得的客观评价函数指标数据表明，小波-Contourlet变换优于常用融合方法；融合规则的对比验证了本文融合规则的有效性；与文献方法的对比，验证了本文方法的优越性。最后，在人眼主观视觉上，图像的观察舒适性较好。