部分黏结FRP加固混凝土梁抗弯性能研究
2020-05-07张智梅黄庆彬
张智梅,黄庆彬
部分黏结FRP加固混凝土梁抗弯性能研究
张智梅,黄庆彬
(上海大学 土木工程系,上海 200444)
为研究部分黏结FRP加固方式对加固梁延性等抗弯性能的影响,建立部分黏结FRP加固梁的有限元模型,提出等效完全黏结FRP加固梁理论,即按照总变形相等的原则将部分黏结FRP 加固梁转化为等效的完全黏结 FRP 加固梁。数值分析结果表明:部分黏结FRP加固方式对加固梁的承载力影响不大,但随着无黏结长度的增加,梁屈服后的刚度有所下降,FRP的利用率和加固梁的延性均明显提高;等效完全黏结FRP加固梁与相应的部分黏结FRP加固试验梁抗弯性能吻合较好,利用等效完全黏结FRP加固梁理论进行部分黏结FRP加固梁的承载力和变形分析是可行的。
部分黏结;外贴FRP加固;混凝土梁;延性;FRP材料利用率

利用外贴FRP抗弯加固混凝土梁,可以显著改善梁的承载能力和刚度,已被国内外学者广泛认 同[1−6]。然而进一步分析现有研究成果可以发现,一方面,FRP加固后梁的延性明显低于加固前[2];另一方面,FRP早期剥离破坏是加固梁的主要失效形式[7−10],它不仅降低了FRP的利用率,而且使加固梁的延性和承载力均无法达到预期效果。低延性意味着加固梁破坏时会失去明显征兆,从而给加固梁埋下安全隐患。为此,如何使加固梁在获得承载力提高的同时保持必要的延性是值得探讨的一个问题。目前,国外学者[11−12]在试验研究的基础上,提出了部分黏结FRP的加固方式,即FRP仅在两端与混凝土可靠黏结,中间其余部分与混凝土之间无黏结,结果表明该加固方式可以有效改善加固梁的变形性能,并建立了相应的理论分析模型。国内仅有极少学者[13−14]也通过试验研究提出了相似观点。但现有关于部分黏结FRP加固梁的研究十分有限,理论研究更加缺乏。为此,本文首先利用数值模拟方法研究部分黏结FRP加固梁的承载力和变形性能,探究该加固法改善加固梁延性的有效性;其次提出等效完全黏结FRP加固梁的概念,建立部分黏结FRP加固梁的理论分析方法,从而为采用部分黏结FRP加固方式改善加固梁变形性能提供理论依据。
1 非线性有限元模拟
1.1 试验概况
为研究部分黏结FRP对加固梁性能的影响,本文选用文献[11]中的试验梁进行有限元模拟。试验梁的加载方式、截面尺寸、配筋情况及加固方式如图1所示,图中代表竖向外加荷载,表示FRP的无黏结长度。除对比梁外,试验包括2根无黏结长度分别为1 300 mm和1 700 mm的加固梁和1根完全黏结FRP加固梁。外贴FRP板材的截面尺寸为1.2 mm×30 mm,长度为3 200 mm,沿跨中对称布置,部分黏结加固时FRP仅在两端与混凝土通过黏结剂黏结,中间则为无黏结区域。为叙述方便,令L-X为加固梁的编号,L-0表示完全黏结FRP的加固梁。试验中各种材料的力学性能如表1所示。
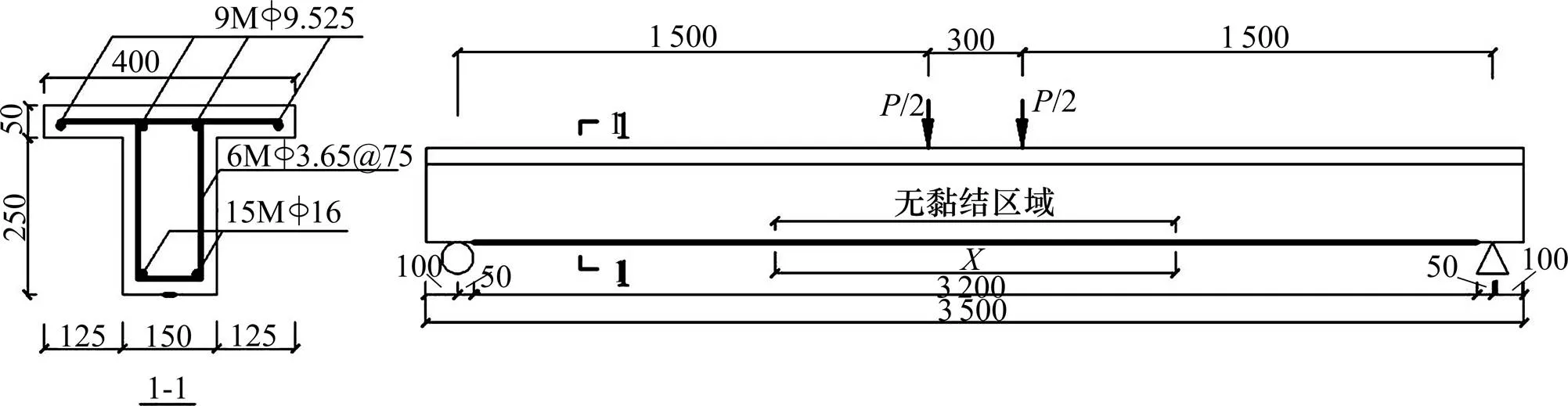
图1 梁L-X配筋及加固图

表1 材料的力学性能
1.2 有限元模型的建立
利用ABAQUS有限元软件对上述试验梁建立三维分析模型,并进行非线性数值分析。建模时,根据试验梁实际加固情况,假定钢筋−混凝土和FRP-混凝土界面均不发生黏结滑移。同时,为了避免产生应力集中现象,在支座处和跨中加载点处分别设置一个刚性垫块,如图2所示。
混凝土采用ABAQUS中的塑性损伤模型,其受拉和受压应力−应变关系分别选取混凝土结构设计规范[15](以下简称规范)中相应的混凝土受拉和受压本构;钢筋的本构采用规范中的双线性弹塑性模型;FRP为线弹性材料;垫块为线弹性材料,并按钢材设定。混凝土、钢筋、FRP的材料力学性能均按表1取用。混凝土、FRP和垫块均采用三维实体单元来模拟,单元类型为C3D8R;钢筋采用桁架单元模拟,单元类型为T3D2。
建模时,钢筋与混凝土之间采用内置(Embedded)约束,垫块与混凝土之间采用绑定(Tie)约束。FRP与混凝土之间,在黏结区域采用绑定(Tie)约束,在无黏结区域采用硬接触(Hard contact)以限制可能发生的FRP穿透混凝土的现象。在梁左、右两端的刚性垫块底部中线处分别按简支梁的受力特点设置边界约束。同时采用位移加载模式进行有限元分析。划分网格后的加固梁模型如图2所示。
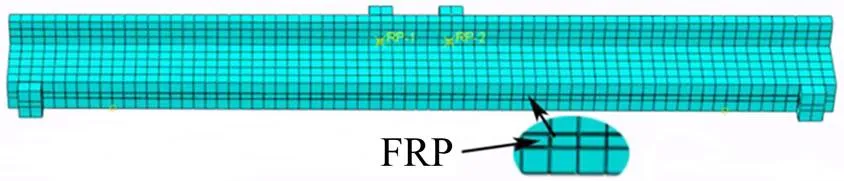
图2 有限元模型
1.3 有限元模型正确性的验证
按1.2节方法,对试验梁进行建模分析。图3为完全黏结FRP加固梁L-0及部分黏结FRP加固梁L-1300及L-1700的荷载-跨中位移曲线模拟结果,并与相应试验结果进行了对比。
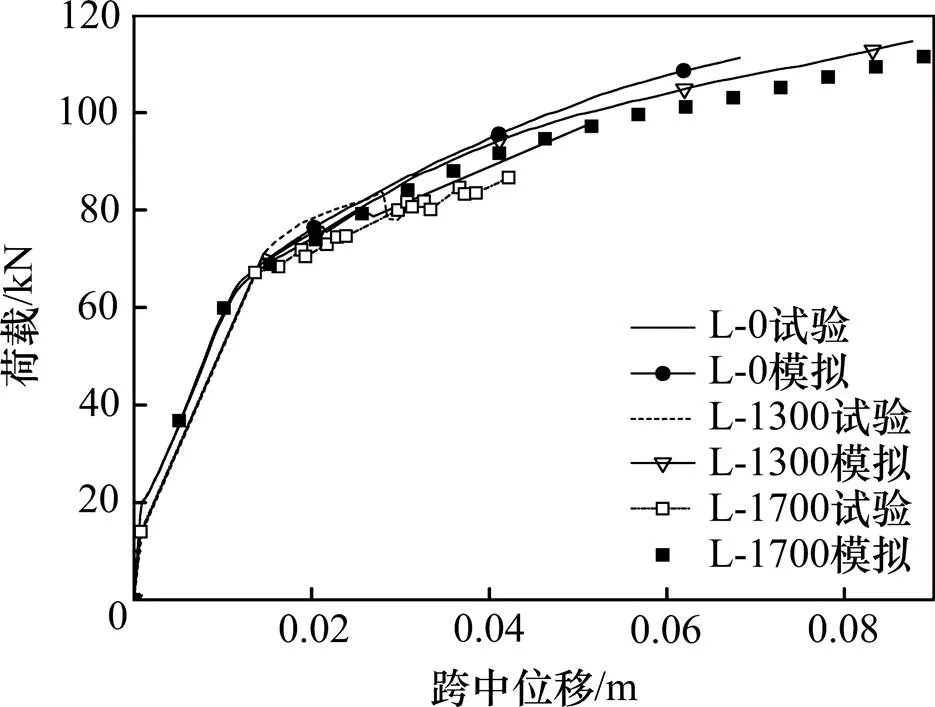
图3 荷载-跨中位移曲线
由图3可见,3根加固梁的荷载-跨中位移有限元模拟曲线在混凝土开裂前和开裂后至钢筋屈服阶段与试验结果基本吻合,仅在屈服后至极限破坏阶段存在一定分歧。这主要由于试验梁均因FRP过早发生剥离破坏而失效的,而本文模拟时假设界面不发生黏结滑移,故有限元分析得到的破坏荷载要高于试验值。由此可见,若能确保界面不发生早期剥离破坏,则本文所建立的有限元模型是正确可行的。另外,进一步分析图3可知,无论是试验还是数值分析,无黏结FRP加固梁的延性均较完全黏结FRP加固梁的延性有了较大提高。因此,在试验研究有限的情况下,有必要利用已验证的有限元模型进一步研究无黏结长度对加固梁延性等性能的 影响。
2 FRP无黏结长度对加固梁抗弯性能的影响
2.1 不同无黏结长度下加固梁的数值模拟
利用验证后的有限元建模方法,以加固梁L- 1300为基础,保持其他建模参数不变,仅在0~2 800 mm范围内改变FRP的无黏结区域长度,建立了多根部分黏结FRP加固梁的有限元模型,以研究无黏结长度对加固梁抗弯性能的影响。图4为各部分黏结FRP加固梁的荷载−跨中位移数值模拟曲线。

图4 加固梁的荷载-跨中位移模拟曲线
由图4可见,各加固梁的受力大致可分为3个阶段,即:开始受力到混凝土开裂前的弹性阶段,混凝土开裂后到钢筋屈服前的弹塑性阶段,以及钢筋屈服后至梁破坏的塑性极限阶段。虽然各加固梁的无黏结长度大小不一,但各梁的荷载−位移曲线在前2阶段几乎与L-1300完全相同,仅在第3阶段有较大差别,说明部分黏结FRP加固方式主要对加固梁屈服后的受力性能有较大影响。
2.2 无黏结长度对FRP应力分布的影响
通过有限元分析可以得到不同加载阶段FRP板上的应力分布情况,图5为部分加固梁破坏时的FRP应力沿板条长度方向的分布情况。
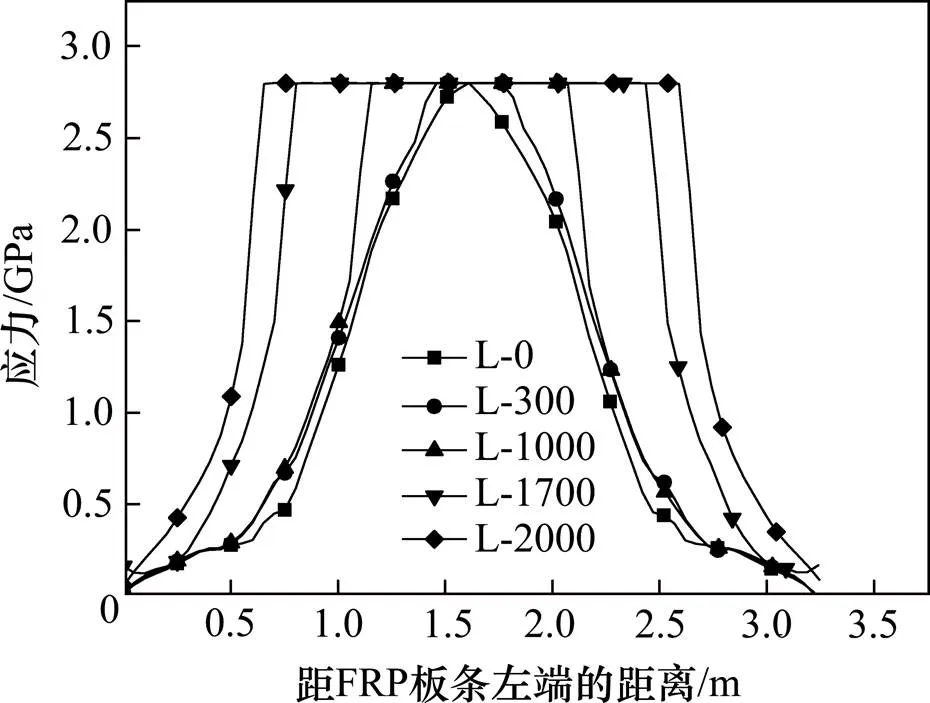
图5 梁破坏时FRP板条的应力分布
由图5可见,对于完全黏结FRP加固梁L-0,仅跨中位置的FRP应力达到其极限抗拉强度,离跨中位置越远,FRP应力越小。对于部分黏结FRP加固梁,随着无黏结长度的增加,FRP应力达到其极限抗拉强度的区域越大,且根据有限元分析结果可知,该区域长度与FRP的无黏结长度近似相等。又因FRP材料的线弹性特性,说明其应变发展也随无黏结长度的增加而越充分。综上所述,采用部分黏结FRP加固方式不仅可以有效提高FRP的利用率,而且随着无黏结长度的增加,FRP应力和应变充分发展的区域也越大,从而为加固梁的延性发展提供有利条件。
2.3 无黏结长度对加固梁承载力和延性的影响
为进一步分析部分黏结FRP加固方式对加固梁性能的影响,将2.1节中各加固梁的主要数值计算结果列于表2中。表中位移延性系数为各梁极限位移与屈服位移的比值。
由表2可见,从承载力角度看,无黏结长度对加固梁的屈服荷载几乎无影响,对其极限荷载的影响也不大。从变形性能角度看,无黏结长度对加固梁的屈服位移几乎无影响,但随着无黏结长度的增加,其极限位移却逐步提高,从而使得加固梁的位移延性系数也随之不断提高,相较于完全黏结FRP加固梁L-0,部分黏结FRP加固梁L-2800的延性系数增加了约141%,表明加固梁的延性性能有较大幅度提高。进一步分析图4中的荷载-位移曲线可以发现,加固梁第3受力阶段即屈服后的刚度亦随无黏结长度的增加而呈现逐渐降低趋势。综上所述,部分黏结FRP加固方式对加固梁的承载力影响不大,但随着无黏结长度的增加,其屈服后刚度有所下降,延性性能提高明显,从而提高了加固梁使用的安全性。
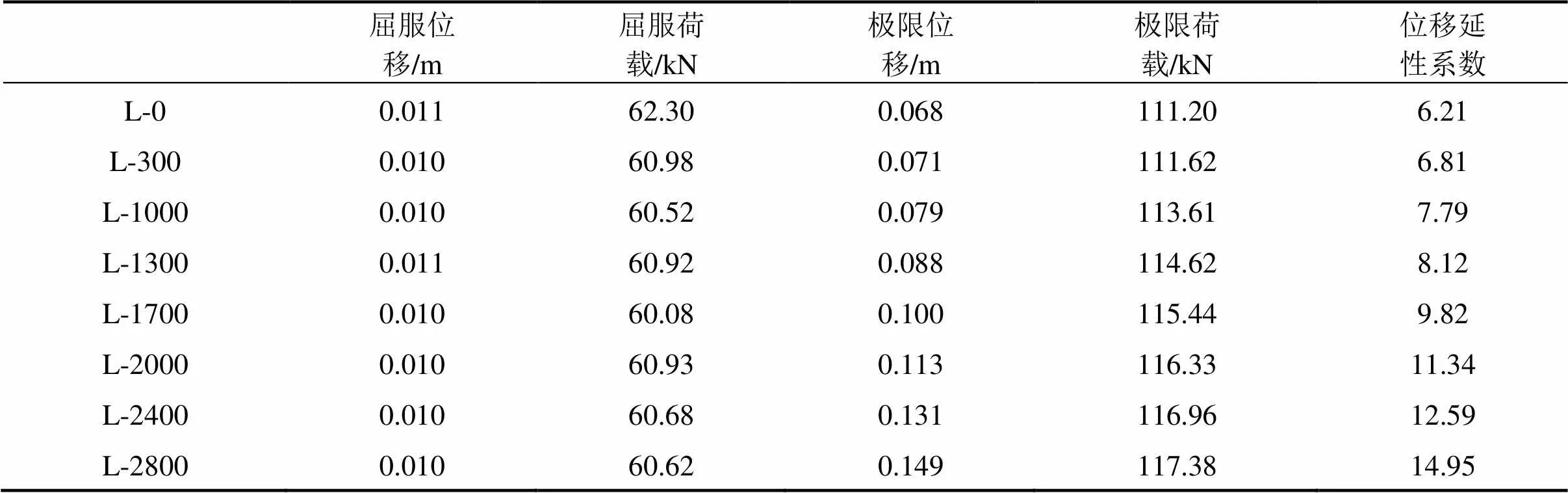
表2 主要计算结果和位移延性系数
注:梁L-X的无黏结区域长度为(mm)。
3 部分黏结FRP加固梁的理论分析模型
为进一步验证部分黏结FRP加固方式的有效性,引入等效完全黏结FRP加固梁的概念,建立部分黏结FRP加固梁的理论分析模型,以预测加固梁的受力性能。
3.1 理论分析模型的建立
对于部分黏结FRP加固梁,位于跨中无黏结区域的混凝土和FRP的变形因两者之间没有可靠黏结而不再协调,即平截面假定不再成立,因而无法用传统的截面分析方法来计算加固梁的承载力等性能。为此,本文进一步利用第1节建立的部分黏结FRP加固梁的有限元分析模型,探究FRP应变与混凝土应变之间的关系。限于篇幅,仅给出了部分黏结FRP加固梁L-1700破坏时的FRP拉应变和FRP长度范围内梁底混凝土拉应变的分布曲线,如图6所示。
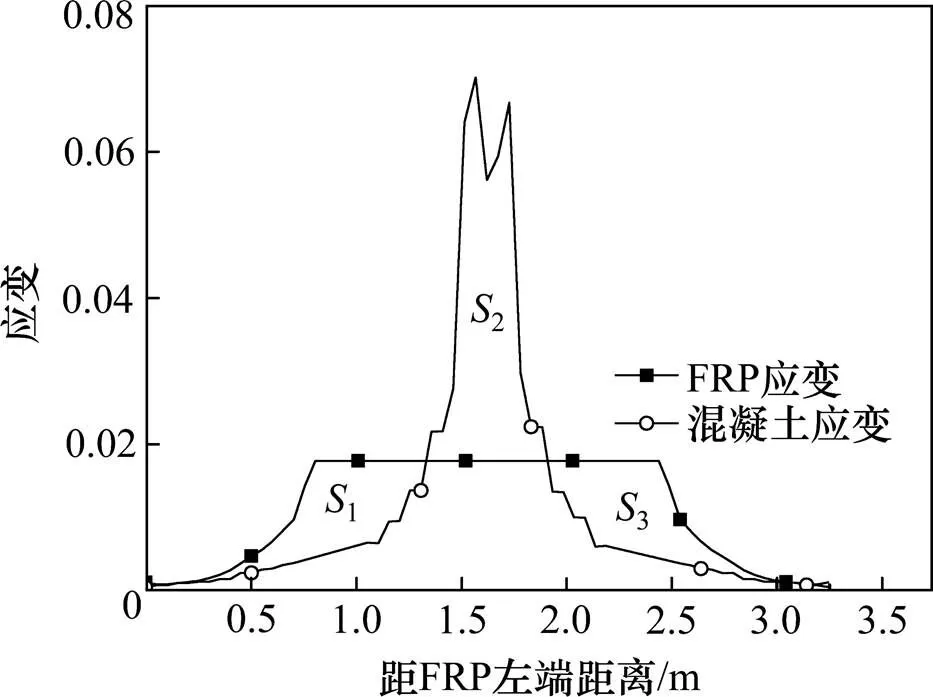
图6 FRP与混凝土应变分布
图6中,1,2和3分别为2曲线所围成的3个区域的面积,由图6可知,1与3之和与2近似相等,说明2条曲线与轴所围成的面积近似相等。因而对于部分黏结FRP加固梁而言,虽然不符合平截面假定,但是在FRP长度范围内可以认为FRP与混凝土的总变形近似相等。然而,若从总变形相等的角度去分析加固梁,会使问题变得十分复杂。
目前有关完全黏结FRP加固梁的计算理论已较为成熟,已有学者提出可对完全黏结FRP加固梁承载能力及变形直接计算的公式,且经验证,计算结果与试验结果相符较好[16]。如果设法将部分黏结FRP加固梁转化为完全黏结FRP加固梁,则可使部分黏结FRP加固梁的分析计算大大简化。
由图5可见,破坏时,完全黏结FRP加固梁L-0中FRP应变近似为三角形分布,而其余部分黏结FRP加固梁中FRP应变近似为梯形分布,其上底长度为无黏结区域长度。于是,按照总变形相等的原则将部分黏结FRP加固梁的梯形应变分布等效为完全黏结FRP加固梁的三角形应变分布,等效方法如图7所示。
则等效完全黏结FRP加固梁的FRP最大应变可按下式计算,即:
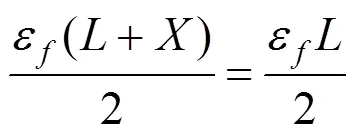
化简得:
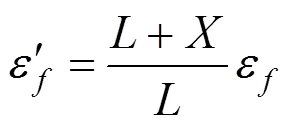
进一步地,为保证等效前后FRP板条的极限抗拉强度保持不变,可对等效前后FRP的弹性模量进行折减,即:
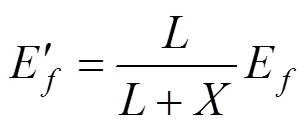
式中:和分别为等效完全黏结及部分黏结FRP加固梁破坏时FRP的弹性模量。
综上,基于总变形相等的原则,在不改变其他参数的情况下仅通过对FRP弹性模量进行折减,即可将部分黏结FRP加固梁转换为等效的完全黏结FRP加固梁,从而可以利用完全黏结FRP加固梁的计算理论来预测部分黏结FRP加固梁的承载力和变形等性能。本文称之为等效完全黏结FRP加固梁法。
3.2 理论模型的验证
为检验等效完全黏结FRP加固梁法的有效性,本文利用1.3节中已经过试验验证的加固梁模型进行分析。首先将FRP的弹性模量根据梁L-1300和梁L-1700的无黏结长度按式(2)由165 GPa分别折减至117.33 GPa和107.8 GPa;然后再分别以其作为等效完全黏结FRP加固梁L-0中FRP的弹性模量进行有限元分析。图8为等效完全黏结FRP加固梁的荷载−跨中位移数值分析曲线与相应的部分黏结FRP加固梁的试验结果对比。
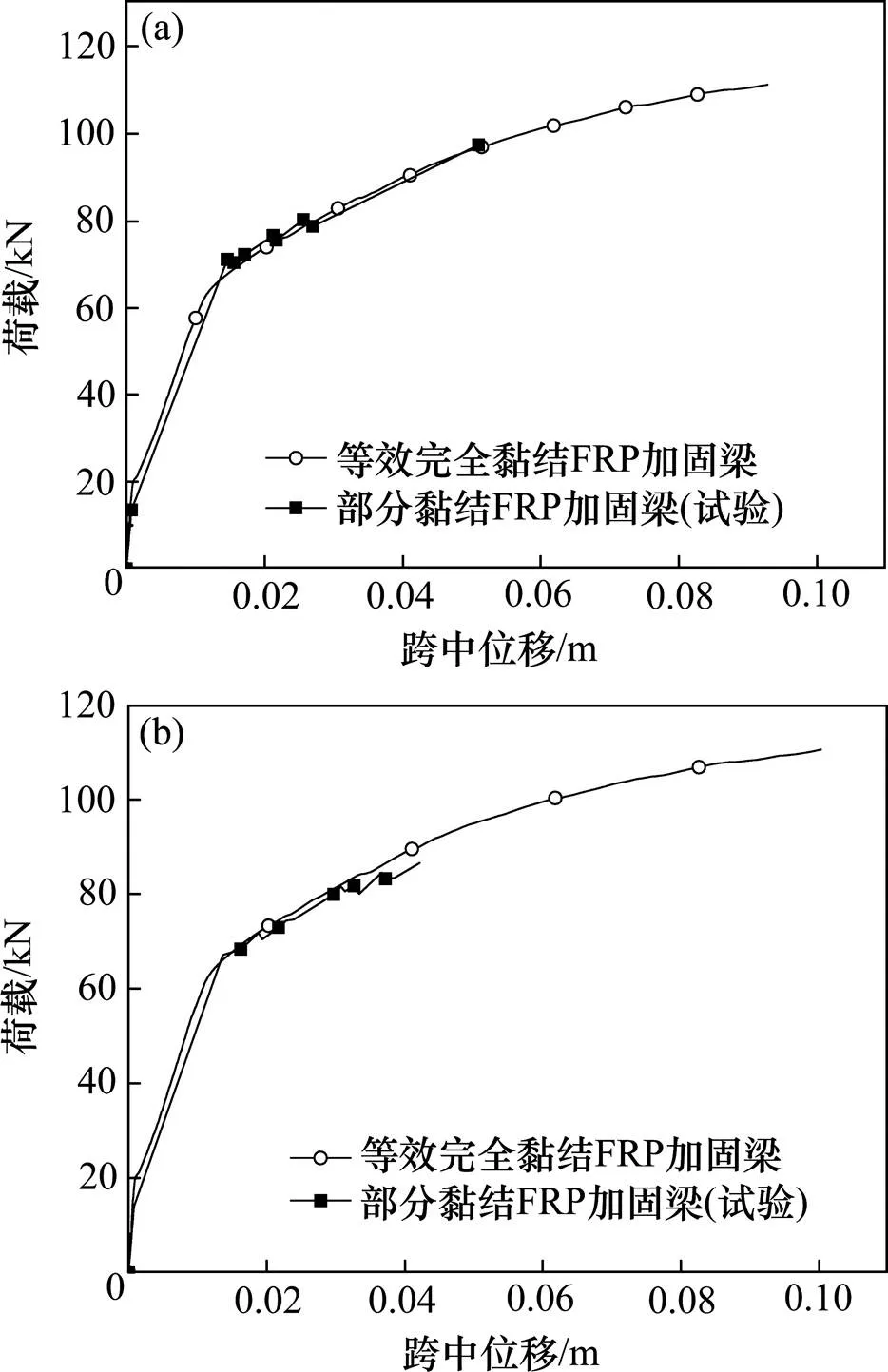
(a) L-1300;(b) L-1700
由图8可见,两者在试验梁发生剥离破坏前基本完全吻合,说明等效加固梁的承载能力及变形性能与部分黏结FRP加固梁近乎相同,等效完全黏结FRP加固梁法是有效的。因此,利用现有的关于完全黏结FRP加固梁的理论对等效完全黏结FRP加固梁的承载能力及变形性能进行分析计算,即可实现对相应的部分黏结FRP加固梁承载力及变形性能的预测。
4 结论
1)建立部分黏结FRP加固梁的有限元模型,数值分析结果表明:部分黏结FRP加固方式对加固梁的承载力影响不大,但随着无黏结长度的增加,梁屈服后的刚度有所下降, FRP的利用率和加固梁的延性均明显提高,从而改善了加固梁的使用安全性。
2)提出等效完全黏结FRP加固梁理论,按照总变形相等的原则,并对FRP 弹性模量进行适当折减,从而将部分黏结 FRP 加固梁转化为等效的完全黏结FRP加固梁。经试验验证,等效完全黏结与部分黏结FRP加固梁承载能力及变形性能相近,表明该等效方法有效可行。
3) 本文研究中未考虑FRP-混凝土界面之间的滑移,且加固量较小,今后需进一步考虑滑移和加固量变化时无黏结长度对部分黏结FRP加固梁性能的影响。
[1] 叶列平, 冯鹏. FRP在工程结构中的应用与发展[J].土木工程学报, 2006, 39(3): 24−36. YE Lieping, FENG Peng. Applications and development of fiber-reinforced polymer in engineering structures[J]. China Civil Engineering Journal, 2006, 39(3): 24−36.
[2] ZHANG S S, YU T, CHEN G M. Reinforced concrete beams strengthened in flexure with near-surface mounted (NSM) CFRP strips: Current status and research needs[J]. Composites Part B, 2017, 131: 30−42.
[3] 张智梅, 熊浩. 表层嵌贴预应力CFRP板条加固RC梁抗弯性能有限元分析[J]. 上海大学学报(自然科学版), 2018, 24(1): 100−107. ZHANG Zhimei, XIONG Hao. Finite element analysis on flexural performance of RC beams strengthened with prestressed near-surface-mounted CFRP strips[J]. Journal of Shanghai University (Natural Science Edition), 2018, 24(1): 100−107.
[4] 卜良桃, 肖喜平. 预应力碳纤维板加固 RC梁二次受力抗弯性能研究[J]. 铁道科学与工程学报, 2017, 14(1): 126−134. BU Liangtao, XIAO Xiping. Study on the flexural behavior of RC beams strengthened with prestressed CFRP under secondary load[J]. Journal of Railway Science and Engineering, 2017, 14(1): 126−134.
[5] 高仲学, 王文炜, 黄辉. 预应力碳纤维布加固钢筋混凝土梁抗弯承载力计算[J]. 东南大学学报(自然科学版) , 2013(1): 195−202. GAO Zhongxue, WANG Wenwei, HUANG Hui. Calculation of flexural capacity of RC beams strengthened with prestressed CFRP sheet[J]. Journal of Southeast University (Natural Science Edition), 2013(1): 195−202.
[6] Hamid R, Allan H. Concrete beams strengthened with externally bonded FRP plates[J]. Journal of Composites for Construction, 2001, 5(1):44−56.
[7] 吴业飞, 陈伟球. 基于内聚力模型的FRP-混凝土粘结强度分析[J]. 工程力学, 2010, 27(7): 113−119. WU Yefei, CHEN Weiqiu. Cohesive zone model based analysis of bond strength between FRP and concrete[J]. Engineering Mechanics, 2010, 27(7): 113−119.
[8] Kotynia R. Bond between FRP and concrete in reinforced concrete beams strengthened with near surface mounted and externally bonded reinforcement[J]. Construction and Building Materials, 2012, 32: 41−54.
[9] Hamidreza Tahsiri, Omid Sedehi. Experimental study of RC jacketed and CFRP strengthened RC beams[J]. Construction and Building Materials, 2015, 95: 476−485.
[10] Ali Chahrour, Khaled Soudki. Flexural response of reinforced concrete beams strengthened with end- anchored partially bonded carbon fiber-reinforced polymer strips[J]. Journal of Composites for Construction, 2005, 9(2): 170−177.
[11] Han Tae Choi, Jeffrey S West, Khaled A Soudki. Analysis of the flexural behavior of partially bonded FRP strengthened concrete beams[J]. Journal of Composites for Construction, 2008, 12(4): 375−386.
[12] Sharaky I A, Torres L, Sallam H E M. Experimental and analytical investigation into the flexural performance of RC beams with partially and fully bonded NSM FRP bars/strips[J]. Composite Structures, 2015, 122: 113−126.
[13] 亓路宽, 杨友林, 张治华, 等. 部分粘贴 CFRP加固钢筋混凝土梁的试验研究[J]. 公路, 2007(10): 21−26. QI Lukuan, YANG Youlin, ZHANG Zhihua, et al. Experiment and study on RC beams strengthened by bonding CFRP partially[J]. Highway, 2007(10): 21−26.
[14] 殷俊鹏. 部分粘贴CFRP加固钢筋混凝土抗弯构件的延性研究[D]. 淮南: 安徽理工大学, 2017. YIN Junpeng. Study on ductility of reinforced concrete flexural members strengthened with partially bonded CFRP[D]. Huainan: Anhui University of Science and Technology, 2017.
[15] GB50010—2010, 混凝土结构设计规范[S]. GB50010—2010, Code for design of concrete structures[S].
[16] 卜良桃, 宋力, 施楚贤.碳纤维板加固钢筋混凝土梁的抗弯试验和理论研究[J]. 建筑结构学报, 2007, 28(1): 72−79. BU Liangtao, SONG Li, SHI Chuxian. Experimental and theoretical study on flexural behavior of RC beams strengthened with carbon fiber plates(CFP)[J]. Journal of Building Structures, 2007, 28(1): 72−79.
Study on flexural behavior of partially bonded FRP strengthened RC beams
ZHANG Zhimei, HUANG Qingbin
(Department of Civil Engineering, Shanghai University, Shanghai 200444, China)
In order to study the effect of partially bonded FRP reinforcement method on the ductile and bending properties of strengthened beams, the finite element model of partially bonded FRP strengthened beams was established, and the theory of equivalent fully bonded FRP strengthened beams was put forward, which is based on the principle of total deformation being equal, the partially bonded FRP strengthened beam is transformed into the equivalent fully bonded FRP strengthened beam. The numerical analysis results show that the partially bonded FRP reinforcement method has little effect on the bearing capacity of the strengthened beam, but with the increase of the unbonded length, the stiffness of the beam decreases a little after yielding, and the utilization rate of FRP and the ductility of the strengthened beam are obviously improved. The bending behavior of the equivalent fully bonded FRP strengthened beam is in good agreement with that of the corresponding partially bonded FRP strengthened beam, it is feasible to analyze the bearing capacity and deformation of partially bonded FRP strengthened beams by using equivalent fully bonded FRP strengthened beam theory.
partially bonded; strengthened with externally bonded FRP; RC beam; ductility; utilization rate of FRP
TU375
A
1672 − 7029(2020)04 − 0965 − 07
10.19713/j.cnki.43−1423/u.T20190494
2019−06−09
上海市科技型中小企业技术创新基金资助项目(1305H165500)
张智梅(1972−),女,河南长葛人,副教授,博士,从事工程结构的抗火和加固的研究;E−mail:zhangzhimei@staff.shu.edu.cn
(编辑 阳丽霞)
