梁端碰撞效应对大跨高墩连续刚构桥易损性影响
2020-05-07张炳鑫郑史雄杨进李俊师新虎
张炳鑫,郑史雄,杨进,李俊,师新虎
梁端碰撞效应对大跨高墩连续刚构桥易损性影响
张炳鑫1, 2,郑史雄2,杨进2,李俊2,师新虎2
(1. 中铁第四勘察设计院集团有限公司,湖北 武汉 430063;2. 西南交通大学 桥梁工程系,四川 成都 610031)
西部山区连续刚构桥的主桥常常是高墩大跨,主桥与桥台或引桥的纵向刚度差异较大,导致在地震作用下,主桥与其两端的引桥(台)的动力响应不同步,从而发生梁端碰撞。以某大跨高墩连续刚构桥梁为背景,基于OpenSees平台建立其非线性有限元模型,选取100条实测随机地震动,引入拉丁超立方抽样、云图法以及概率地震需求模型基本理论,考虑梁端可能的碰撞作用,计算桥梁主要构件的地震易损性曲线,选用串联模型进行桥梁系统易损性分析,研究桥梁梁端碰撞效应对桥梁易损性的影响。研究结果表明:梁端碰撞作用对桥梁结构不同构件有不同的影响,考虑碰撞效应可以降低桥梁系统的损伤概率。
大跨高墩连续刚构桥梁;碰撞效应;地震易损性分析;云图法;概率地震需求模型

我国西南地区地形地势复杂,山谷较深,在修建公路、铁路时修建了大量的连续刚构桥。与此同时,我国位于欧亚地震带与环太平洋地震带之间,西部地区为地震多发区,近年来发生了汶川地震、芦山地震、宜宾长宁等多次较大的地震。地震成为威胁这些桥梁安全的重要因素,在地震作用下,一旦桥梁发生破坏,也会影响救灾能力[1],保证桥梁震后安全具有重要意义。大量震害调查表明,地震作用下梁端碰撞是桥梁发生破坏的一个重要因素,许多学者进行了深入研究[2−4]。在大震作用下,梁端碰撞作用不仅会导致桥梁结构的局部破坏,还可能导致支座失效,进而发生落梁。特别是大跨度高墩连续刚构桥梁,当其与小跨度引桥相连时,相邻两结构动力特性差异较大,在地震作用下主桥和引桥的响应不同步,梁端碰撞现象更容易发生。综合国内外研究现状,大部分学者采用确定性方法研究梁端碰撞作用对大跨高墩连续刚构桥梁抗震性能的影响,很少采用易损性方法研究梁端碰撞作用对桥梁抗震性能的影响。在实际工程中,地震动是非平稳随机过程,具有很强的不确定性,桥梁结构自身也存在很强的不确定性。因此使用易损性的方法考虑地震动的不确定性和结构参数不确定性,研究梁端碰撞对高墩桥梁抗震性能的影响具有重要意义。鉴于此,本文以西部山区典型的大跨高墩连续刚构桥梁为例,使用易损性方法中常用的云图法研究梁端碰撞效应对大跨高墩连续刚构桥梁抗震性能的影响,从而为类似桥梁抗震设计作指导。
1 计算模型的建立
本文的研究对象为西部山区中常见的大跨度双肢薄壁高墩连续刚构桥,其引桥动力特性与主桥有着较大差别,在地震动的作用下,桥梁结构体系容易发生主梁−主梁梁端碰撞、主梁-桥台碰撞。为研究这一现象,本文建立主桥与四跨引桥的有限元模型。
1.1 工程概况
某公路桥梁由460 m主桥与160 m引桥构成,460 m主桥采用(120+220+120 m)连续刚构桥,160 m引桥采用4×40 m简支T梁。全桥为平坡,无竖曲线与平曲线,桥面宽12 m,横坡为2%。总体平面布置图见图1。
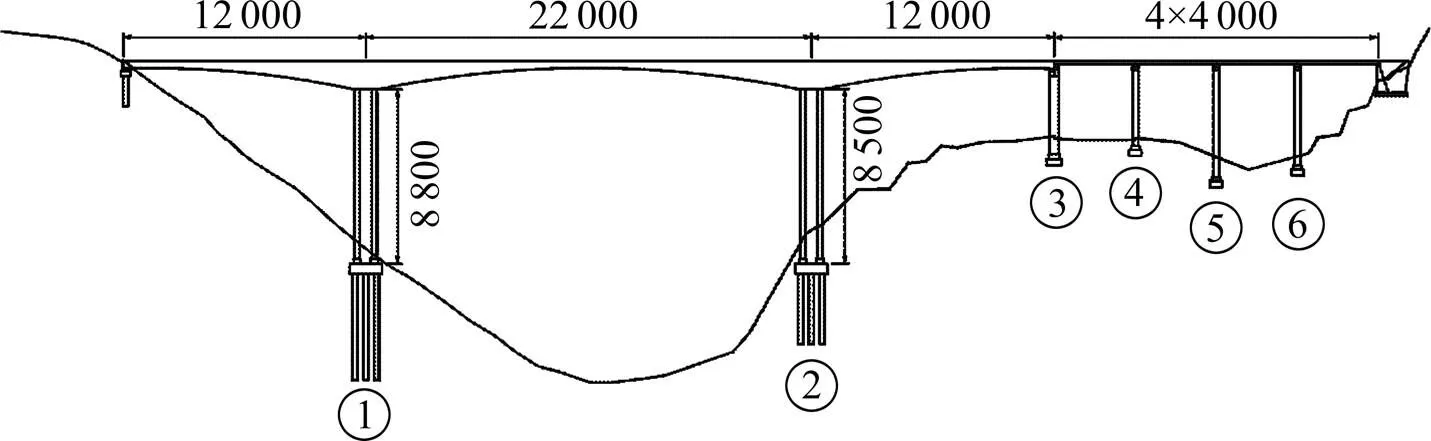
单位:cm
主桥上部为单箱单室箱梁,引桥上部为简支T梁,翼板有2%横坡。主桥桥墩为钢筋混凝土双肢薄壁墩,桥墩编号见图1,随着编号增加,里程增加,单薄壁厚3.3 m,双壁中距9.7 m。交接墩为壁厚3.5 m的钢筋混凝土空心墩。引桥桥墩均采用矩形钢筋混凝土空心墩。主桥桥台和过渡墩分别与主梁使用滑动支座连接,引桥简支梁中,每跨主梁与桥墩通过3个滑动支座和一个固定支座连接,固定支座设置在大里程中。
1.2 弹塑性动力响应计算模型建立
由于OpenSees软件不可视性,本文计算模型先使用Midas Civil建立,导出节点、单元等信息后,手动转化为OpenSees模型文件。
1.2.1 主梁和桥墩的模拟
本文使用弹性梁单元模拟主梁[5]。在OpenSees中,基于纤维单元的非线性梁柱单元可以定义钢筋、混凝土材料属性,同时可以定义截面的位置与面积,可以达到较为准确的模拟效果。本文对桥墩全部采用非线性材料模拟。混凝土材料使用OpenSees平台中基于Kent-Scott-Park模型[6]的Concrete02材料,钢筋使用OpenSees中的Steel02材料,其本构模型由Menegottto等提出与改进[7−8]。

图2 桥梁OpenSees有限元模型示意图
1.2.2 支座的模拟
本文结构模型中的支座是盆式橡胶支座,使用双线性理想弹塑性模型模拟[3],当支座的剪力超过最大摩擦力时,支座会发生滑动,支座的摩擦因数一般取值 0.02,其本构关系可见图2。对于多跨简支梁引桥,每跨桥梁中的4个支座中有一个支座为固定支座,固定支座3个方向设置较大数量级的刚度,达到约束自由度的效果。
1.2.3 碰撞单元的模拟
桥梁梁端碰撞作用模拟较为复杂,目前广泛使用接触单元法模拟。主要原理是在相邻的2个结构之间设置接触单元,当相邻结构接触后(即发生碰撞作用)接触单元才发挥作用。本文采用最常用的接触单元法模拟梁端碰撞作用。根据国内外学者研究,碰撞模型可以分为线弹簧模型、Kevin碰撞模型、Hertz接触模型、Hertz-damp接触模型、改进的Hertz-damp接触模型。Hertz-damp模型可以很好的考虑碰撞过程中的弹簧刚度变化和能量耗散,为了能够使用OpenSees软件模拟Hertz-damp碰撞模型,本文采用Muthukumar[9]提出的简化Hertz-damp碰撞模型,其本构关系见图3。
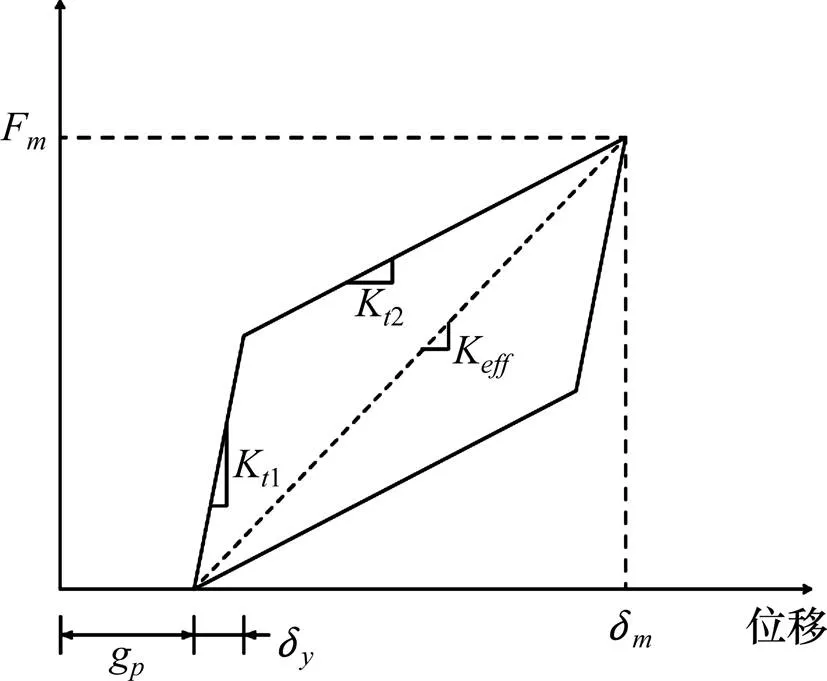
图3 简化Hertz-damp碰撞模型
模型中碰撞力的计算公式如下所示:
复杂分析对计算能力的需求超过了当时计算机的能力,为此兰德建造了自己的计算机。JOHNNIAC以数学家约翰·冯·诺依曼(John von Neumann)的名字命名,是最早带有存储内存的大型计算机之一。

式中:c为阻尼系数;K为碰撞模型中的弹簧刚度系数;1和2为2结构的位移;g为碰撞间隙宽度;为Hertz系数;典型取1.5。
简化后Hertz-damp碰撞模型在碰撞过程中能量耗散的计算公式为:

式中:为最大入侵位移;为恢复系数,通常取0.6~0.8。屈服位移常取最大入侵位移的0.1。
由简化碰撞模型与Hertz-damp模型的最大碰撞力相等,则简化碰撞模型的等效刚度为:

K为Hertz-damp模型的碰撞刚度,取值为结构的轴向刚度。等效刚度可以用初始刚度K1和应变强化刚度K2表示:
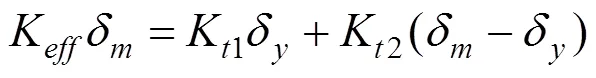
简化碰撞模型的力与变形曲线所围成的面积A可以用K1,K2和表示:

假设简化碰撞模型中力与变形曲线围成的面积近似等于结构碰撞过程中的能量耗散,可得到简化碰撞模型的刚度参数。
2 概率地震需求模型
地震易损性是指结构在地震动作用下达到或超过某种损伤状态的概率。目前计算易损性较常用的方法是使用大量非线性动力时程分析得到弹塑性桥梁结构动力响应[10],利用数学分析方法得到地震动强度与结构动力响应的关系。非线性动力时程分析方法主要有IDA方法、云图法等。IDA方法是对地震动强度进行一系列调幅,使用调幅后的地震动进行动力时程分析,得到不同地震动强度下的结构响应;云图法是直接使用若干地震动进行动力时程分析,由于分析结果呈云状,该方法被称为“云图法”[11],其相比于IDA方法,有计算量小的优点。故本文选用云图法计算桥梁构件易损性。
概率地震需求模型属于基于性能的地震工程研究,它表达了某一类型结构地震动强度与地震需求的概率关系。概率地震需求模型是概率地震需求分析的核心内容,其中地震需求可用式(6)表示:
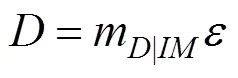


假设地震需求的中位值与地震动的强度服从指数关系[12],和为未知系数,则:
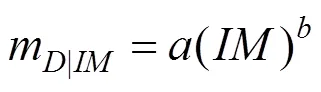

2.1 实测地震动选择
在进行概率地震需求分析时,需要选取大量天然地震动作为输入来考虑地震动的不确定性。地震动的不确定性对结构地震需求不确定性有着重要影响[13−14]。本文基于PEER地震动数据库,在较宽的震级范围与震中距范围内选取没有特殊性质的非近断层地震动,使地震动峰值加速度在一个较宽的范围均有分布,本文地震动选取100条,地震动峰值加速度范围从0.02~0.94,如图4所示。

图4 天然地震动的震级分布图
2.2 模型参数不确定性
影响概率地震需求模型另外一个重要的不确定性因素是桥梁结构模型参数的不确定性,这一不确定性因素可能是由建模误差、认知不完善所导致的[15]。本文整理了以往学者对模型参数不确定性的研究[16−17],建立了本文所使用的模型参数不确定性分布类型及参数,具体取值见表1。
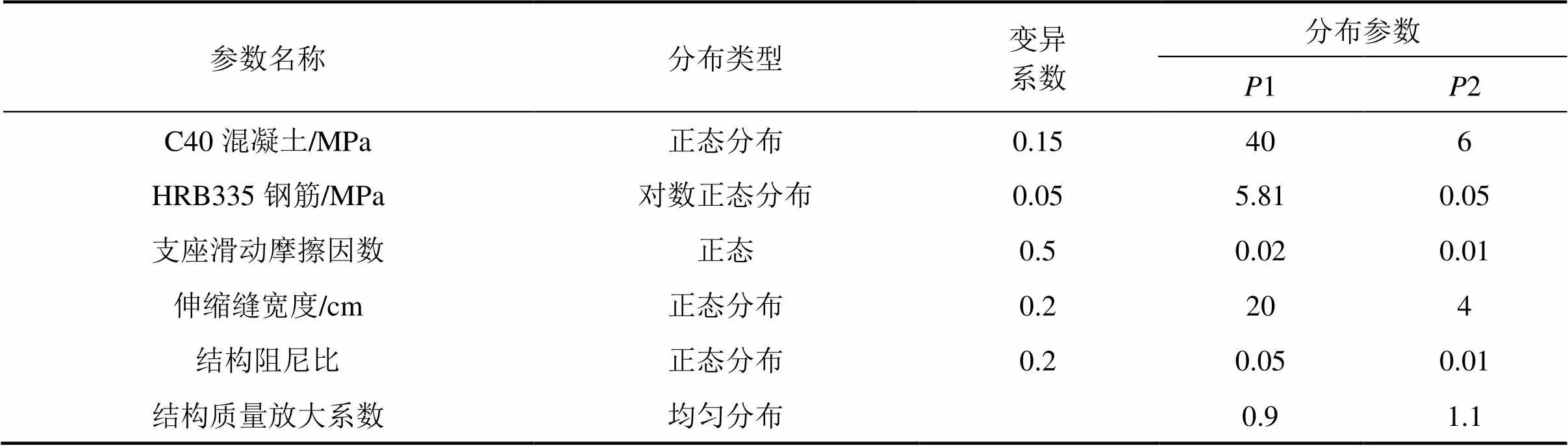
表1 模型不确定性参数分布类型及参数
3 极限状态分析
根据国内外学者研究方法,地震作用下桥梁构件可能处于5种状态,分别是无损伤、轻微损伤、中等损伤、严重损伤和完全损毁。
3.1 桥墩的损伤指标

3.2 支座的损伤指标
现有研究表明,在地震作用下桥梁构件中支座的损伤概率较高,支座损伤指标的选择较为重要。支座的损伤指标选择方式也有多种。在地震作用下,弹性橡胶支座多为剪切破坏,郑凯锋使用容许剪切应变作为损伤指标,Hwang使用支座剪力作为损伤指标[19],其他常用的损伤指标主要还包括位移延性比、支座位移等。根据本文模型实际情况,当支座的变形超过一定程度无法复原,支座发生损坏,本文采用支座位移为支座的损伤指标。支座损伤指标[1, 3, 20]具体取值见表3。

表2 桥墩纵桥向极限状态参数

表3 支座极限状态参数
3.3 极限状态的不确定性
本文假设桥墩墩底、支座的抗震能力服从对数正态分布,需要确定其对数标准差。部分学者将抗震能力对数标准差与概率地震需求模型对数标准差结合考虑,取固定值进行计算,本文参考Nielson相关研究,使用变异系数(COV)计算对数标准差,假设轻微损伤、中等损伤COV取值为0.25,严重损伤、完全损毁COV取值为0.5,抗震能力对数标准差可以使用(4-11)计算,计算结果见表4。


表4 构件极限状态不确定参数
4 易损性分析
使用确定参数结构模型,选取7条天然地震动,计算主要构件响应峰值平均值,研究发现1号桥墩、2号桥墩、交接墩考虑梁端碰撞作用后,其墩顶位移的放大系数分别为0.915,0.943和1.024,其墩底弯矩的放大系数分别为0.863,0.944和1.010,主桥桥墩墩底弯矩减小甚至达到14%,梁端碰撞效应对不同构件动力响应影响不同,应具体分析。
4.1 主要构件概率地震需求分析

交接墩墩底考虑碰撞效应与不考虑碰撞效应概率地震需求分析分别如图5所示。
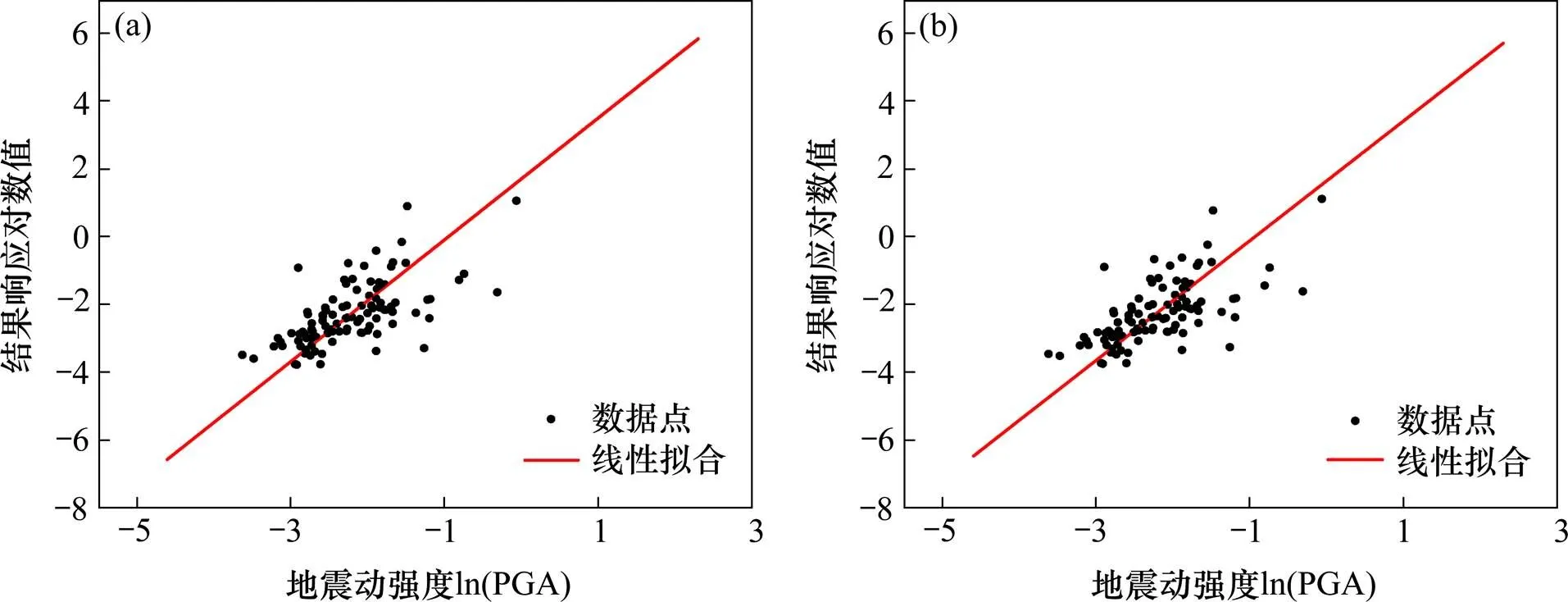
(a) 考虑碰撞;(b) 不考虑碰撞
4.2 构件易损性分析
构件易损性的计算需要考虑2种概率状态,分别是概率地震需求和抗震能力极限状态,将两者结合考虑,即为在确定的地震动强度下构件的概率地震需求达到或超过构件抗震能力极限状态的条件概率,可用(11)表示:



将式(8)代入(12)中,可得到:
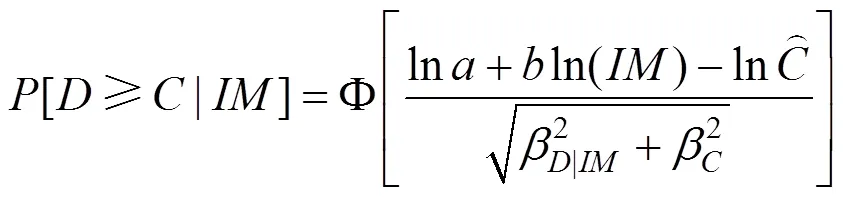
部分主要构件易损性分析如图6所示。
从图6可以看出,对于结构参数不确定性桥梁构件,考虑碰撞效应后,桥台处支座损伤超越概率有所增加,交接墩处支座损伤超越概率有所减小,1号桥墩损伤概率有所减小,而2号桥墩、交接墩的损伤概率均有所增加,说明碰撞单元对不同构件带来完全不同的影响效应,碰撞单元的作用效应不可忽视。对于主桥,两端边界条件不同,一端为刚性桥台,一端为多跨简支梁桥。对于刚性桥台,主要表现为能量耗散,与其靠近的1号桥墩动力响应减小,对于引桥,由于碰撞作用产生了碰撞力,导致2号桥墩、交接墩的损伤概率增大。

(a) 桥台处支座;(b) 主桥交接墩支座;(c) 1号桥墩墩底右肢;(d) 2号桥墩墩底右肢;(e) 交接墩墩底
4.3 桥梁系统易损性分析
桥梁系统损伤概率应使用串联模型进行计算,本节使用一阶界限法估算桥梁结构系统的损伤概率范围。对于使用串联模型的桥梁结构系统,每个构件的损伤概率为P。实际工程中,桥梁各构件相关系数处于0到1之间,系统失效概率也处于这2种情况下的系统失效概率之间:

本节选取桥梁系统中3个关键构件,根据已求解的构件损伤概率利用一阶界限法求解出桥梁系统的损伤概率范围,具体计算结果见图7。
从图7可以看出,在地震动强度较小阶段,考虑碰撞效应后得到的系统损伤概率下界小于不考虑碰撞效应的系统损伤概率下界。可以说明考虑碰撞效应能够降低系统的损伤概率。

(a) 轻微损伤超越概率;(b) 中等损伤超越概率;(c) 严重损伤超越概率;(d) 完全损毁超越概率
5 结论
1) 考虑梁端碰撞作用后,靠近桥台侧主墩损伤概率减小,交接墩的损伤概率增加。这是由于刚度不同动力响应不同步造成的,梁端碰撞作用会减小刚度较小的结构动力响应,碰撞力导致交接墩损伤概率增大。在结构设计中,应考虑梁端碰撞作用对交接墩带来的影响。
2) 桥梁系统使用串联模型进行易损性计算,在4种损伤状态下,桥梁系统的易损性均大于每个构件的易损性,直接使用主要构件的易损性评估桥梁系统的易损性是不合适的。
3) 考虑梁端碰撞效应可以降低桥梁系统的损伤概率。
[1] 陈银灯. 基于OpenSees软件的大跨度铁路斜拉桥系统地震易损性研究[D]. 成都: 西南交通大学, 2018. CHEN Yingdeng. Seismic vulnerability analysis of long-span railway cable-stayed bridge system based on OpenSees[D]. Chengdu: Southwest Jiaotong University, 2018.
[2] 高玉峰, 蒲黔辉, 李晓斌. 考虑碰撞效应的双柱式高墩桥梁非线性地震反应特性研究[J]. 公路交通科技, 2011, 28(4): 36−45. GAO Yufeng, PU Qianhui, LI Xiaobin. Nonlinear seismic response characteristics of bridge with double-column high-rise piers considering pounding effect[J]. Journal of Highway & Transportation Research & Development, 2011, 28(4): 36−45.
[3] 康锐. 基于多点地震激励的山区铁路高墩桥梁碰撞研究[D]. 成都: 西南交通大学, 2017. KANG Rui. Research on pounding of railway high-pier bridges under multi-supported ground motion excitations [D]. Chengdu: Southwest Jiaotong University, 2017.
[4] JIA H Y, LAN X L, ZHENG S X, et al. Assessment on required separation length between adjacent bridge segments to avoid pounding[J]. Soil Dynamics and Earthquake Engineering, 2019, 120: 398−407.
[5] ZHANG J, BI K, ZHENG S, et al. Seismic system reliability analysis of bridges using the multiplicative dimensional reduction method[J]. Structure and Infrastructure Engineering, 2018: 1−15.
[6] Yassin M Y M. Nonlinear analysis of prestressed concrete structures under monotonic and cyclic loads[D]. California: University of California, Berkeley, 1994.
[7] Menegotto M, Pinto P E. Method of analysis for cyclically loaded reinforced concrete plane frames including changes in geometry and non-elastic behavior of elements under combined normal force and bending [C]// Proceedings of the IABSE Symposium on Resistance and Ultimate Deformability of Structures, Lisbon, 1973: 15−22.
[8] Filippou F C, Popov E P, Bertero V V. Effects of bond deterioration on hysteretic behavior of reinforced concrete joints[R]. Berkeley: Earthquake Engineering Research Center, 1983.
[9] Muthukumar S. A Contact element approach with hysteresis damping for the analysis and design of pounding in bridges[J]. Georgia Institute of Technology, 2003.
[10] 郑凯锋, 陈力波, 庄卫林, 等. 基于概率性地震需求模型的桥梁易损性分析[J]. 工程力学, 2013, 30(5): 165− 171. ZHENG Kaifeng, CHEN Libo, ZHUANG Weilin, et al. Bridge vulnerabllity analysis based on probabilistic seismic demand models[J]. Engneering Mechanics, 2013, 30(5): 165−171.
[11] 于晓辉, 吕大刚, 王光远. 关于概率地震需求模型的讨论[J]. 工程力学, 2013, 30(8):172−179. YU Xiaohui, LÜ Dagang, WANG Guangyuan. Discussions on probability seismic demand models[J]. Engineering Mechanics, 2013, 30(8): 172−179.
[12] Cornell C A, Jalayer F, Hamburger R O, et al. Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines[J]. Journal of Structural Engineering-ASCE, 2002, 128(4): 526−533.
[13] Padgett J E, DesRoches R. Sensitivity of seismic response and fragility to parameter uncertainty[J]. Journal of Structural Engineering, 2007, 133(12): 1710−1718.
[14] Kwon O S, Elnashai A. The effect of material and ground motion uncertainty on the seismic vulnerability curves of RC structure[J]. Engineering Structures, 2006, 28(2): 289−303.
[15] Frangopol P D. Probability concepts in engineering: emphasis on applications to civil and environmental engineering[J]. Structure and Infrastructure Engineering, 2008, 4(5): 2.
[16] 宋帅. 考虑构件相关性的桥梁系统地震易损性分析方法研究[D]. 成都: 西南交通大学, 2017. SONG Shuai. A study on seismic fragility analysis of bridge system considering dependence among components[D]. Chengdu: Southwest Jiaotong University, 2017.
[17] 陈力波. 汶川地区公路桥梁地震易损性分析研究[D]. 成都: 西南交通大学, 2012. CHEN Libo. Seismic vulnerability analysis for highway bridges in Wenchuan region[D]. Chengdu: Southwest Jiaotong University, 2012.
[18] WU W, LI L, SHAO X. Seismic assessment of medium-span concrete cable-stayed bridges using the component and system fragility functions[J]. Journal of Bridge Engineering, 2016, 21(6): 04016027.
[19] Hwang H, LIU J B, Chiu Y H . Seismic fragility analysis of highway bridges[C]// Referenzmodellierung, 2001: 101−112.
[20] 李立峰, 吴文朋, 黄佳梅, 等. 地震作用下中等跨径RC连续梁桥系统易损性研究[J]. 土木工程学报, 2012, 45(10): 152−160. LI Lifeng, WU Wenpeng, HUANG jiamei. et al. Study on system vulnerability of medium span reinforcement concrete continuous bridge under earthquake excitation[J]. China Civil Engineering Journal, 2012, 45(10): 152−160.
Influence of pounding effects on seismic vulnerability analysis of the high-pier large-span continuous rigid frame bridges
ZHANG Bingxin1, 2, ZHENG Shixiong2, YANG Jin2, LI Jun2, SHI Xinhu2
(1. China Railway Siyuan Survey and Design Group Co., Ltd, Wuhan 430063, China; 2. Department of Bridge Engineering, Southwest Jiaotong University, Chengdu 610031, China)
High-pier large-span continuous rigid frame bridges have been extensively constructed in Western Mountain of China, and the longitudinal rigidity of main bridge and approach bridge (abutment) are quite different. It is prone to collision between girders or between girder and abutment because that the dynamic response of main bridge and approach bridge are nonsynchronous under earthquake. In this paper, a high-pier long-span continuous rigid frame bridge was taken as an example. Firstly, a nonlinear finite element model of the bridge was established with the help of OpenSees. Then, a large number of natural seismic waves were selected to analyze the vulnerability of bridge components and system. Seismic vulnerability analysis of the bridge was carried out by the Latin hypercube sampling, the cloud method and the basic theory of probability seismic demand model. Series model was chosen to analyze the vulnerability of this bridge system and the influence of pounding effect were studied. The results show that pounding has different effects on different member of bridge and the damage probability of bridge system can be reduced by considering pounding effect.
high-pier large-span continuous rigid frame bridges; pounding effect; seismic vulnerability analysis; cloud method; probabilistic seismic demand model
U44
A
1672 − 7029(2020)04 − 0891 − 09
10.19713/j.cnki.43−1423/u.T20190492
2019−06−03
铁四院软件研发课题(2018D001,2019D003);国家自然科学基金高铁联合基金重点项目(U1434205)
郑史雄(1965−),男,浙江江山人,教授,博士,从事桥梁抗风抗震研究;E−mail:zhengsx@home.swjtu.edu.cn
(编辑 涂鹏)
