基于阻抗的数字延时对单电流环控制型并网逆变器稳定性影响的分析

屠一鸣，刘进军，刘 增，薛丹红

（西安交通大学电气工程学院，西安 710049）

随着数字控制处理器的快速发展，目前电力电子变流器的控制系统普遍采用快速且更高效的数字控制方法。不同于模拟控制器，数字控制器由于采用离散实现方式，因此将不可避免地给控制系统引入延时环节，这包括采样延时、计算延时和PWM延时等[1，2]。工程上通常选择1.5倍的采样周期作为延时的大小，即采用e-1.5Ts对延时环节进行表征。而在模型计算以及设计上，通常采用其1阶帕德近似形式进行简化分析[3]。

数字控制延时会在变换器的控制环路中引入相位滞后作用[4]，这会降低控制环路的相位裕度和带宽，从而抑制控制系统的性能[5]。为了减小延时造成的影响，提高系统的控制性能，有学者提出了降低延时的方案。最直接的方法是采用非对称调制方法，即每个载波周期采样2次，这种方法可以将延时减小至0.75Ts[6]。另外，随着微处理器单元运算性能的提高，采样及控制算法运算所耗时间得以大幅减小。鉴于此，有研究提出了一种通过在每个采样周期内将采样时刻后移，从而减小处理器计算时值，实现减小整体延时的方法[7]。

近年来，有关数字控制延时效应的研究主要集中在对含有LCL滤波器的并网逆变器的稳定性分析[8-12]。首先，文献[8]建立了一个考虑延时的逆变器z-域离散小信号模型，用于预测电流控制环的稳定性；有学者在s-域建立了连续小信号模型，并提出了一个LCL滤波器谐振频率fres的概念，该频率为采样频率 fs的 1/6，如果 fres高于（1/6） fs，则为了确保系统稳定LCL谐振峰的幅值不能够低于0 dB[9]，fres=（1/6）fs，则对于采用电容电流反馈的有源阻尼控制方法，无论控制器系数如何改变，系统始终保持不稳定[10]；文献[11-12]则分别针对基于逆变器测电流和基于网侧电流反馈这两种控制结构下延时对LCL型并网逆变器稳定性的影响进行了分析,得出了确保系统稳定的延时取值范围。综上，现有研究中对延时效应的分析均是首先通过推导系统的控制框图获得控制环的环路增益，进而通过幅值裕度 GM（gain margin）和相位裕度 PM（phase margin）、根轨迹分布或者奈奎斯特图等方法来判断系统的稳定性。

尽管基于系统环路增益的方法能够有效判断并网系统的稳定性，但基于阻抗判据的方法来判断交流系统稳定性更为便捷，后者无需获得系统内部的确切信息，仅需获得端口的阻抗即可[13]。目前，采用基于端口阻抗的方法分析并网逆变器稳定性问题的研究主要集中在对LCL滤波器[14-15]、弱电网[16-17]、锁相环[18-19]和直流电压环动态[20]等因素的分析上。其中，锁相环动态对逆变器αβ坐标系[18]和dq坐标系[19]输出阻抗形状的影响，以及直流电压环动态对逆变器dq坐标系输出导纳[20]形状所造成的改变均已得到详细分析。然而数字控制延时作为决定系统稳定与否的重要因素之一，其对逆变器输出阻抗形状造成的影响，例如：延时是否仅影响逆变器输出阻抗的相频特性，抑或会同时影响阻抗的幅频和相频特性；延时具体会影响阻抗的哪一频率段等诸多问题，目前尚不清楚，亦缺乏相关研究对其详细讨论。

为了解决上述问题，本文的创新工作包括以下2个部分：

（1）本文首次发现并解释了由数字控制延时导致的、在逆变器dq系输出阻抗中存在的阻抗谷现象，并详细分析了延时及电流环控制参数对阻抗谷的幅值和相位特性产生的具体影响。

（2）本文提出了一种从阻抗角度来分析延时效应对并网逆变器系统稳定性影响的新思路。不同于现有文献中仅依据系统环路增益的传递函数来进行判断的方法，本文所采用的方法通过观察阻抗形状的变化并依据阻抗稳定判据来分析数字控制延时对系统稳定性的影响。

本文首先依据现有的单电流环控制型逆变器的输出阻抗模型，对比了有无延时情况下的阻抗；接着提出了阻抗谷的概念，并从数学的角度采用复频域表征的方式解释了其来源；然后详细讨论了阻抗谷与控制参数和延时大小之间的关系；再通过dd通道阻抗匹配和广义奈奎斯特判据分析了阻抗谷对并网逆变器稳定性的影响，并通过实验对上述理论分析加以验证；最后总结了延时效应所造成的阻抗谷对逆变器输出阻抗和系统稳定性影响的规律。

1 逆变器输出阻抗模型

为了研究延时引起的阻抗谷现象，首先要确定此现象是实际存在的。因此需要获得逆变器阻抗的精确模型，并通过在有无延时2种情况下的dq系阻抗对比图来判定。

1.1 系统描述

三相单电流控制型逆变器的单相等效拓扑以及控制结构如图1所示。图中，逆变器的直流侧由恒定电压源Vdc与电容器C并联供电；逆变器的交流侧通过滤波电感L连接到具有L-C型阻抗的弱电网Vg；逆变器侧输出电流iLabc在dq旋转坐标系下进行控制，其中相位信号θ通过检测公共耦合点PCC（point of common coupling）的电压 vpcc进行锁相获得，电流环采用传统的比例积分PI（proportion integration）调节器。

1.2 dq系输出阻抗建模

逆变器的阻抗建模过程分为2步：首先是对逆变器的主电路进行小信号线性平均化，获得主电路的小信号模型，如图2所示；其次是结合主电路与控制环节获得逆变器闭环系统的小信号等效框图，如图3所示，并依据框图推导输出阻抗模型。图2中，由于逆变器直流侧电压恒定，因此其小信号扰动量vdc为0，直流环的动态不会被引入到阻抗模型中。图3中所有传递函数均为2×2矩阵形式，其中Giv为开环输出导纳，Gid为占空比扰动到输出电流响应的开环传递函数。

由图2可得

式中：ω0为基波角频率；Vdc为逆变器直流侧电压。

图3中，Hi和Gdel分别为电流环PI控制器传递函数矩阵和延时传递函数矩阵，其表达式分别为

式中：kip和kii分别为电流环控制器的比例系数与积分系数；Ts为采样周期。

进而可以获得逆变器的输出阻抗为

式中，I为单位矩阵。若不考虑延时环节的影响，则输出阻抗可简化为

本文所研究的逆变器和控制器参数如表1所示。将表中数据代入式（5）和式（6）可得在考虑与不考虑延时环节时逆变器的dq阻抗波特图，如图4所示。由图4可见，当考虑延时环节后，逆变器输出阻抗的副对角线元素Zdq和Zqd发生变化，而在逆变器输出阻抗的主对角线元素Zdd和Zqq高频区域存在着明显的幅值跌落现象，从幅值上看，此现象类似于1个波谷，故本文称其为阻抗谷。同时相位从0°陡升至100°附近。

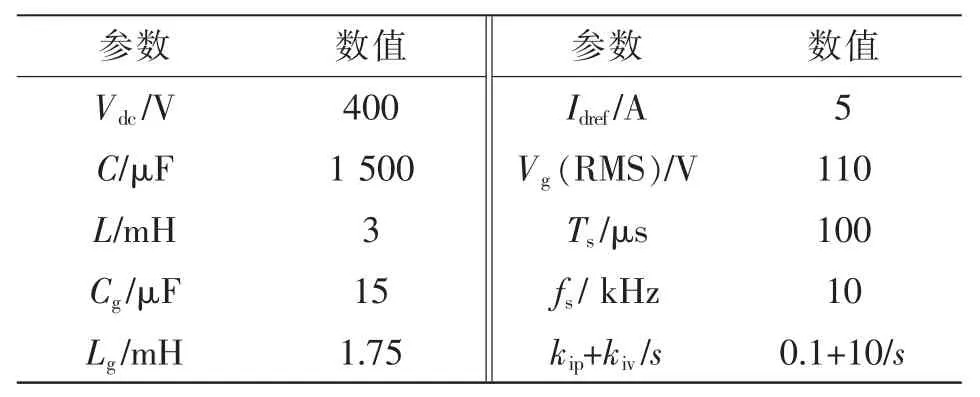
表1 逆变器元件及控制器参数Tab.1 Parameters of components and controller of the inverter

2 阻抗谷的来源

传统对延时的研究均从系统的环路增益出发进行分析，本文选择图3中的传递数的d-d通道项元素，从而获得系统标量形成的环路增益T，其表达式为

从延时的数学标量表达式Gdel=e-1.5sTs来看，其幅值为1，且相位随着频率的增大而逐渐减小。

Gdel、G1、G2和Zdd的波特图如图 5 所示， 图 5（a）中，Gdel其幅值为0 dB，相位随着频率升高线性衰减。Gdel、G1、G2和 Zdd的复频域如图 6 所示。从复频域图6（a）可见，延时为一个顺时针旋转的单位圆。因此当延时函数与其他传递函数相乘时，仅会引起高频相位衰减。而在逆变器输出阻抗表达式（5）中，延时矩阵不仅与其他传递函数矩阵相乘，其乘积还与单位矩阵I相加。当延时与某个常数，如单位常数1，进行相加时，定义G1为

由式（8）可见，G1随频率周期变性化，且每当1.5ωTs=π+2kπ（k=0，1，2，…）时，G1=0，其波特图幅值无意义。如图5（b）所示，每当达到式（7）频率处，G1幅值出现一个负尖峰，相位从-90°跳变至90°。而图6（b）更加直观地反映此过程，G1是一个以（1，j0）点为圆心、顺时针旋转的单位圆。每当曲线经过原点 P时，G1的模值为 0，相位角从-90°跳变至90°。同时，原点P的频率可以计算得到，即

倘若延时Gdel与除1外的其他任意常数进行相加，例如0.75，则定义G2为

同理，如图 5（c）所示，G2的波特图亦会出现周期性的幅值跌落现象，但此时相位突变程度减小，反映在图 6（c）复频域上，G2是以点（0.75，j0）为圆心的单位圆。在此单位圆轨迹上，亦存在一个位于（-0.25,j0）处的点 P'，且每当曲线绕过此点时，其模值先减小后增大，而相位发生跳变。

由图4可知，阻抗谷现象仅出现在Zdd和Zqq同时，由于系统三相对称，Zdd与Zdd相同，因此只需选择其一进行分析。以Zdd为例，通过推导可得Zdd为

Zdd的波特图如图5（d）所示，其在高频区域存在着周期性的幅值跌落与相位突升现象，尽管这一现象随着频率的进一步升高而逐渐衰减。而在复频域中，如图6（d）所示，Zdd是沿着虚轴方向循环出现的拱形，在每一段上总是存在着这样一个Pn点。在此点处，曲线的模值为整段拱形中的最小值，且相位发生突升。

考虑到小信号滑动平均建模方法的准确性，阻抗模型的准确度只能确保在1/2开关频率范围以内。由于本文所研究的逆变器开关频率fs为10 kHz，因此模型的准确度范围在5 kHz之内。在图5（d）波特图中，仅第 1个阻抗谷有效，在图 6（d）复频域中仅第1段拱形是有效的。

由式（11），Zdd由2部分组成，即电感sL以及与延时相乘的第2部分。电感sL是位于虚轴上的一条直线，而第二部分则近似为圆形。 因此，复合曲线是逆时针旋转90°的拱形，如图7（a）所示。若不考虑延时，则曲线即为一条与虚轴平行的直线，由sL向右平移获得，其幅值最小点即为起始点P0。若考虑延时，则存在P1这样的具有明显幅值转折的点。

3 阻抗谷的特征

从式（12）中可以发现，逆变器输出阻抗Zdd与电感L、直流侧电压Vdc、电流环比例系数看 kip，积分系数kii以及延时大小Tdel均相关。考虑到在实际应用场合中，主电路参数，例如电感及直流侧电压均保持不变，本文亦忽略这2个变量的影响，仅考虑电流环控制参数和延时大小。

由图5（d）可以发现，阻抗谷现象位于1 kHz附近，而电流控制环中积分算子的影响集中于低频区域，故可对式（11）进行简化，即

图8给出了Zdd与Zdd1的波特图，由图可见，积分算子kii的作用仅体现在12 Hz以下的频率区域，并不会影响阻抗谷，故在分析阻抗谷特性时可将其忽略。

同时，为了对阻抗谷进行解析分析，需对延时环节采用一阶帕德近似来替代进行简化，可得Zdd的简化表达式为

阻抗谷极值点处的频率定义为ωc，可通过对阻抗的模值进行求导获得，即

由式（14）可知，极值点频率ωc随着电流环比例系数kip的增大而增大，而随着延时Tdel的增大而减小。 图9展示了Zdd在3组kip（0.05、0.10和0.15）下的波特图。由图9可见，随着kip的增大，阻抗谷处的幅值下降更深，形状更为尖锐且相位突升更加严重，同时极值点频率ωc逐渐增大。图9中阻抗谷随着kip增大变得更严重的现象可以通过图10所示的复频域图更直观地进行解释。随着kip的增大可以发现，式（11）中的第2部分即延时所构成的圆的半径将增大。随着半径的增大，每条阻抗曲线上的模值最小点P1、P2和P3离原点的距离逐渐变小，因而反映在波特图中即为阻抗谷变得更深。此外，由于此转折点离原点近，因此当曲线绕过此点时，从第一象限进入到第二象限所需过渡的频率范围将大幅减小，使得相位突升现象变得更加严重。

图11为 Zdd在 Tdel=120、150 和 180 μs 情况下的波特图。随着Tdel的增大，同样阻抗谷的幅值也逐渐变得更深、且相位突升变得更加严重，但此时阻抗谷的极值点频率ωc将逐减小。延时大小的改变导致阻抗谷发生的变化亦可用复频域图来进行解释，如图12所示。随着延时数值的增大延时所构成的圆的旋转角速度增大，导致在合成阻抗时随着频率的增加，可能会出现sL的增大幅度小于延时圆的减小幅度的情况，因而曲线逐渐下移。同时，由于延时圆的旋转角速度加快每个拱形的周期将会变短，并且最小幅值点会在更低频率处出现。

4 稳定性分析

基于dq系阻抗来判断三相并网逆变器系统是否稳定的充分必要条件是广义奈奎斯特判据GNC（generalized Nyquist criterion）。此判据需首先获得逆变器侧与网侧阻抗的回率矩阵的特征值，进而依据特征值的奈奎斯特曲线是否围绕（-1，j0）点来判断系统是否稳定。然而，对于高功率因数或者单位功率因数系统，有研究称仅通过d-d通道阻抗即可判断阻抗匹配情况，且该方法能够大幅简化分析过程[15]。本文所研究的逆变器与L-C型电网的d-d通道阻抗匹配情况如图13所示。随着kip由0.05增大至0.15逆变器阻抗谷的幅值变得更深，且与电网阻抗Zgdd的相角裕度由25°减小到-45°左右。其中，当kip=0.1时，系统处于临界稳定状态。图14展示了回率矩阵特征值的Nyquist图，其稳定性判定结果与采用d-d通道阻抗判据一致。

同理，当延时Tdel改变时，系统的稳定性亦可采用这2种方法进行判断，在这种情况下逆变器与电网的d-d通道阻抗匹配情况如图15所示。随着Tdel由120 μs增大至180 μs，逆变器阻抗谷变得更深，与电网阻抗Zgdd的相角裕度由55°减小到-40°，系统在Tdel=150 μs时处于临界稳定状态。值得注意的是，当Tdel=180 μs时逆变器与电网阻抗相交的频率反而低于Tdel=150 μs的二者相交频率，这正体现了阻抗谷随延时增大极值点频率减小的特性。

在延时变化情况下采用GNC分析的结果如图16所示。当Tdel=150 μs时，奈奎斯特曲线穿过（-1，j0）点，系统临界稳定；当 Tdel减小至 120 μs ，系统恢复稳定，曲线不绕过（-1，j0）点；而当 Tdel增大至180 μs 时，系统失稳。

5 实验验证

实验验证环节需先后测试电流环比例增益kip及延时Tdel改变情况下的波形。实验所采用的参数如表1所示，验证步骤与前述模型分析相同。首先保持延时 Tdel恒定为150 μs，当改变kip时，测量出的波形如图17所示。当kip=0.05时，PCC点电压及电感电流均稳定。当kip增加至0.10时，系统临界稳定，所测波形出现较小幅值的振荡。而当kip继续增加至0.15时，系统出现严重振荡波形，这一结果与图13和图14中的结果吻合。

在图17（b）稳定的基础上，当改变延时Tdel大小时，实验测量结果如图18示。当Tdel减小到120 μs时，系统恢复稳定，从测量波形可以发现，此时控制效果更佳；而当Tdel增加到180 μs时，系统发生严重振荡，即将出现发散性振荡，图18（b）截取了即将发生发散振荡的波形，这一实验结果与图15和图16相吻合。

6 结语

本文发现并解释了因数字控制延时导致的在单电流环型逆变器输出阻抗中存在的阻抗谷的现象，并从阻抗判据的角度分析了延时对单电流控制型并网逆变器稳定性的具体影响。文章采用数学方法从理论上解释了阻抗谷的来源，进而又分析了该阻抗谷随参数变化的规律及对系统稳定性的影响。由于延时在频域中呈周期性变化，使得逆变器输出阻抗Zdd和Zqq在其高频范围处产生幅值跌落及相位突升的现象，故其称为阻抗谷。随着电流环比例增益kip和延时Tdel的增大，阻抗谷的幅值跌落及相位突升将愈加严重，使得逆变器阻抗与电网阻抗两者发生不匹配，进而导致并网系统产生高频振荡的不稳定现象。