基于CIR模型的数值模拟及设参保正对比分析

高世磊 李安琪 何佳璐 袁恒 张家铭

摘   要：隨机微分方程在金融数学中有很多应用，我们对用来分析利率的CIR模型进行了数值对比研究。我们分别对原方程用Euler算法的显隐式格式、Milstein算法的显式格式和对原方程进行变换后的格式以及应用分裂算法进行对比计算，主要对CIR模型中常数参数赋值进行数值模拟，并比较三种格式的方差。最后研究了CIR模型各算法的保正性。

关键词：CIR模型  Euler算法  Milstein算法  分裂算法  保正性

1  CIR模型简介

在20世纪80年代中期，Cox、Ingersoll和Ross对一个简单而又完备的经济体提出了一个时间连续的广义均衡单因子模型，并且用它来检验资产价格的行为[1]。基于对利率期限结构的研究，建立了CIR模型，利率的随机微分方程为一个单平方根过程：

其中回复速度α，长期均值μ和波动率σ均为常数参数。由上式可知，利率在长期均值μ附近上下波动，参数α表示利率回复到μ的速度，CIR模型将利率的波动设定为与利率水平的平方根成正比，波动率的方差会随着利率本身的增大而增大。该模型对任意时刻s，t（s≤t），当已知s时刻的短期利率信息时，时刻t的瞬时短期利率服从非中心卡方分布。

CIR模型中通过设定波动率与利率的平方根成正比，使得短期利率具有非负性：当→0时，漂移项α（μ-）为正值，且扩散项σ逐渐趋近于零，表明利率的波动性也趋近于零，因此利率不会取到负值;当2αμ<σ2时，CIR过程可以达到零界限值，当2αμ≥σ2时，向上的漂移项足可以使得零界限值无法达到，严格为正[2]。

2  CIR模型的三类格式及数值模拟

本小节是对CIR模型利用各种方式得到的数值方法进行数值求解并进行统计性质的对比和对CIR模型中常数参数赋值进行数值模拟。

2.1 第一类基本算法

2.3 分裂格式

2.4 参数赋值及统计特征

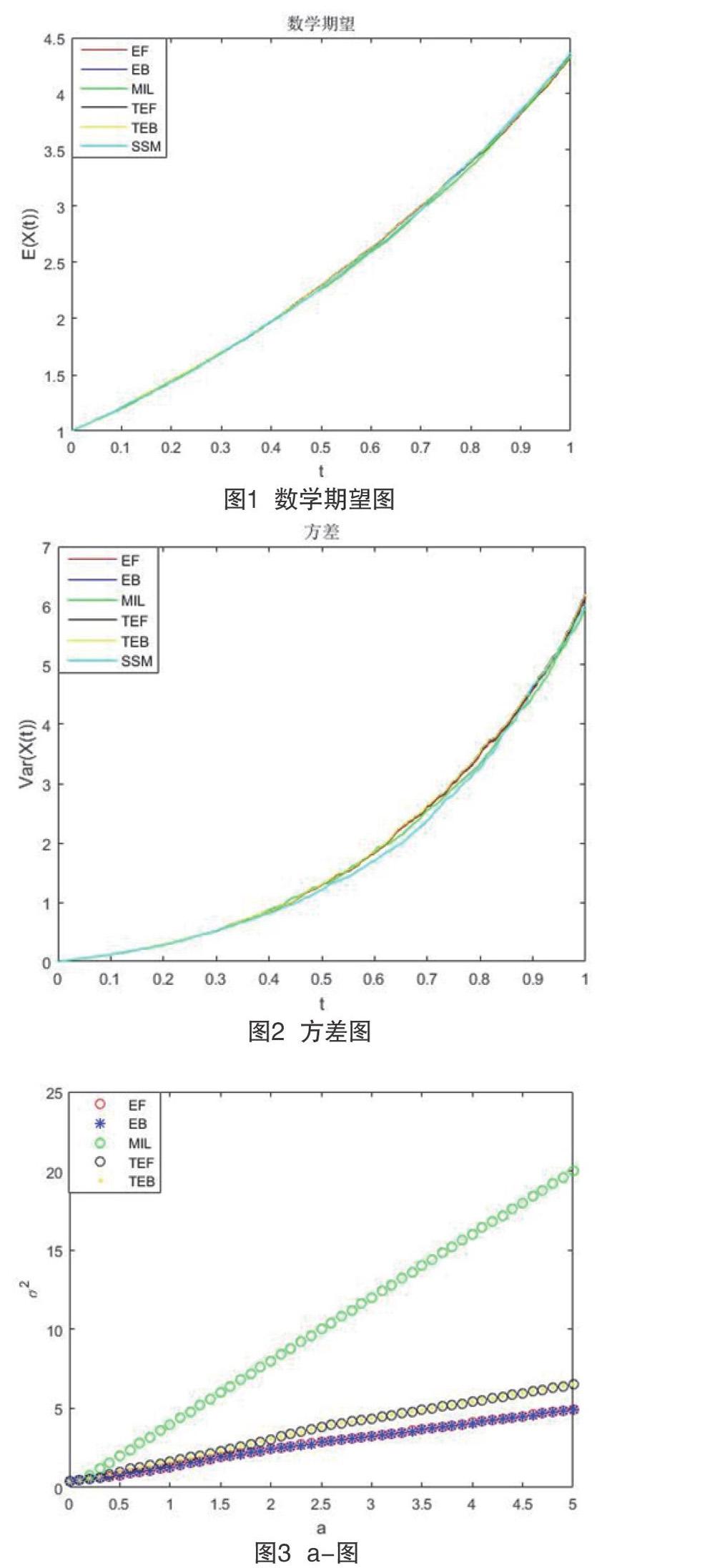
图1数学期望图：为简化表达，对算法进行缩写表示。以EF表示向前欧拉方法，以EB表示向后欧拉方法，以MIL表示Milstein方法，以TEF表示基于变换格式向前欧拉方法，以TEB表示基于变换格式向后欧拉方法，以SSM表示分裂步方法，此后图中均以缩写代表各方法。图中是各数值模拟方法得到的数学期望，横轴表示时间t且设置范围[0，1]，纵轴表示各时间对应的期望值E（X（t））。

计算各方法得到数值解的方差：

图2方差图：图中表示各数值模拟方法得到的方差，横轴表示时间t且设置范围[0，1]，纵轴表示各数值模拟方法在时间t的方差。

分析上述期望、方差可知，采用的数值模拟方法有效，得到的CIR模型（1.1）的数值解唯一，在统计特征上表现为同期望、同方差。

3  基于CIR模型算法的保正性及赋值分析

保正性在CIR模型的研究中是具有实际意义的，CIR模型主要描述短期利率的变化情况，利率在现实生活中的非负的;从CIR模型本身出发，在实数范围内，若为负数，模型扩散系数是没有意义的。故CIR模型严格要求保正，继而要求数值模拟时保正，则产生了对数值模拟方法保正性的研究需求。为解决数值模拟方法也就是相应的数值算法的保正性，需考虑两方面的问题：（1）是否存在绝对保正的数值算法;（2）对于存在不保正现象的算法，是否在满足某种条件下达到保正需要。基于这两个问题，将对第二部分中论述的数值算法进行分类，选出绝对保正的算法，对条件保正的算法进行条件强弱的比较。

由于CIR模型方程：中a、b皆为常数，且设置参数时要求为非负数，故模型中确定性部分对迭代过程的保正性始终起着正作用，而对于随机部分而言，白噪声项为标准的布朗运动，且有，在数值模拟过程中，利用蒙特卡洛模拟思想，以正态分布随机数模拟该随机过程，故存在小于0的随机数可能，使得模型随机部分对迭代过程保正性起着负作用。显然可知，首次出现负数只有一种情况，随机部分为负数，且绝对值大于确定性部分即：。换个思路，倘若a、b的数量级远大于是否就一定保正了呢？答案是肯定的，在要求a、b全为非负的前提下，令为0，则迭代过程中不可能出现负数的可能。这为研究绝对保正提供了一个思路，在的值远大于a、b的情况下，倘若算法还具有保正性，就可以说明其具有绝对保正性或者说严格保正。

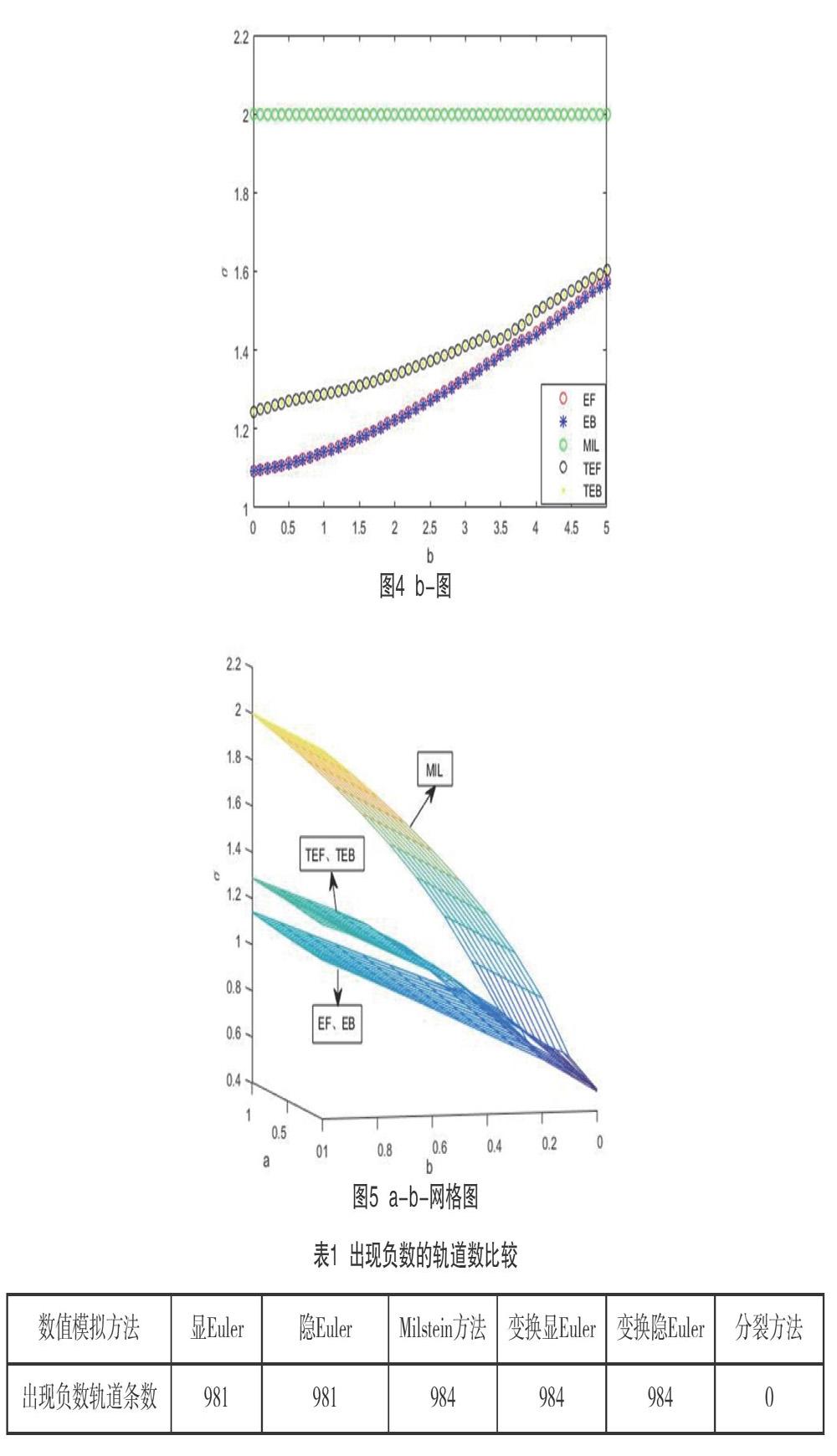
可知，存在一个充分小的实数，使得迭代过程一定保正，为探究各方法的保正性，不妨设置参数a=b=0，=5，初值，轨道数为1000，下表格为各迭代算法出现负数迭代步的轨道条数。

从上表可得，只有分裂方法对任意具有保正性。这是因为分裂方法利用卡方随机数进行模拟，而卡方随机数全为正数，故迭代步数值全为正数。

上述分析已经提及，当足够小时，数值模拟一定不会出现负数情况，即满足模型保正性要求，因此条件保正是一定存在的。定性分析是a、b越大，越小则满足保正性要求的可能性越大;定量分析是a、b、之间存在着某种关系时，算法在数值模拟中就一定保正。为进一步探究显隐式Euler方法、Milstein方法在参数a、b、满足什么条件下，会出现保正的情况，采用控制变量方法，单独研究a、b中一个参数与的关系：

情况1、固定b=1，内，发现各模拟方法中变量a与近似成正比。

图3，a-图：图中表示各数值模拟方法参数a与成正比关系，其中参数a为自变量且设置范围[0，5]，为因变量。

情况2、固定a=1，，绘制各模拟方法b与的曲线图，发现b与在各模拟方法中不存在明显的关系。

图4 b-图：图中表示各数值模拟方法参数b与之间的关系，其中参数b为自变量且设置范围[0，5]，为因变量，各方法间b-不呈现明显的关系。

情况3、设，得到各模拟方法a，b，关系三维网格图，分析各模拟方法的条件保正性。

图5 a-b-网格图：图中为各数值模拟方法参数a、b、三者之间的关系图，x轴为a，y轴为b，z轴为，其中参数a、b为自变量设置参数范围皆为[0，1]，为自变量。

分析上图可得：在曲面以下，算法保正，可知对任一平行于Z轴的直线，与曲面交点，Milstein方法的值最大，即根据值越小越保正的现象，Milstein方法在固定一组a、b值情况下，条件最弱。故Milstein算法的保正性最好，CIR方程变换格式的显隐式Euler方法次之，CIR方程基础格式的显隐式Euler方法的保正性最差。

参考文献

[1] Cox，J.C.，Ingersoll，J.E. and Ross，S.A. An intertemporal general equilibrium model of asset prices，Econometrica，1985（53）：363-384.

[2] Cox，J.C.，Ingersoll，J.E. and Ross，S.A. A theory of the term structure of interest rates，Econometrica，1985（53）：385-407.

[3] Kleoden P E，Platen E. Numerical Solution of Stochastic Differential Equations[M]. Berlin：Spring-Verlag，1992.

[4] Milstein G N. Approximate Integration of Stochastic Differential Equation [J]. Theor Prob Appl，1974（19）：557-562.