采用改进遗传算法的舰载机保障调度方法*

刘 珏，王能建，罗 旭，孟祥雷

(1. 哈尔滨工程大学 机电工程学院, 黑龙江 哈尔滨 150001； 2. 国防科技大学 装备综合保障技术重点实验室， 湖南 长沙 410073)

舰载机保障作业是保证舰载机顺利出动的必要环节[1]。由于航母甲板作业空间有限、海上气象条件的变化、保障设备及人员的变动，使得舰载机保障问题有着不同于陆基保障的特殊性。随着舰载机种类和数量的增加，以往依据经验制订保障计划的手工调度方法将难以满足未来战场的需求，而智能优化算法的发展为研究舰载机保障作业问题提供了新的思路。冯强等[2]利用多主体建模技术对有限资源下的舰载机保障调度进行了研究，通过仿真手段分析了特定故障率下固定架次的舰载机保障作业。王文秀等[3]以引进富余系数的排序论，对机务保障的资源配置优化进行了研究。栾孝丰等[4]在仿真模型中嵌入遗传算法，对多机机务保障进行研究并验证了该方法的有效性。李超等[5]论证了机务保障的模块化趋势，给出了其规划过程和符号描述，并通过设计结构矩阵(Design Structure Matrix, DSM)算法对模型求解，论证其提出方法的可行性。吕开东等[6]建立了舰载机航空保障的开环排队网络模型，从整体上分析了其在研究舰载机保障中的可行性。苏析超等[7]利用自适应变异策略和模拟退火机制对Memetic算法进行改进，将其运用于中、大规模的舰载机一站式保障调度研究。Michini等[8]利用逆向强化学习方法对舰载机舰面保障问题进行了研究，在需要同时对4架、8架舰载机同时保障的任务中分析比较了不同策略的优化方案。

上述研究内容多为单机或多机未考虑干扰因素的研究，对多机保障作业中含突发事件干扰的情况论述较少。因此，以不含干扰事件影响的调度方案为预设方案，以事件驱动策略与改进的遗传算法相结合对含干扰事件影响的调度方案进行优化。

1 舰载机保障作业调度问题数学模型

1.1 调度问题的描述

根据美国《海军航空部队航母训练标准手册》[9]公布的F/A-18E/F保障标准，总结了舰载机单机保障流程，见图1，单机保障作业时按流程图箭头指示顺序进行。然而，当同时有多架舰载机需要进行保障且保障组的数量有限时，将可能出现以下的资源受限情况[10-11]：①在原保障任务进行时，有舰载机退出或有新舰载机加入保障序列；②保障组数量较少而待保障的舰载机数量较多，或是保障组设备损坏而导致其不能参与保障；③多机保障时保障作业的调度方案不合理而导致部分舰载机的保障完成时间过长。发生以上情况都会对舰载机的持续作战能力产生影响，因此，需要综合考虑多机保障时资源受限情况对舰载机保障作业的干扰，并借助优化算法获得合理的保障作业调度计划，实时地对舰载机保障调度过程进行优化。

舰载机的保障作业问题与车间调度问题相类似，等待保障的舰载机可看作车间里待加工的工件，各类型保障组可看作是加工工件的机床，且有多个同类型机床可供选择，但不超过其待加工工件的总数。因此，关于舰载机的保障调度问题可描述为：有四种类别的保障组对舰面上n架飞机进行保障，且每架有m道保障工序需要四类保障组完成；这四类保障组分别完成图1所示的作业任务；其中，每道工序的作业时间固定，且均对应有Mq(q=1,2,3,4)个保障组。n架舰载机进入保障区，以相同的保障工序流程调用对应类型的保障组进行保障作业，但是，应满足如下假设条件。

1)保障作业具有连续性，每道保障工序作业中途不可停止，且只有保障完当前工序才可开始下一道工序；

2)各舰载机相互独立，各保障工序互不影响；

3)相邻两个工序的结束与开始的时间间隔忽略不计；

4)保障区内可完成上述保障工序，舰载机无须牵引车转运；

5)不考虑随机因素对保障过程的影响。

1.2 调度模型参数及变量定义

1)参数定义：

n为待保障的舰载机数量；m为舰载机保障工序数；Oij为表示第i架舰载机的第j个保障工序；M为保障组的总数量；Mq为可对工序Oij进行保障的某一类保障组集合，|Mq|为该类型保障组数量，其中1≤q≤4；Tijl为由第l(l≤M)个保障组对第i架舰载机的第j道工序的作业耗时；Bij为第i架舰载机的第j道工序开始时间；Dij为第i架舰载机的第j道工序结束时间；Pij为工序Oij的紧前工序集合；N为同时需要Mq类保障组的舰载机数量；Ci为第i架舰载机完成所有保障工序的耗时；Cmax为所有舰载机完成保障的最大耗时；Cijhk为保障组从第i架舰载机的第j道工序作业结束至第h架舰载机的第k道工序开始作业的转移耗时。

2)变量定义：

(1)

(2)

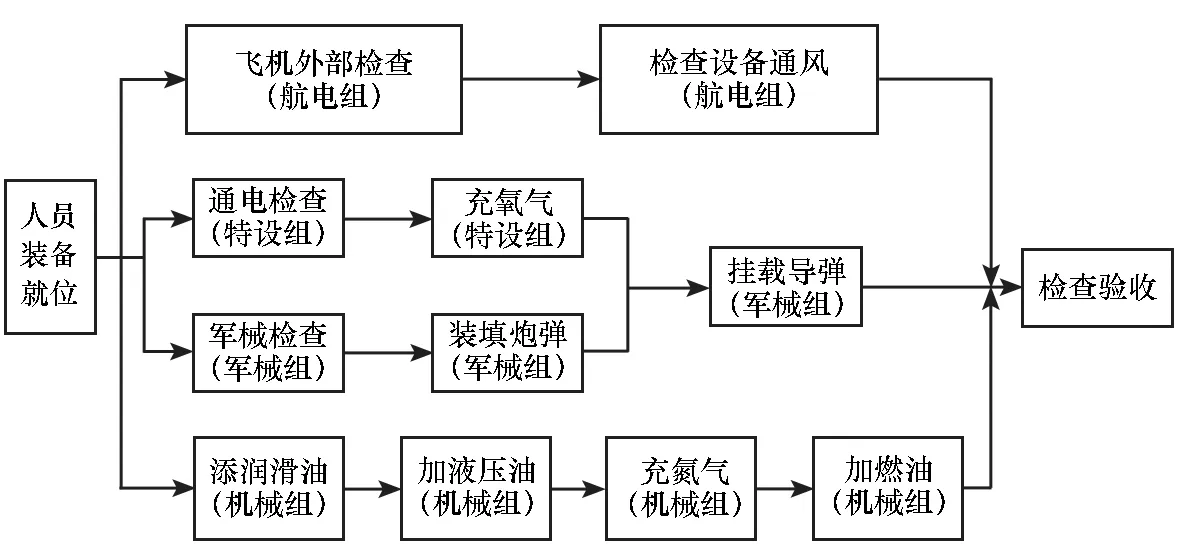
图1 舰载机单机保障流程图Fig.1 Flow chart of support operation of single aircraft

1.3 调度模型的建立

选取最大保障完成时间Cmax=max(Ci)作为优化目标,建立舰载机多机保障调度优化模型为：

F(x)=min(Cmax)

(3)

(4)

(5)

|Mq|≥1，1≤q≤4

(6)

(7)

(8)

max(Dih)≤Bij， 1≤i≤n,1≤j≤m,∀h∈Pij

(9)

Dij+Cijhk+R×βijhk≤Bhk+R1≤i,e≤n,1≤j,g≤m

(10)

N≤|Mq|

(11)

其中，式(3)表示调度优化的目标函数，即实现保障的最大用时最短；式(4)表示最大保障用时与舰载机保障工序用时和保障组移动用时的关系；式(5)表示舰载机的当前保障工序只能同时存在一个保障组作业，即完成该保障任务的保障组被占用，其值等于1；式(6)和式(7)表示各类型保障组中存在有一个或多个能完成相应保障工序的该类型保障组；式(8)表示任意舰载机的某一保障工序的作业时间关系；式(9)表示作业的紧前关系约束，即必须保证一个工序的所有紧前工序均保障结束后，此工序才能开始；式(10)表示同一保障组不能同时对不同的保障工序进行作业，且不同工序按优先级进行，式中R为足够大的实数，以保证不等式恒成立；式(11)表示同时作业的保障组不得超过该类型的最大数量。

2 改进型遗传算法设计

遗传算法(Genetic Algorithm, GA)是由Holland[12]提出的，它是一种能在搜索过程中自主学习和累积知识，并行生成多个个体，快速寻优的自适应算法。但是，其收敛过早、精度不高、易陷入局部最优的特点，影响了该算法在更多具有现实意义的复杂问题中的应用。因此，将遗传算法与禁忌搜索算法相结合有效地改善了其搜索过程，更有利于获得最优解，详见2.5节。

2.1 编码与解码

2.1.1 编码过程

对于舰载机保障调度问题，保障时有多架舰载机对应多个保障工序，因此，实数矩阵编码[13]恰好能直观地反映矩阵元素与舰载机及其保障工序之间的约束关系。该编码方式能够有效地搜索种群，获得最优调度方案，其形式如式(12)所示。

(12)

式中，矩阵Am×n，行表示舰载机待保障的工序序号，列表示不同舰载机的编号，元素aij是在区间(1, |Mq|+1)上的随机实数。其中，整数部分W(aij)表示第i架舰载机的第j道保障工序由第W(aij)个保障组负责完成；PoD(aij)(矩阵元素值的小数部分)的大小决定同一道保障工序在不同舰载机中的优先级。编码时将矩阵各行看作一段，各段以“0”分割，每段基因记载了不同舰载机的某一道保障工序的信息，因此，整个矩阵构成了一条含舰载机保障信息的长度为m×n+m-1的染色体：[a11,a12,…,a1n,0,a21,…，a2n,0,…,0,am1,…，amn]。

如下为区间(1, |Mq|+1)上随机生成的实数aij构成的编码矩阵：

其中，矩阵元素a11表示第一架舰载机的第一道保障工序由保障组1进行作业；矩阵元素a12表示第二架舰载机的第一道保障工序由保障组1进行作业，但由于其元素值1.6>1.3，因此，第二架舰载机的第一道保障工序的优先级高于第一架舰载机，保障组1需先对第二架舰载机进行保障；矩阵元素a13其值为2.4表示第三架舰载机的第一道保障工序由保障组2进行作业，其余元素释义依此类推。

2.1.2 解码过程

解码过程是实现编码染色体与保障调度方案的映射，同时，需充分考虑保障作业过程中的约束关系[14]。因此，将保障工序分成若干集合，以时序推进方式调动各保障工序所处集合，步骤如下。

设Ad为当前保障作业的工序集合，Cd为已完成保障作业的工序集合，Wl为未保障作业的工序集合，且随着时间推进，更新以上工序集合。

Step1：第i架舰载机进入保障站位，将其虚工序Bi的紧后工序PBi依据值W(aij)释放至相应的保障组序列。

Step2：工序Oij由第l个保障组保障，记录其开始时间Bij并更新集合。

Step3：记录工序Oij的保障结束时间Dij，将集合Ad中的元素转移到集合Cd，并判断Oij紧后工序的所有紧前工序PHij是否均已结束；若是，则释放紧后工序到对应保障组序列。根据PoD(aij)选取Wl中下一个保障工序，将其转移到集合Ad，并更新集合Cd。

2.2 初始种群与适应度函数

初始种群是由编码随机产生的若干染色体组成，通过适应度函数来评价个体的适应度值，且与目标函数的最大保障耗时有关，见式(13)。

(13)

其中，Cmax(k)表示第k个调度方案的最大保障耗时。

2.3 选择操作

父代个体适应度值的高低决定了子代个体被选择的概率，适应度值高，则被选中的概率大，反之，则个体被淘汰的概率大，因此，以轮盘赌法[15]选择子代个体，步骤如下：

Step1：求该染色体Vi(i=1，2，…，S)的适应度值eval(Vi)，其中，S表示群体的最大规模。

Step2：求群体的总体适应度值。

(14)

Step3：求染色体Vi(i=1，2，…，S)的被选概率：

(15)

Step4：由式(15)可知，染色体Vi(i=1，2，…，S)的累积概率为：

(16)

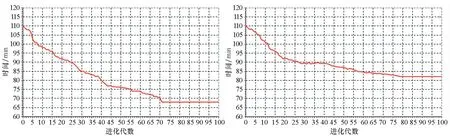
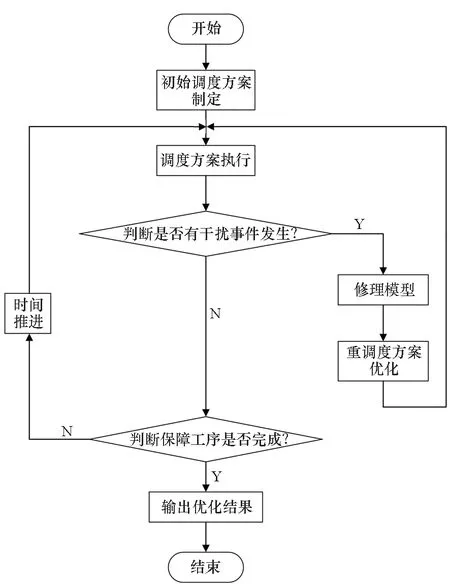
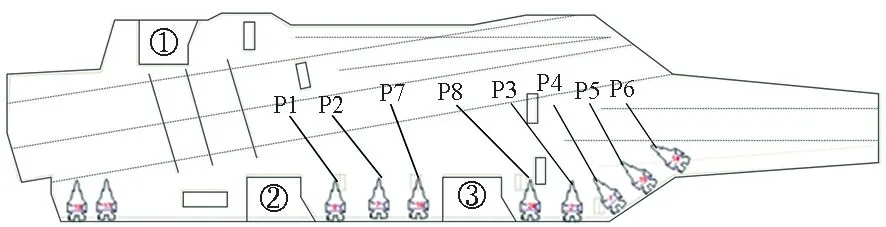
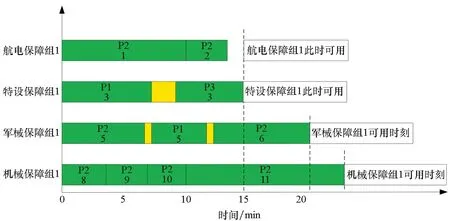
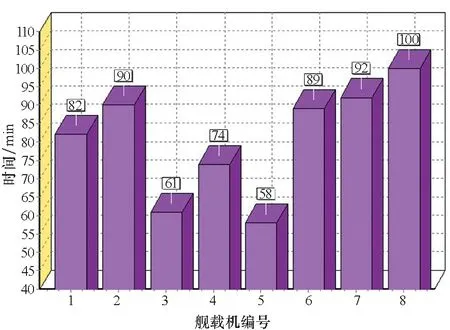
选择时每一轮将随机产生一个实数γ∈(0,1)，若指针落在第i个区间，其累积概率为p1+p2+…+pi-1<γ

图2 轮盘赌选择示意图Fig.2 Operation of selection with roulette

2.4 交叉操作

首先，按适应度值将若干染色体分组，一组为适应度值较高的染色体，其他的组成另一组。然后，从两组中分别随机地选取一条染色体交配，以此法形成新的一对个体，将使整个种群的适应度值向最优方向发展，具体的交叉操作如下所述。

将带有保障调度信息的染色体分段交叉，且每小段采用一点交叉(one-point crossover)法对两条染色体上同一位置的信息进行交换，从而确保串位后的两个个体携带的保障调度方案仍是可行的。例如，以A、B表示两个父代个体，在A、B上随机选择一处作为交叉点，如图3中箭头标记位置；然后，交换交叉点处的基因信息，从而获得子代A1、B1。

2.5 禁忌搜索下的变异操作

禁忌搜索(Tabu Search, TS)算法是由Glover等[16]提出的，它通过“禁忌表”的记忆方式引导搜索过程，避免陷入局部最优或重复过去的搜索。因此，将它与遗传算法相结合，使种群能高效地向优良方向繁衍。通过在不同迭代次数条件下调用禁忌搜索算子改进遗传算法搜索过程；观察改进算法的收敛效果，并截取遗传算法迭代第2至5次时调用禁忌搜索算子的收敛曲线，见图4。试验表明，以算法每迭代4次调用1次禁忌搜索的方式对遗传算法进行改进，在对保障作业的优化上效果最好。

图3 遗传算法的交叉过程Fig.3 Schematic diagram of crossover processing of genetic algorithm

(a) k=2 (b) k=3

(c) k=4 (d) k=5图4 不同迭代次数下调用禁忌搜索的优化曲线Fig.4 Optimized curve of tabu search with different number of iterations

因此，以k=4作为调用禁忌搜索算子的判断条件。若算法迭代次数k=4，则以禁忌算子进行变异操作，即在遗传算法框架中运用禁忌搜索算法进行变异操作，见图5。设定算法的迭代阈值，满足调用条件，则在交叉操作后用禁忌搜索算子对种群中每个个体的邻域进行搜索，生成候选集合；判断候选解是否为禁忌表中的对象，将最大搜索代数Gmax作为禁忌搜索的结束条件。

若k≠4，则采用传统变异算子进行变异操作，详述如下：

1)传统变异算子以变异概率Pm对交叉产生的种群随机反转其上某一位置的等位基因。

2)在染色体上随机选取变异位，依据如下：

①d=Rand{0,1}。

②若d=1，则r=Rand(0,|Mq|+1-aij)；否则r=Rand(0,aij-1)。

因此，改进遗传算法的实现步骤如下：

Step1：设定遗传算法基本参数，最大迭代次数Nd，初始群体规模Np，交叉概率Pc，变异概率Pm。

Step2：编码与解码设计，随机生成初始种群。

Step3：设计算法的适应度函数，计算种群中个体的适应度值。

Step4：按照轮盘赌规则进行遗传算法的选择操作。

Step5：按照2.4节中的交叉规则对选择后的个体进行交叉操作。

Step6：判断阈值是否满足k=4，若k≠4，则以传统变异算子进行变异操作，k=k+1，转至Step 8，否则，以禁忌变异算子完成变异过程。

Step7：调用禁忌变异算子进行变异操作：

①将遗传操作产生个体作为初始解，禁忌表设为空。

②判断是否满足停止准则，若满足，结束当前循环，重置阈值和禁忌搜索迭代次数，k=0，i=0；若不满足，继续以下步骤。

③从初始解x的邻域中选出符合禁忌要求的候选解。

④判断候选解是否满足期望，若满足，则转至⑦，否则继续以下步骤。

图5 禁忌搜索算子的变异操作流程Fig.5 Flow chart of tabu search operator in improved genetic algorithm

⑤判断候选解集中的解有无符合特赦准则要求的解，若符合，则将其特赦出来作为最优解，转至⑦；否则，继续以下步骤。

⑥当候选解不符合特赦准则要求，则在非禁忌对象中选出最优解。

⑦输出最优解。

⑧更新禁忌表，更新迭代次数ii=ii+1。

Step8：判断是否满足算法的结束条件，若满足，结束循环，否则，转至Step 3继续迭代，i=i+1。

3 舰载机保障作业仿真

3.1 模型修正策略

遇到干扰事件时，以如下策略对模型进行修正。

1)保障组可用时刻修正。舰载机保障作业过程遇到突发事件干扰，则需对保障调度方案进行重调度。此时，保障组的状态可能为“忙碌”“休息”。对于重调度方案中处于“休息”状态的保障组，重调度指令发出时刻即为该保障组的下一项作业开始时刻；对于重调度方案中处于“忙碌”状态的保障组，其作业过程具有连续性，应等待当前保障工序完成，并将该时刻作为重调度开始时刻。

2)舰载机保障工序矩阵状态修正。舰载机保障作业遇重调度时，除了需要确定保障组的工作状态是否可用外，还需要确定舰载机的保障状态，即舰载机保障作业是否完成，可分为“正在保障”“保障完成”。对于进入保障区的舰载机，其每一道保障工序都对应有这两个保障状态；若某舰载机的某一道保障工序的状态由“正在保障”变为“保障完成”，则将该道工序放入完工集合，并从工序矩阵中删除，保留未开始的保障工序。

3)保障设备工作状态修正。保障设备是否可用，既决定着保障组是否真正可用，也决定着舰载机保障工序的进程，因此，重调度发生时需确定各保障组保障设备的工作状态。当保障组设备故障时，应变更保障组状态为“不可用”，并从保障组的可用集合(休息、忙碌)中删除；正在作业的保障任务优先级高，需优先安排可用的“休息”保障组接替完成前序保障工序。

3.2 调度优化的仿真流程

在客观条件不具备的情况下，以模拟真实环境要素的仿真手段来检验改进型遗传算法对舰载机保障调度的优化效果是最为有效的途径，其流程见图6。

图6 仿真流程图Fig.6 Flow chart of simulation of carrier deck operation

步骤如下：

Step1：仿真开始后，算法给出关于当前舰载机保障的调度方案。

Step2：系统根据调度方案执行调度任务。

Step3：系统判断是否有干扰事件发生，干扰事件的分类详见1.1节，若无干扰事件影响，转至Step 6。

Step4：发生干扰事件，按3.1节所述规则对模型进行修正。

Step5：对修正后的模型给出调度方案，转至Step 2。

Step6：系统判断所有保障工序是否完成，完成则转至Step 8。

Step7：若保障工序未完成，则继续按时间顺序推进保障流程。

Step8：所有保障工序完成，则输出保障作业的甘特图。

4 案例分析

4.1 初始调度方案优化

以某波次舰载机保障作业为例，保障站位如图7所示，甲板“一站式”保障位上共有8架舰载机。其中，靠近③号升降机的两架舰载机已经战损(显示为红色)，无法在“一站式”保障位上维修，需要调入机库维修；对“一站式”保障位中其余6架舰载机进行保障，保障进行到第25 min时，由②号和③号升降机从机库各调出1架舰载机升至舰面保障区。案例中参与保障的各类保障组的数目为：2个航电保障组，2个特设保障组，3个军械保障组、3个机械保障组，其编号、作业内容、作业顺序、作业耗时，详见表1。将保障开始后的第25 min加入2架舰载机设为该案例的干扰事件，并在4.2节中详述。

图7 6架待保障的舰载机Fig.7 Six aircrafts of waiting support operation

如图6所示，仿真流程开始后，改进的遗传算法对甲板现有的6架舰载机进行保障作业的调度优化分析并执行其优化的调度方案。在无干扰的情况下，将按时间推进保障作业，最终输出优化结果，同时与传统遗传算法的优化结果做比较，算法及禁忌变异算子的初始参数设置如表2～3所示。仿真结束条件为最大迭代搜索次数100代。

表1 舰载机保障工序情况清单[17]Tab.1 List of support processing of aircraft

表2 遗传算法和改进型遗传禁忌算法主要参数Tab.2 Primary parameters of genetic algorithm and improved genetic algorithm

表3 禁忌变异算子主要参数表Tab.3 Primary parameters of mutation operator of tabu method

通过遗传算法和改进型遗传算法对舰载机的最大保障耗时进行优化和比较，其结果见图8。图中绿色曲线(GA)反映了遗传算法各代最优解的变化趋势，红色曲线(HGATS)反映了改进型遗传算法各代最优解的变化趋势。结果表明，改进型遗传算法在收敛速度以及优化舰载机保障作业时间上优于传统遗传算法。文献[1]中美军F/A-18舰载机出动回收保障时间一般在60～105 min(1+00～1+45 cycle)，而案例中6架舰载机的保障完成时间均小于75 min(1+15 cycle)， 见图9。

以保障组为主体观察仿真优化结果见图10，图中绿色块表示保障组“忙碌”，黄色块表示保障组在舰载机之间的转移耗时，空白处则表示保障组“休息”。色块中的字符Pi(i=1,2,3，…)表示正在保障的舰载机编号，Pi下面的数字表示正在保障的保障工序编号；横坐标表示保障组作业耗时，纵坐标表示各类保障组及此类保障组的编号。

以舰载机为主体观察仿真优化结果，见图11。横坐标表示舰载机保障耗时，纵坐标表示舰载机的编号。其中，绿色块内的字符Mij表示类型为i的保障组的第j个小组，M1表示航电类保障组，M2表示特种设备(简称：特设)类保障组，M3表示军械类保障组，M4表示机械类保障组。每架舰载机完成保障的耗时，见图8。

图8 算法改进前后的舰载机最大保障完成时间优化曲线Fig.8 Optimizing curve of maximum mission time of aircraft support operation before and after improved algorithm

4.2 重调度方案优化

如图6所示流程，当系统判断有干扰影响时，需对模型进行修正，然后，改进型遗传算法对初始调度方案进行再优化。如图12所示，在原保障方案执行第25 min时有两架舰载机(编号P7、P8)加入保障序列，对原保障过程形成了突发干扰。以图13为例说明遇干扰事件时的重调度过程，图中虚线分割的时刻(15 min)，航电组1与特设组1完成前序保障任务，处于“休息”，而军械组1与机械组1仍在“忙碌”，因此不可用。

图10 8架待保障的舰载机Fig.10 Eight aircrafts of waiting support operation

甘特图反映了舰载机各保障工序与保障组之间的任务分配关系。上述干扰事件发生时，各类保障组中，特设保障组1、军械保障组1和2、机械保障组1至3均处于“忙碌”状态，需待上述保障组完成当前作业后，方可加入重调度序列。因此，对比4.1节中6架舰载机的完成时间，8架舰载机的保障完成时间普遍要长，但仍然在单次出动回收的最大保障时间内(1+45 cycle)，见图14。第25分钟加入新的舰载机，需对模型修正后调用算法重调度，保障组甘特图如图15所示。可见，重调度优化后，航电组1、2，特设组2，军械组2、3以及机械组1的保障作业内容发生了变化。图16为各舰载机上进行的保障工序甘特图。

图11 6架舰载机优化调度方案保障组甘特图Fig.11 Gantt chart of optimizing scheduling plan of six aircraft′s support team

图12 6架舰载机优化调度方案舰载机甘特图Fig.12 Gantt chart of optimizing scheduling plan of six aircraft

图13 再调度保障组可用时刻Fig.13 Free time chart of support team of rescheduling

图14 8架舰载机的保障作业完成时间Fig.14 Support completion time of eight aircrafts

图15 8架舰载机优化调度方案保障组甘特图Fig.15 Gantt chart of optimizing scheduling plan of eight aircraft′s support team

图16 8架舰载机优化调度方案舰载机甘特图Fig.16 Gantt chart of optimizing scheduling plan of eight aircrafts

5 结论

根据舰载机保障作业特点，以改进遗传算法对舰载机保障作业中保障组的调度问题进行案例分析。在无干扰影响的初始保障调度方案优化中，对比了改进遗传算法和传统遗传算法的效果。结果表明，以引入禁忌搜索变异算子改进遗传算法来解决舰载机调度优化问题是可行的，且获得最优解的迭代次数及收敛效果要优于传统遗传算法。在干扰事件影响下，对某一时刻有新的舰载机加入保障序列的问题，以事件驱动机制对模型修正后，进行重调度优化，优化结果表明该算法仍能得到可行的最优解。上述案例仅是一种干扰事件在保障作业中的影响，随着仿真流程的循环及保障任务的推进，其他类型的干扰事件也可能发生，系统会根据具体事件制定新的重调度策略。案例表明，改进遗传算法能对干扰事件影响下的多机保障作业过程给出较为合理的调度优化方案，具有良好的鲁棒性和重要的研究意义。