面向作战任务的最小风险传感器调度方法*
2020-05-06单甘霖段修生
单甘霖,庞 策,段修生
(陆军工程大学 电子与光学工程系, 河北 石家庄 050000)
在现代化战争中,利用雷达、卫星、电子支援设备等传感器对目标进行探测预警成为作战开始的第一步。由于传感器资源有限,寻找一种有效的传感器管理方法,使传感器满足战斗需求的同时发挥最大效用,成为军事方面研究的热点和难点问题。
从1977年Nash采用线性规划的方法研究传感器管理问题开始,主要发展为三种基于贝叶斯理论的传感器管理方法:基于协方差的传感器管理方法[1-4]、基于信息论的传感器管理方法[5-8]、基于风险理论的传感器管理方法[9-12]。前两种方法虽然能够得到良好的技术指标,但尚未考虑实际作战需求,例如,在目标跟踪过程中,通过前两种方法可以得到较好的目标跟踪精度,但在不考虑发射导弹击中目标的情况下,若目标可能出现的位置分布在雷达波束范围内,即使目标跟踪精度较差,雷达波束也能探测到目标,此时,考虑目标跟踪精度失去了实际意义。而第三种方法紧密贴合作战任务建模,在考虑目标跟踪精度的基础上,进一步将不同跟踪效果产生的损失考虑到模型当中,以风险理论建模,使模型更具有实际意义,成为近几年学者关注的重点[13]。此外,进行传感器调度时必须紧密结合具体的作战任务,在不同作战任务的要求下,建立的传感器调度模型必然不同。
针对以上问题,本文提出一种面向作战任务的最小风险传感器调度方法。首先建立一般框架下的传感器风险管理模型,然后结合目标跟踪、目标识别、目标威胁等级评估三种不同作战任务将传感器风险管理模型具体化,接着针对模型求解提出改进人工蜂群算法,最后通过仿真验证证明模型和算法的有效性。
1 问题分析与建模

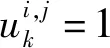
(1)
2 面向探测任务的传感器资源调度
2.1 面向目标跟踪的传感器资源调度
2.1.1 目标跟踪模型
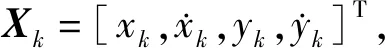

采用扩展卡尔曼滤波对目标状态进行估计,有:
(2)
其中,P为协方差矩阵,H为观测矩阵,Y为观测值,K为卡尔曼增益。
(3)

2.1.2 目标丢失概率模型
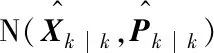
(4)
(5)
式中,Ω为波束beam照射区域。
2.1.3 目标丢失风险
2.2 面向目标识别的传感器资源调度
2.2.1 目标识别模型



(6)
2.2.2 目标识别错误风险

2.3 面向目标威胁等级评估的传感器资源调度
2.3.1 基于隐马尔科夫理论的目标威胁等级模型
在对目标威胁进行评估的过程中,通常用目标威胁度衡量目标威胁等级,但目标威胁度不能直接量测,一般为关于目标速度、位置、类型等的函数[16],而由于目标运动量测误差和模型误差,采用此方法得到的威胁度值通常存在一定误差。针对此问题,本文基于隐马尔科夫模型[17]建立目标威胁等级模型,以此避免量测误差和模型误差。目标威胁度等级定义为1(低等威胁)、2(中等威胁)和3(高等威胁),威胁度θ大小用威胁度等级信息状态矩阵E表征,在k时刻,有Ek=[ek(1),ek(2),ek(3)]T,其中,ek(i)=P(θk=i)。速度v分为1(低)、2(中)、3(高)三类,距离d分为1(近距离)、2(中等距离)、3(远距离)三类,攻击性c分为1(弱,假目标)、2(中,侦察机)、3(强,战斗机)三类。
在k时刻,目标的威胁等级按照状态转移矩阵3×3的A进行转移,其中ai,j=P(ek+1=j|ek=i)为k时刻目标威胁等级状态ek=i而k+1时刻ek+1=j的概率。
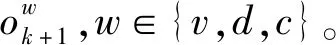
根据以上模型,给出k=0初始时刻目标威胁度的信息状态值E0,k+1时刻目标的威胁度信念状态可以通过如下方法进行估计:
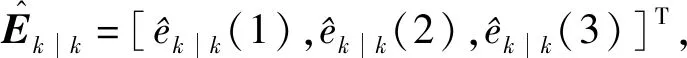
(7)

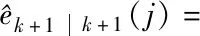
(8)
2.3.2 目标威胁等级评估错误风险
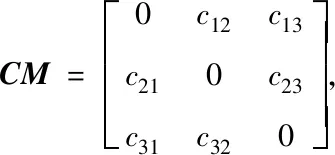
3 人工蜂群算法
人工蜂群算法是由土耳其学者Karaboga于2005年提出[18],具有操作简单、控制参数少、算法易实现等特点,其缺点是易陷入局部最优解。对此,本文提出改进人工蜂群算法。当采用蜂群算法求解传感器调度方案时,一个蜜源即一种传感器调度方案,由于该调度方案为0-1矩阵,在蜜源周围搜索时,产生新蜜源的方式可以看作是以该调度矩阵为基础生成新矩阵,且新矩阵与原有矩阵之间仅有少数元素不同,适应度为与“传感器调度目标函数”相关的函数。
3.1 基本人工蜂群算法
在基本人工蜂群算法中的公式如下所示。
1)蜜源生成公式为:
U=Umin+(Umax-Umin)rand
(9)
式中,U为可行解,Umin为可行解极小值,Umax为可行解极大值,rand∈[0,1]为任一随机数。
2)蜜源搜索公式为:
V=Uo+(Uo-Unear)φ
(10)
式中,V为被搜索的蜜源,Uo为当前所在蜜源,Unear为临近蜜源,φ∈[-1,1]为任一随机数。
3)蜜源适应度计算公式为:
(11)
式中,F(Uo)为蜜源Uo适应度值,F1(Uo)为Uo目标函数值。
4)跟随蜂按照轮盘赌选择引领蜂,有:
(12)
式中,P(Uo)为蜜源Uo被选概率,S为蜜源个数。
蜜蜂的种类共分为三种,即引领蜂、跟随蜂、侦察蜂, 各种蜜蜂的职能及算法步骤如下所示。
Step1:按照式(9)随机生成M个蜜源。
Step2:蜜源对应M个引领蜂,M个引领蜂按照式(10)对蜜源进行搜索并按照贪婪原则更新。
Step3:引领蜂对M1个跟随蜂进行招募,跟随蜂按式(11)、式(12)选择引领蜂,按照式(10)搜索并按照贪婪原则更新蜜源。
Step4:蜜蜂在同一个蜜源搜索达到top次时,蜜源质量依然未改善,则该处引领蜂变为侦察蜂,放弃现有蜜源,引领蜂按照式(9)生成新蜜源。
Step5:判断算法是否满足终止条件,若满足,则终止,输出最优解;若不满足,则回到Step2。
3.2 改进人工蜂群算法
为改善基本人工蜂群算法的寻优能力,提出两点改进措施:
1)用混沌理论对算法初始化。将混沌思想和反向学习思想用在可行解生成过程当中,在生成蜜源时采用混沌反向解策略,初始化蜜源过程中采用正弦迭代公式:
chnumber+1=sin(πchnumber)
(13)
U=Umin+(Umax-Umin)chnumber
(14)
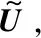
2)按照双向轮盘赌方式选择引领蜂。在选择引领蜂(Step3)时,除M1个跟随蜂按照式(11)、式(12)选择引领蜂外,同时另有M1个跟随蜂按照式(15)、式(16)选择引领蜂:
(15)
(16)
通过此措施,种群朝极大、极小两个方向进化,保存种群多样性,提高算法全局寻优能力。
4 仿真分析
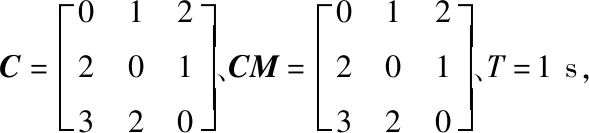
4.1 面向目标跟踪任务的传感器资源调度
4.1.1 多传感器—多目标配对仿真
在采用改进人工蜂群算法求解传感器调度方案时,对应第3节中的算法参数,取M=10、M1=50、top=10,总迭代次数设为50。
在k=0时刻,分别采用基本人工蜂群算法、改进人工蜂群算法、粒子群算法、遗传算法计算面向目标跟踪任务的多传感器—多目标分配方案,进行50次蒙特卡洛实验,取平均值,其计算过程如图2所示。
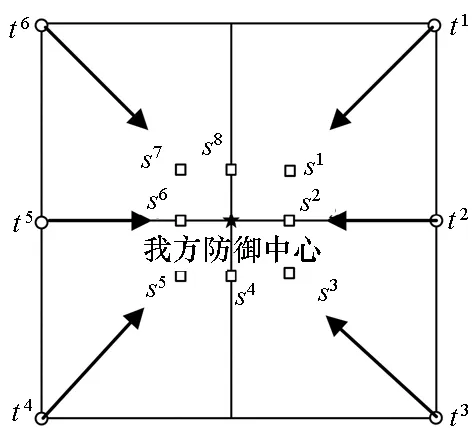
图1 作战态势Fig.1 Combat situation

图2 目标跟踪过程中算法迭代过程Fig.2 Computing process of algorithms in target tracking

表1 雷达性能参数Tab.1 Characters and parameters of radars
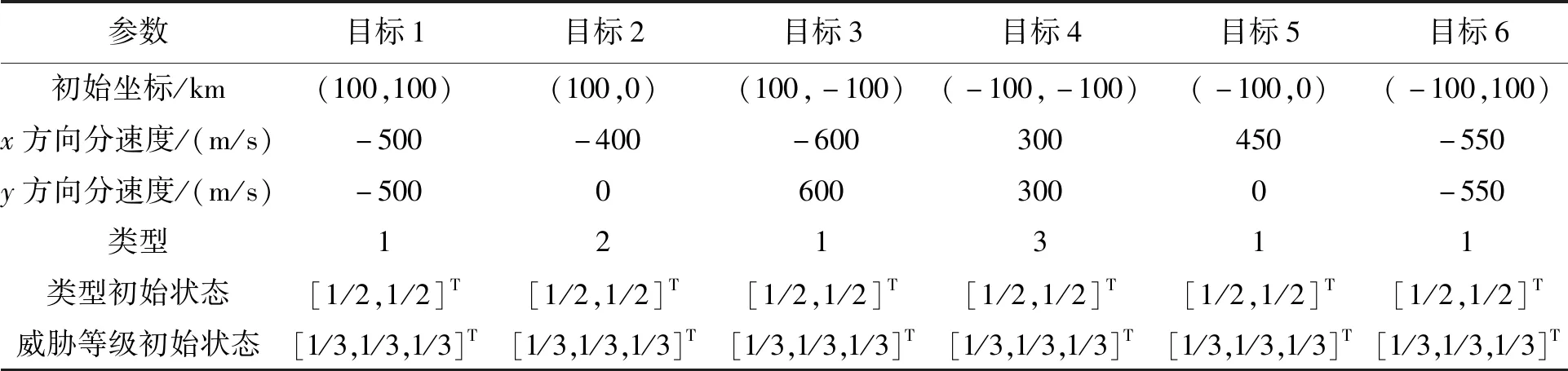
表2 目标参数Tab.2 Parameters of targets
由图2可知,与粒子群算法和遗传算法相比,基本人工蜂群算法虽然收敛速度较快,但易陷入局部最优解;而改进人工蜂群算法具有较快的收敛速度和较高的求解质量,能够顺利跳出局部最优解。采用改进人工蜂群算法计算传感器—目标配对方案,最终系统风险值为2.51,传感器与目标的对应关系为:s5—t1、s4—t2、s1—t3、s7—t4、s6—t5、s2—t6。
4.1.2 目标跟踪过程仿真

取α=0.5,目标函数是使传感器对目标跟踪后的信息增量最大。
分别采用本文提出的改进人工蜂群算法计算三种传感器管理方法生成的传感器管理方案对应的风险值以及目标跟踪精度,取30 s,其跟踪过程如图3所示。由图3(a)可知,通过本文传感器管理方法对目标进行跟踪,整个过程风险值最低;由图3(b)、图3(c)可知,本文方法得到的目标跟踪精度值高于跟踪精度控制以及信息增益控制得到的跟踪精度值,但目标丢失概率却与其他两种方法相差不大,其原因是,即使目标跟踪精度较差,但目标可能分布的位置在雷达波束照射范围内,目标的丢失概率依旧较低。
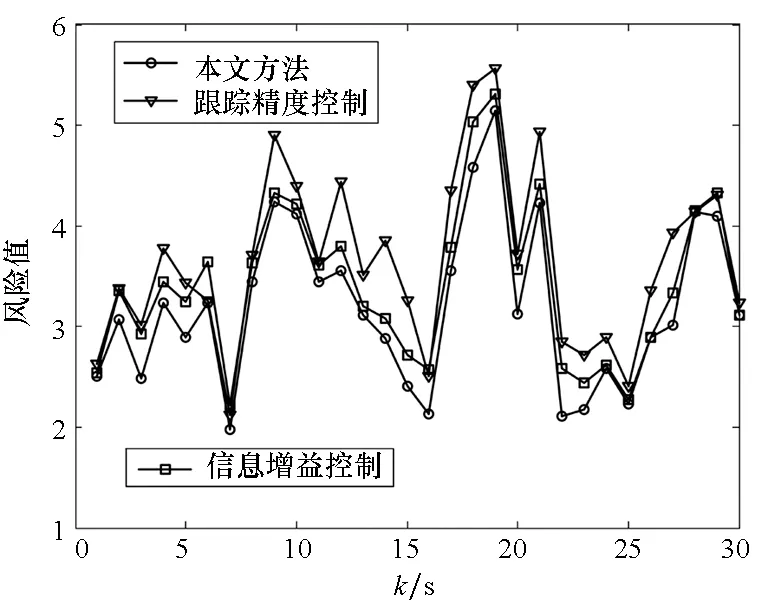
(a) 风险值随时间变化(a) Curves of the risk value varying with time

(b) 跟踪精度随时间的变化(b) Changes of tracking precision value varying with time

(c) 目标丢失概率(c) Target tracking loss probabilities图3 不同方法对比Fig.3 Comparisons of different methods
4.2 面向目标识别任务的传感器资源调度
4.2.1 多传感器—多目标配对仿真
在k=0时刻,分别采用基本人工蜂群算法、改进人工蜂群算法、粒子群算法、遗传算法计算面向目标识别任务的多传感器—多目标分配方案,进行50次蒙特卡洛实验,取平均值,其计算过程如图4所示。由图4可知,改进人工蜂群算法在计算面向目标识别任务时的传感器—目标配对方案时依然具有先进性。最终系统风险值为3.23,传感器与目标的对应关系为:s6—t1、s3—t2、s4—t3、s1—t4、s2—t5、s8—t6。

图4 目标识别过程中算法迭代过程Fig.4 Computing process of algorithms in target identification
4.2.2 目标识别过程仿真
采用本文提出的改进人工蜂群算法计算各个时刻风险值,并以目标t1、t2为例记录每个目标各个时刻的类型观测值、估计值,取10 s,其跟踪过程如图5所示。

(a) 风险值随时间变化曲线(a) Curves of the risk value varying with time
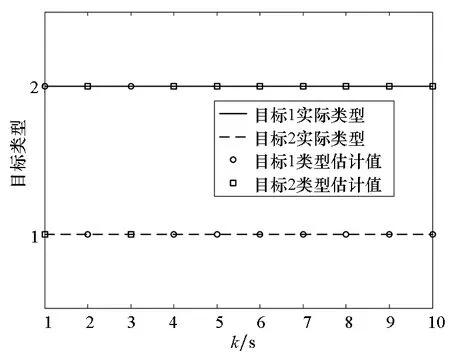
(b) 目标类型估计(b) Estimations of target′ classification图5 目标识别过程Fig.5 Process of target recognition
由图5可知,传感器对目标类型估计在初始时刻存在一定误差,但随着量测的增多,估计值趋于准确。由于目标类型属性为一个定值,没必要在整个目标探测过程中对目标一直保持识别,当对目标种类作出准确判断后即可停止识别。
4.3 面向目标威胁等级评估的传感器资源调度
4.3.1 多传感器—多目标配对仿真
在k=0时刻,分别采用基本人工蜂群算法、改进人工蜂群算法、粒子群算法、遗传算法计算面向目标威胁等级评估任务的多传感器—多目标分配方案,进行50次蒙特卡洛实验,取平均值,其计算过程如图6所示。
由图6可知,改进人工蜂群算法在计算面向目标威胁等级评估任务时的传感器—目标配对方案时性能较优。最终系统风险值为2.89,传感器与目标的对应关系为:s5—t1、s4—t2、s3—t3、s7—t4、s8—t5、s1—t6。
此外,图2、图4、图6表明,当对目标的探测任务不相同时,所求得的最优传感器—目标配对方案也不相同,传感器在进行调度时必须结合具体的作战任务。
4.3.2 目标威胁等级评估过程仿真
以目标t3为例,比较文献[16]与本文威胁评估方法的不同。在0~100 s内,目标威胁等级和威胁度随时间的变化如图7所示。
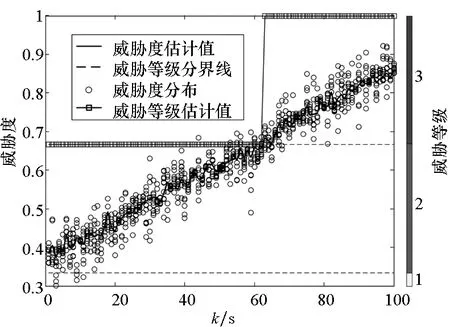
图7 威胁评估方法对比Fig.7 Comparisons of different threat-estimation methods
5 结论
本文提出了一种基于最小风险的传感器调度方法。首先建立一般框架下的传感器风险管理模型,然后分目标跟踪、目标识别、目标威胁等级评估三种情况将模型具体化。在模型求解过程中,提出基于混沌思想、反向学习思想和双向轮盘赌的改进人工蜂群算法。最后通过仿真实验证明了模型和算法的有效性。较之前研究成果相比,本文与实际情况连续更紧密,但结果的准确性受先验知识的影响,如何获取更准确的先验知识,将是论文进一步的研究方向。此外,基于风险的传感器调度方法也可为传感器资源不足情况下的调度问题提供一条新的解决思路,当传感器个数少于目标个数时,以最小风险为原则应舍弃对威胁度小的目标的跟踪,将传感器用于跟踪威胁度较高的目标,以此减小我方损失,此方法将在今后的实验中进一步论证。
