考虑非线性退化与随机失效阈值的剩余寿命预测*

2020-05-06王泽洲陈云翔蔡忠义罗承昆

国防科技大学学报 2020年2期

王泽洲，陈云翔，蔡忠义，罗承昆，2

(1. 空军工程大学装备管理与无人机工程学院，陕西西安 710051； 2. 北京系统工程研究所，北京 100101)

故障预测和健康管理(Prognostics and Health Management，PHM)是实现武器装备系统自主健康管理和综合维修保障的重要技术支撑，是提升战斗力的关键技术保证。作为PHM技术的核心，剩余寿命预测的精度与准确性将直接影响武器装备运行的可靠性与安全性，进而制约其作战效能的发挥。因此，如何实现对设备剩余寿命的准确预测，已成为近年来可靠性领域的研究热点。

目前，针对设备剩余寿命进行预测，主流研究多是基于随机过程展开，即认为设备的性能退化过程符合某种随机过程，例如逆高斯过程、伽马过程、Wiener过程，等等[1-5]。由于逆高斯过程和伽马过程必须严格单调，无法体现真实环境下广泛存在的非单调退化特征，因而制约了逆高斯过程与伽马过程的应用。为了实现对非单调退化过程的准确描述，Wiener过程开始被引入退化建模之中，并已逐步成为应用最为广泛的随机退化过程模型。Wiener退化过程，又可分为线性和非线性两类。由于线性Wiener过程是非线性Wiener过程的一种特殊形式，因此对非线性Wiener过程进行研究更具普遍意义，且在工程实践中应用也更加广泛。Kaiser等[6]提出了平均退化过程可线性化的假设，并运用对数变换的方法，将非线性Wiener过程转换为线性Wiener过程进行研究。基于上述假设，Wang[7]采用时间尺度变换法对非线性Wiener过程进行线性处理，进而建立退化模型。然而，线性化假设仅针对指数类型退化数据等有限类退化数据成立，难以满足普遍需要，因而制约了该类方法的应用。为了解决复杂非线性维纳退化过程难以建模的问题，Si等[8]采用时间-空间变换理论，将非线性Wiener退化过程达到固定失效阈值的用时问题转化为标准布朗运动的边界到达问题，进而推导出剩余寿命分布的近似表达式，实现了对非线性退化设备剩余寿命的预测。在此基础上，Tang等[9]进一步将设备间的个体差异与测量误差引入非线性Wiener退化过程，并推导出了考虑个体差异、测量误差以及非线性退化的设备剩余寿命概率密度函数解析表达式，进一步拓展了剩余寿命预测方法的应用范围。

然而，现有剩余寿命预测研究多是在失效阈值为固定值的条件下展开的[8-13]，并未考虑不确定失效阈值对设备剩余寿命预测的影响，这有可能会降低剩余寿命预测的准确性。设备失效阈值的不确定性主要源于生产制造过程中设备个体差异性以及使用过程中外界应力不确定性的共同作用，其直观体现的是设备的失效阈值难以用一个固定值来表述，例如弹簧的形变量、陀螺仪的漂移量、机械部件的磨损程度等[14-15]。Peng等[16]首次在退化建模过程中提出了不确定/随机失效阈值的概念，并分析了不确定/随机失效阈值对设备可靠性估计的影响，然而该研究并未给出失效阈值的具体分布类型与剩余寿命的解析表达。Usynin等[17]则基于线性Wiener过程讨论了累积损伤模型中随机失效阈值对设备可靠性估计的影响，但仍旧未能给出失效阈值的具体分布类型与剩余寿命的解析表达。Huang等[18]提出利用正态分布描述来描述随机失效阈值，并推导出了考虑随机失效阈值的设备可靠性积分表达式，但该研究并未给出随机失效阈值分布参数的估计方法，也未能给出剩余寿命预测研究中所需的剩余寿命分布解析式。

综上所述，现有针对随机失效阈值的研究仍存在三点不足：一是尚未针对非线性退化过程开展随机失效阈值的影响研究；二是针对随机失效阈值分布参数的估计方法研究尚不充分；三是尚未给出考虑随机失效阈值条件下设备剩余寿命概率分布的解析表达式。针对现有随机失效阈值相关研究存在的不足，本文基于非线性Wiener过程，分析随机失效阈值对设备剩余寿命预测的影响。本文的主要创新点有：①建立综合考虑个体差异与测量误差的非线性退化模型，并基于卡尔曼滤波原理对模型参数进行在线更新；②基于极大似然法提出随机失效阈值的分布参数估计方法；③推导出基于随机失效阈值的设备剩余寿命概率密度分布解析表达式。

1 非线性退化建模

理想状态下，基于Wiener过程的非线性退化模型可表示为:

X(t)=X(0)+λΛ(t,b)+σBB(t)

(1)

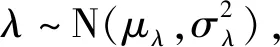
在实际运行环境中，由于存在外界噪声的干扰，设备真实的性能退化水平X(t)难以直接获取，利用状态监测手段仅能得到性能退化量的测量值Y(t)，而该测量值与真实值之间存在测量误差，即

Y(t)=X(t)+ε

(2)

2 随机失效阈值分布系数估计

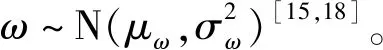
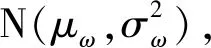
(3)

其中，Φ(·)为标准正态分布的累积分布函数。

本文利用极大似然法来估计随机失效阈值的分布系数。若有N个同类设备的历史失效数据ω={ω1,ω2,…,ωN}。则该类设备失效阈值ω对应的完全对数似然函数可表示为：

(4)

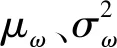
3 考虑随机失效阈值的剩余寿命预测

3.1 退化状态在线更新

对设备的退化状态进行在线更新，本质是基于状态监测数据Y(t)实现对设备退化状态X(t)与漂移系数λ的实时更新。依据式(1)与式(2)所示的Wiener退化过程，可得如下状态方程：

(5)

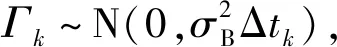
考虑到Wiener过程假设同一退化过程中不同阶段对应的漂移系数不变，易得λk=λk-1，由此可利用卡尔曼滤波原理构建设备退化状态的更新机制，如式(6)所示。

(6)

假设Y1 ∶k=(y1,y2,…,yk)T与X1 ∶k=(x1,x2,…,xk)T分别表示t1,t2,…,tk时刻设备性能退化的测量值与真实值。首先定义状态变量Zk的期望和方差分别为：

(7)

(8)

同理，可将状态变量Zk进一步估计的期望和方差定义为：

(9)

(10)

基于上述分析，运用卡尔曼滤波对隐含状态xk和λ进行同步更新，具体过程如下：

(11)

(12)

Pk|k=Pk|k-1-ψkCPk|k-1

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

易知初始值为：

(22)

(23)

利用式(11)～(23)，即可实现对退化状态的在线更新。

3.2 剩余寿命预测模型

设备的寿命通常被称为首达时间(First Hitting Time，FHT)，即设备的性能退化量首次达到失效阈值的时间。用ω表示性能退化的失效阈值，则设备的寿命T可表示为：

T=inf{t∶X(t)≥ω|X(0)<ω}

(24)

对于满足非线性Wiener退化过程的设备，可知其寿命T近似服从逆高斯分布，且寿命T对应的概率密度函数(Probability Density Function, PDF)可近似表示为[8]：

(25)

若令lk表示设备在tk时刻对应的剩余寿命，则可得T=lk+tk。进而可将tk时刻设备对应的剩余寿命定义为：

L=inf{lk∶X(tk+lk)≥ω|X(0)<ω}

(26)

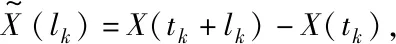
(27)

其中，ψ(lk)=Λ(tk+lk,b)-Λ(tk,b)。

(28)

假设失效阈值ω为固定值，基于式(25)与式(28)，可推导出非线性退化设备剩余寿命概率分布的解析式，如式(29)所示。

fLk|ω,λk,X1 ∶k(lk|ω,λk,x1 ∶k)

(29)

其中：β(lk)=ψ(lk)-(dψ(lk)/dlk)。

由前文分析可知，设备的随机失效阈值满足截断正态分布。为了推导考虑随机失效阈值条件下设备剩余寿命的概率密度函数，本文给出定理1。

定理1若D～TN(μ,σ2),E,F∈R,G∈R+,则

(30)

定理1的证明过程可由文献[10]中引理1的证明过程经变形扩展得到，在此不做详细证明。

进一步分析可得：

fLk|ω,λk,Y1 ∶k,X1 ∶k(lk|ω,λk,Y1 ∶k,X1 ∶k)

=fLk|ω,λk,X1 ∶k(lk|ω,λk,X1 ∶k)

(31)

基于全概率公式，若Y1 ∶k已知，则考虑随机失效阈值条件下设备的剩余寿命可表示为：

fLk|Y1 ∶k(lk|Y1 ∶k)

p(xk|λk,ω,Y1 ∶k)p(λk|ω,Y1 ∶k)·

p(ω|Y1 ∶K)dxkdλkdω

=Eω(Eλk|ω{Exk|ω,λk[fLk|ω,λk,X1 ∶K(lk|ω,λk,X1 ∶k)]})

(32)

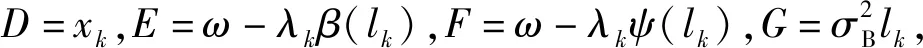
fLk|ω,λk,Y1 ∶k(lk|ω,λk,Y1 ∶k)

=Exk|ω,λk[fLk|ω,λk,X1 ∶k(lk|ω,λk,X1 ∶k)]

(33)

其中

(34)

(35)

(36)

fLk|ω,Y1 ∶k(lk|ω,Y1 ∶k)

=Eλk|ω{fLk|ω,λk,X1 ∶k(lk|ω,ωk,X1 ∶k)}

(37)

其中

(38)

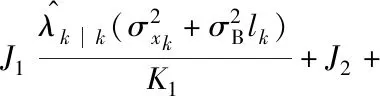
(39)

(40)

(41)

基于式(37)与定理1，并令D=ω，F=K4，E=K2/K3，G=K1，可得：

fLk|Y1 ∶k(lk|Y1 ∶k)

=Eω[fLk|ω,Y1 ∶k(lk|ω,Y1 ∶K)]

(42)

基于上述分析可得，考虑随机失效阈值条件下设备剩余寿命的期望与可靠度分别为：

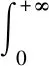
(43)

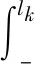
(44)

4 算例研究

4.1 仿真数据分析

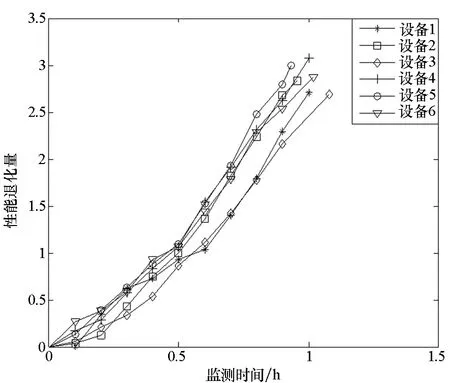
图1 仿真退化数据Fig.1 Simulation degradation data

为便于对比分析，记M0为本文所提剩余寿命预测方法；令M1表示文献[9]提出的仅考虑非线性退化的剩余寿命预测方法；而令M2表示仅考虑随机失效阈值的剩余寿命预测方法(即令M0中Λ(t,b)=tb的参数b=1)。基于上述仿真数据，针对M0、M1、M2所描述的性能退化模型，采用极大似然法分别对其进行参数估计，得到退化模型的参数估计值，具体情况详见表1。

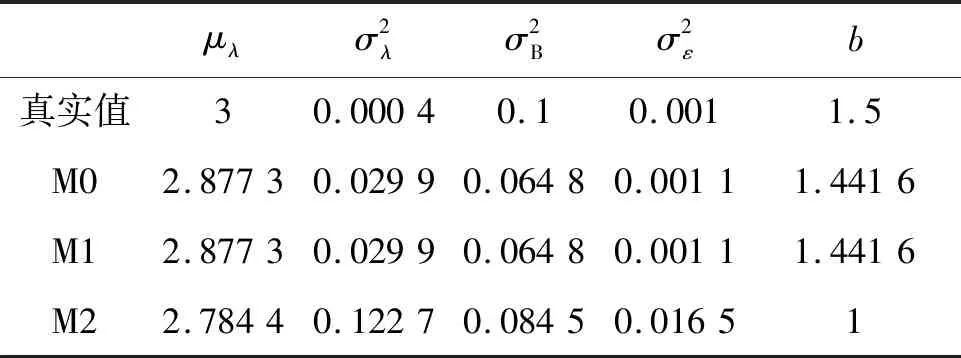
表1 退化模型参数估计值Tab.1 Parameter estimation value of degradation model

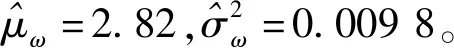
由表1可知，M0与M1较M2的参数估计值更接近于真实值，这表明M0与M1较M2的模型拟合性更好。为了直观体现本文所提方法的优势，引入均方误差(Mean Squared Error, MSE)作为衡量模型拟合性的判定标准，MSE值越小，表明模型拟合性越好，方法越准确。MSE的具体表达式为：

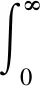
选取区间[0.2 h,0.9 h]，分别计算M0、M1与M2对应的MSE值，如图3所示。

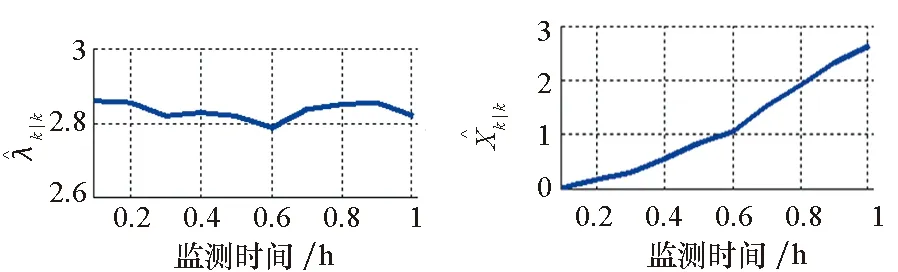
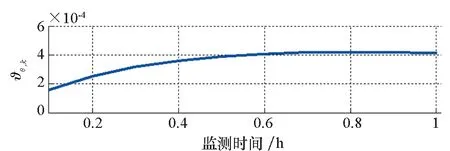
图2 退化状态更新Fig.2 Degradation status updating

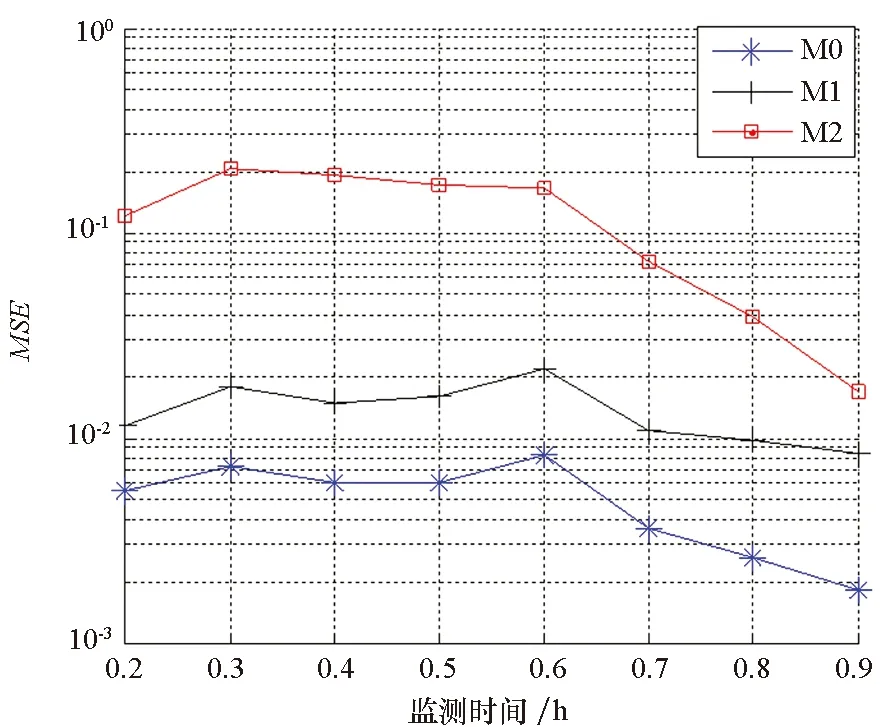
图3 M0、M1、M2的MSEFig.3 MSE under M0, M1 and M2

由图3可知，M0的MSE值低于M1，更低于M2，这表明M0中构建的退化模型较M1与M2更贴近实际，说明了本文所提方法在模型拟合性上较现有方法更具优势。

为了进一步分析比较M0、M1与M2在剩余寿命预测准确性与精度方面的差异，基于仿真数据，运用M0、M1与M2分别求解出设备剩余寿命的概率密度函数，具体如图4所示。

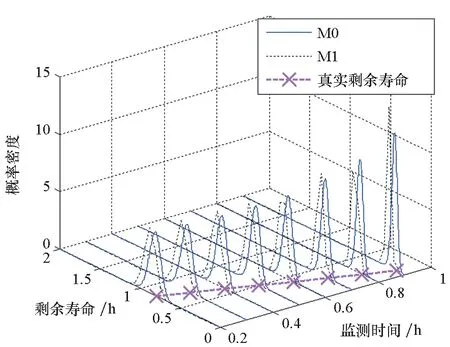
(a) M0、M1

(b) M0、M2图4 M0、M1、M2对应的设备剩余寿命概率密度函数Fig.4 PDF of RUL under M0, M1 and M2

由图4可知，在不同状态监测时刻，M0与M2得到的剩余寿命PDF均可覆盖目标设备的真实剩余寿命，而M1得到的剩余寿命PDF无法做到对目标设备剩余寿命的全覆盖，这表明M1对剩余寿命预测的准确性要低于M0与M2。为了对比M0与M2的差异，本文给出M0、M1与M2在tk=0.9 h时刻对应的设备剩余寿命概率分布情况，如图5所示。

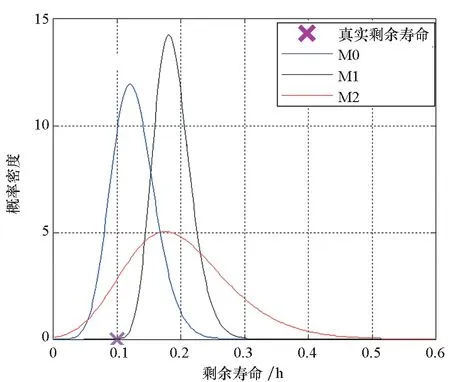
图5 0.9 h时刻M0、M1、M2对应剩余寿命概率密度函数Fig.5 PDF of RUL under M0, M1 and M2 at 0.9 h

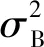
图6给出了M0、M1与M2对应设备剩余寿命的95%置信区间。由图6可知，M0和M2对应剩余寿命的95%置信区间均可完全包含目标设备的真实剩余寿命，而M1对应的置信区间则无法完全包含目标设备的真实剩余寿命，从而进一步证明了M1对剩余寿命预测的准确性不及M0和M2。此外，相较于M2的剩余寿命置信区间，M0对应置信区间的宽度更窄，再次证明了M0具有更高的剩余寿命预测精度。

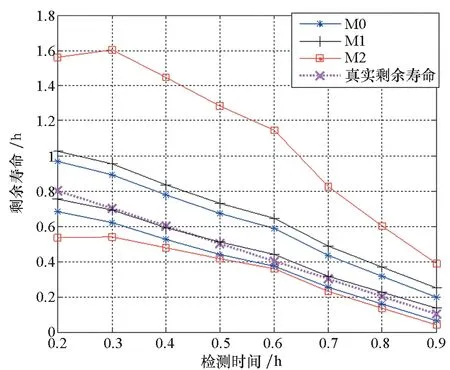
图6 M0、M1、M2对应设备剩余寿命95%置信区间Fig.6 95% confidence intervals under M0, M1 and M2

为分析仿真样本数量对剩余寿命预测结果的影响，基于仿真退化参数，本文分别仿真出6、60、600台设备的性能退化数据。并通过引入赤池信息量准则(Akaike Information Criterion, AIC)来衡量样本数量对剩余寿命预测结果的影响，其中AIC的定义式如下：

AIC=2[k-ln(-LF)]

AIC值越小，表明退化模型越贴近于实际退化过程，剩余寿命预测精度越高；反之，则越不能反映真实退化规律，预测精度越差。

表2给出了在不同样本数量下，M0对应的退化模型参数估计值与AIC值。通过分析可以发现，随着仿真样本数量的提升，退化模型参数估计值越接近初始仿真参数(即真实值)，且AIC值越小。表明通过增加仿真样本数量，有助于进一步提高退化模型参数估计的准确性以及剩余寿命的预测精度。然而在实际使用过程中，性能退化模型多应用于高可靠、长寿命或新研设备，出于成本和现实条件的制约，退化试验中该类设备的样本数量往往较少，导致预测误差难以避免。

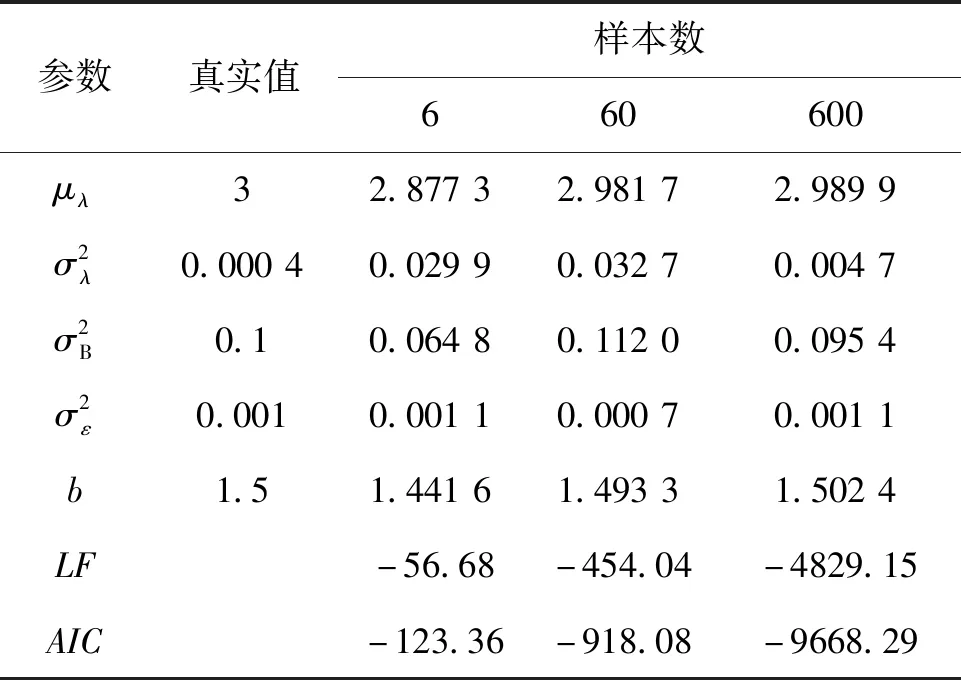
表2 仿真数据对比(M0)Tab.2 Simulation data comparison (M0)

4.2 铣刀退化数据分析

铣床是机械加工中广泛使用的一种机床，其通过自身携带的铣刀对工件进行加工，进而得到满足要求的铣削件。受工作条件与加工材料的影响，铣刀在使用过程中会发生磨损现象，进而影响其铣削性能，严重时将导致失效。通常情况下，可将铣刀的后刀面磨损(VB)作为铣刀性能退化的特征量进行分析。本文基于文献[19]给出的某型铣刀的退化试验数据进行分析，其中铣刀的切削深度为0.75 mm，进刀量为0.5 mm/r，切削材料为铸铁，对应退化轨迹如图7所示。

图7 铣刀退化数据Fig.7 Milling degradation data

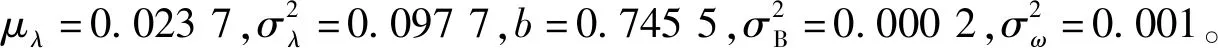
基于铣刀磨损数据可得M0、M1与M2预测的铣刀剩余寿命分布情况。本文以1号铣刀第59次铣削后的剩余寿命分布情况为例进行说明，如图8所示。由图8可知，铣刀对应的真实剩余寿命为lk=72-59=13次，其中M0与M2对应的剩余寿命概率密度函数均可包含铣刀的真实剩余寿命，而M1对应的剩余寿命概率密度函数无法包含其真实剩余寿命，且M0较M2具有更窄的概率密度函数，表明M0较M1与M2在预测准确性与精度方面更具优势。该结论与仿真分析结果相一致，进一步证明了本文所提方法的科学性与有效性。